LeetCode 741 动态规划-详细解析 + 图解

解题思路
按照题意，一个人来回走两趟，必定在地图上留下两条路径。
我们可以想象有两个人，AA 和 BB，同时从点 (0,0)(0,0) 出发。
每一次移动，两个人同时移动一步（向右或向下）。
容易证明，每次移动后，两个人必定在同一条对角线上。
如果某次移动后，两个人在同一位置，则最多只能摘得一个樱桃。
最终，两个人都会移动到点 (N-1,N-1)(N−1,N−1) 上，留下两条路径。这两条路径所摘得樱桃数，即为题目所求。

先上图，思路在后面解释：

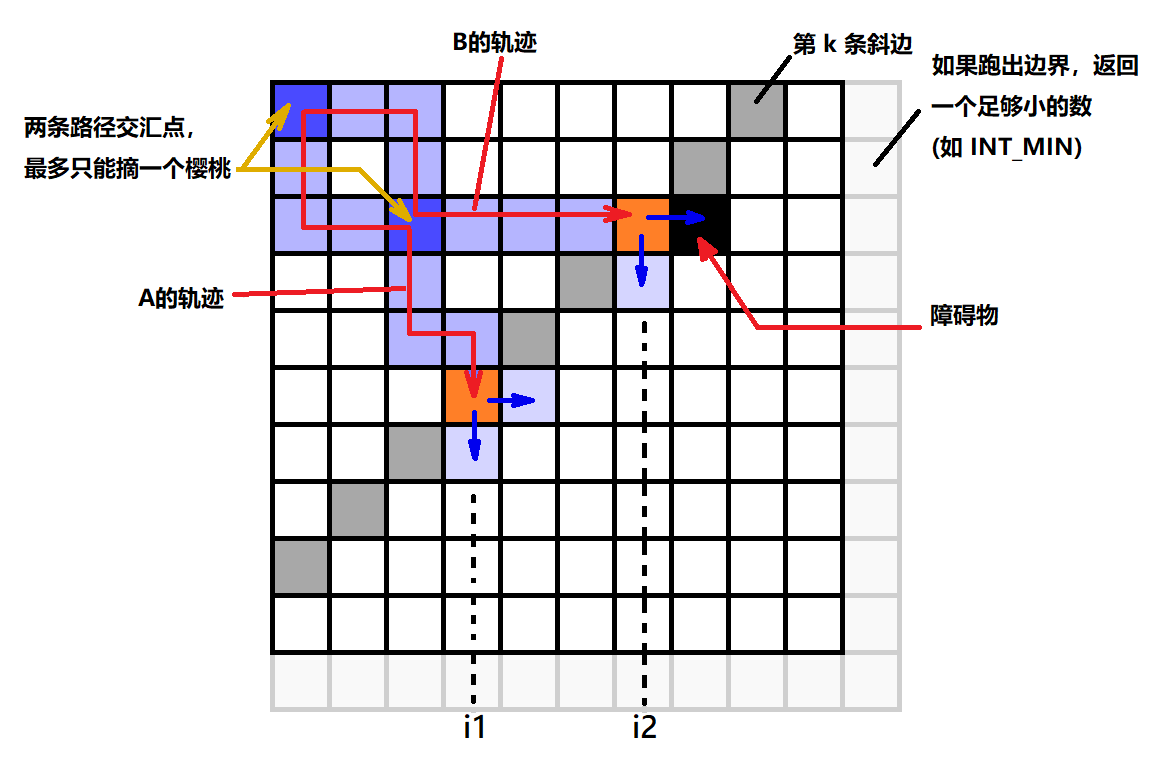
首先可以得到一个比较简单的动态规划思路。

代码
20~24 ms

class Solution {
public:
int cherryPickup(vector<vector<int>>& grid) {
int N = grid.size(), dp[N+1][N+1];
memset(dp, 0x80, sizeof(dp)); //-2139062144, 作用相当于 INT_MIN
dp[N-1][N-1] = grid[N-1][N-1]; // 初始边界条件
for(int sum = 2*N - 3; sum >= 0; --sum)
for(int i1 = max(0, sum - N + 1); i1 <= min(N-1,sum); ++i1)
for(int i2 = i1; i2 <= min(N-1,sum); ++i2)
{
int j1 = sum - i1, j2 = sum - i2;
if(grid[i1][j1] == -1 || grid[i2][j2] == -1)
dp[i1][i2] = INT_MIN;
else
dp[i1][i2] = grid[i1][j1] + (i1 != i2 || j1 != j2)*grid[i2][j2] + max(
max(dp[i1][i2+1], dp[i1+1][i2]),
max(dp[i1+1][i2+1], dp[i1][i2])
);
}
return max(0, dp[0][0]);
}
};

java版本:

import java.util.Arrays;

class Solution {
    public int cherryPickup(int[][] grid) {
        int N = grid.length;
        int[][] dp = new int[N + 1][N + 1];
        for (int[] row : dp) {
            //使用了N+1的大小，因此边界值也设置为MIN_VALUE
            Arrays.fill(row, Integer.MIN_VALUE);
        }
        //动态规划涉及方向，此题倒序来找
        dp[N - 1][N - 1] = grid[N - 1][N - 1];

        //sum表示一共要走的步数，也就是k，通过一个循环递增，来降低一个维度，从而不需要使用三维数组k那一维,
        //当前走第sum步，一共要走2*N-2步（n-1）*2,下标的话就是2N-3，注意是倒序的
        for (int sum = 2 * N - 3; sum >= 0; sum--) {
            // i1的起始值范围，如果对角线在正方形左上部分，就是0;如果在右下部分，因为此时起点的纵坐标是N-1，所以横坐标就是总步数sum - (N - 1),也就是sum - N + 1
            for (int i1 = Math.max(0, sum - N + 1); i1 <= Math.min(N - 1, sum); i1++) {
                for (int i2 = i1; i2 <= Math.min(N - 1, sum); i2++) {
                    //i1、j2的关联：一共要走sum步，sum<2*n，因此起点为Math.max(0,sum-N+1),限定了i1的范围，因此 j1 = sum -i1 = sum - (sum-n+1) = n-1,也就是当i1取最大，j1的下标也只能为n-1
                    //i2的优化：从i1开始计算，表明第二个人一定走在i1的下面
                    int j1 = sum - i1;
                    int j2 = sum - i2;
                    if (grid[i1][j1] == -1 || grid[i2][j2] == -1) {
                        //遇到荆棘
                        dp[i1][i2] = Integer.MIN_VALUE;
                    } else {
                        if (i1 != i2 || j1 != j2) {
                            //不重合在同一个点，则获取的最大值=A的格子+B的格子+AB往哪个方向走，也就是上一个状态是怎么来得，
                            dp[i1][i2] = grid[i1][j1] + grid[i2][j2] + Math.max(Math.max(dp[i1][i2 + 1], dp[i1 + 1][i2]), Math.max(dp[i1][i2], dp[i1 + 1][i2 + 1]));
                        } else {
                            //重合在一个点，grid[i1][j1] == grid[i2][j2]，取一个即可，后面是4个方向
                            dp[i1][i2] = grid[i1][j1] + Math.max(Math.max(dp[i1][i2 + 1], dp[i1 + 1][i2]), Math.max(dp[i1][i2], dp[i1 + 1][i2 + 1]));
                        }
                    }
                }
            }
        }

        return Math.max(0,dp[0][0]);
    }
}

LeetCode 741 动态规划-详细解析 + 图解

猜你喜欢