生成式对抗网络的基本原理
场景描述
生成式对抗网络(Generative Adversarial Network,GAN)一般由两个神经网络组成,一个网络负责生成样本,另一个网络负责鉴别样本的真假,这两个网络通过“相爱相杀”的博弈,一起成长为更好的自己。这种简洁优美的生成方法背后的数学原理却并不是这么直观。本节将从初始版本的GAN出发,通过学习GAN的原理,对比GAN与其他几种生成式模型的异同,以及分析原始GAN中存在的问题,以获得对GAN的深度理解。
知识点
生成模型、自编码器(AutoEncoder, AE)、变分自编码器(Variational AutoEncoder, VAE)、模式坍塌(mode collapse)、收敛性
问题1 简述AE、VAE、GAN 的联系与区别。
难度:★★★☆☆
分析与解答
近年来,采用神经网络的生成式建模方法逐渐成为生成模型的主流。AE、VAE和GAN同属于可微生成网络,它们常常用神经网络来表示一个可微函数
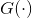
,用这个函数来刻画隐变量
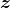
到样本分布的映射关系。通过分析这3种模型的联系与区别,我们可以更加清晰地了解它们的特质。首先来看这3种模型各自的特点。
■自编码器(AE)
标准的AE由编码器(encoder)和解码器(decoder)两部分组成,如图5.1所示。整个模型可以看作一个“压缩”与“解压”的过程:首先编码器将真实数据(真实样本)
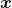
压缩为低维隐空间中的一个隐向量
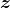
,该向量可以看作输入的“精华”;然后解码器将这个隐向量
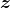
解压,得到生成数据(生成样本)
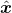
。在训练过程中,会将生成样本
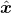
与真实样本
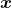
进行比较,朝着减小二者之间差异的方向去更新编码器和解码器的参数,最终目的是期望由真实样本

压缩得到的隐向量
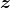
能够尽可能地抓住输入的精髓,使得用其重建出的生成样本
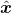
与真实样本
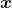
尽可能接近。AE可应用于数据去噪、可视化降维以及数据生成等方向。
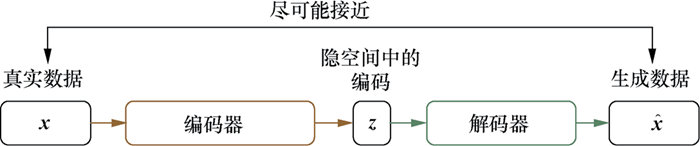
图5.1 自编码器(AE)的基本框架
■变分自编码器(VAE)
VAE是AE的升级版本,其结构也是由编码器和解码器组成,如图5.2所示。AE在生成数据时只会模仿而不会创造,无法直接生成任意的新样本,这是因为AE在生成样本时用到的隐向量其实是真实样本的压缩编码,也就是说每一个生成样本都需要有对应的真实样本,AE本身无法直接产生新的隐向量来生成新的样本。作为AE的重要升级,VAE的主要优势在于能够产生新的隐向量
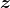
,进而生成有效的新样本。VAE能够生成新样本(即VAE与AE的最大区别)的原因是,VAE在编码过程中加入了一些限制,迫使编码器产生的隐向量的后验分布
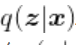
尽量接近某个特定分布(如正态分布)。VAE训练过程的优化目标包括重构误差和对后验分布
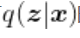
的约束这两部分。VAE编码器的输出不再是隐空间中的向量,而是所属正态分布的均值和标准差,然后再根据均值与标准差来采样出隐向量
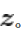
。由于采样操作存在随机性,每一个输入图像经过VAE得到的生成图像不再是唯一的,只要

是从隐空间的正态分布中采样得到的,生成的图像就是有效的。
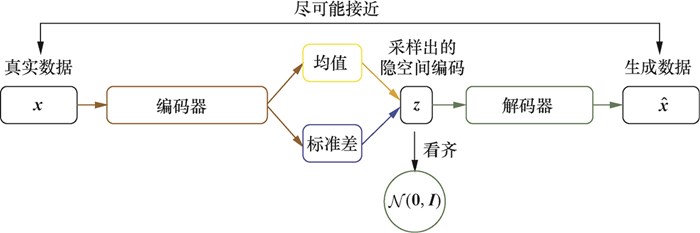
图5.2 变分自编码器(VAE)的基本框架
■生成式对抗网络(GAN)
GAN是专门为了优化生成任务而提出的模型。生成模型的一大难点在于如何度量生成分布与真实分布的相似度。一般情况下,我们只知道这两个分布的采样结果,很难知道具体的分布表达式,因此难以找到合适的度量方法。GAN的思路是,把这个度量任务交给一个神经网络来做,这个网络被称为判别器(Discriminator)。GAN在训练阶段用对抗训练方式来交替优化生成器
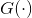
与判别器
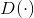
。整个模型的优化目标是
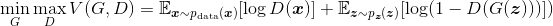
(5-1)
上述公式直观地解释了GAN的原理:判别器
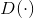
的目标是区分真实样本和生成样本,对应在目标函数上就是使式(5-1)的值尽可能大,也就是对真实样本
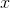
尽量输出1,对生成样本
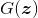
尽量输出0;生成器
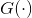
的目标是欺骗判别器,尽量生成“以假乱真”的样本来逃过判别器的“法眼”,对应在目标函数上就是让式(5-1)的值尽可能小,也就是让
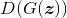
也尽量接近1。这是一个“MiniMax”游戏,在游戏过程中
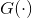
和
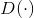
的目标是相反的,这就是GAN名字中“对抗”的含义。通过对抗训练方式,生成器与判别器交替优化,共同成长,最终修炼为两个势均力敌的强者。图5.3是GAN的基本框架图。

图5.3 GAN的基本框架
在了解了AE、VAE、GAN这3种模型的原理后,下面总结一下它们之间的联系和区别。
■AE和VAE的联系与区别
AE和VAE二者都属于有向图模型,模型的目的都是对隐变量空间进行建模;但AE只会模仿而不会创造,VAE则可以根据随机生成的隐向量来生成新的样本。
AE的优化目标是最小化真实样本与对应的生成样本之间的重构误差,但在VAE中,除了考虑重构误差之外,还加入了对隐变量空间的约束目标。
AE中编码器的输出代表真实样本对应的隐向量,而VAE中编码器的输出可以看作由两个部分组成:一部分是隐向量所对应的分布的均值;另一部分是标准差。计算均值的编码器就相当于AE中的编码器,而计算标准差的编码器相当于为重构过程增加噪声,使得解码器能够对噪声更为鲁棒(当噪声为0时,VAE模型就退化成AE)。
■GAN和AE/VAE的联系与区别
在VAE的损失函数中,重构损失的目的是降低真实样本和生成样本之间的差异,而迫使隐向量后验分布接近正态分布,实际上是增加了生成样本的不确定性,两种损失相互对立。这与GAN一样,它们内部都存在对抗思想,只不过VAE是将两部分同步优化的,而GAN则是交替优化的。
与AE相同的是,GAN的优化目标只涉及生成样本和真实样本之间的比较,没有VAE中对后验分布的约束。不同的是,GAN设计了判别器,并用对抗训练方式绕过了对分布间距离的度量,且在判断样本真假时不需要真实样本与生成样本一一对应(而在AE/VAE中都需要二者一一对应才能计算重构误差)。
GAN没有像AE那样从学习到的隐向量后验分布
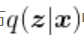
中获得生成样本
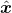
的能力,可能因此导致模式坍塌、训练不稳定等问题。另外,在AE/VAE中隐向量空间是数据的压缩编码所处的空间,隐向量用“精炼”的形式表达了输入数据的特征。如果我们想在抽象的语义层次上对数据进行操控,比如改变一张图像中人的发色,直接在原始数据空间中很难操作,而VAE在隐空间的表达学习能力,使得可以通过在隐变量空间上的插值或条件性嵌入等操作来实现对数据在语义层次上的操控。
问题2 原始GAN 在理论上存在哪些问题?
难度:★★★★★
分析与解答
在Goodfellow提出的原始GAN[1]中,模型的优化目标为式(5-1)。如果将判别器
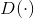
看作一个二分类器,对真实样本输出1,对生成样本输出0,
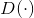
的优化目标可以解释为最大化该分类问题的对数似然函数,即最小化交叉熵损失。这个看起来简洁又直观的定义,在理论上存在一些问题。简单来说,就是在训练的早期阶段,目标函数式(5-1)无法为生成器提供足够大的梯度。这是因为,在一开始训练时,生成器还很差,生成的数据与真实数据相差甚远,判别器可以以高置信度将二者区分开来,这样
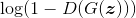
达到饱和,梯度消失。
上面只是做了简单描述,接下来我们给出更加理论的解释。当生成器

固定时,判别器的最优解
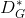
的公式为
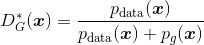
(5-2)
其中,
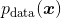
表示真实样本的概率分布,
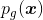
表示生成样本的概率分布(具体论证过程见参考文献[1])。当判别器达到最优时,生成器的损失函数为
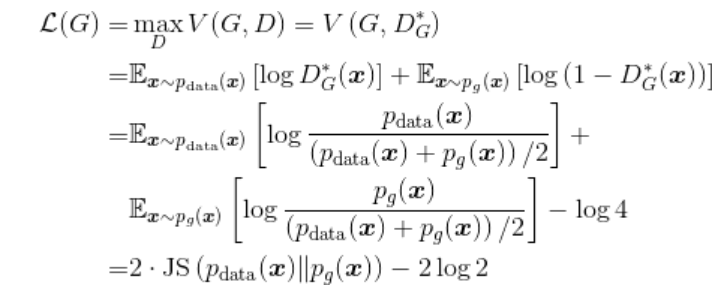
(5-3)
其中,JS(·)是JS散度(Jensen–Shannon divergence),它与KL散度类似,用于度量两个概率分布的相似度,其定义为
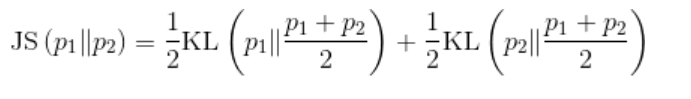
(5-4)
可以看到,JS散度的取值是非负的,当且仅当两个分布相等时取0,此时
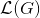
取得最小值
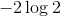
。
当判别器达到最优时,根据损失函数
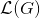
,此时生成器的目标其实是最小化真实分布与生成分布之间的JS散度。随着训练的进行,判别器会逐渐趋于最优,所以生成器也会逐渐近似于最小化JS散度。然而,JS散度有一个特性:当两个分布没有重叠的部分或几乎没有重叠时,JS散度为常数(这可以根据JS散度的定义式(5-4)得到)。那么在GAN中,真实分布和生成分布的重叠部分有多大呢?生成器一般是从一个低维空间(如128维)中采样一个向量并将其映射到一个高维空间中(比如一个
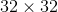
的图像就是1024维),所以生成数据只是高维空间中的一个低维流形(比如生成样本在上述1024维图像空间的所有可能性实际上是被128维的输入向量限定了)。同理,真实分布也是高维空间中的低维流形。高维空间中的两个低维流形,在这样“地广人稀”的空间中碰面的几率趋于0,所以生成分布与真实分布是几乎没有重叠部分的。因此,在最优判别器
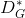
下,生成器的损失函数为常数,导致存在梯度消失问题。
为解决该问题,Goodfellow提出了改进方案,采用以下公式来替代生成器的损失函数:
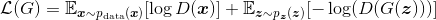
(5-5)
上述损失函数与原始版本有相同的纳什均衡点,但在训练早期阶段可以为生成器提供更大的梯度(见参考文献[1])。然而,改进后的损失函数也存在不合理之处。将式(5-5)进行变换,有
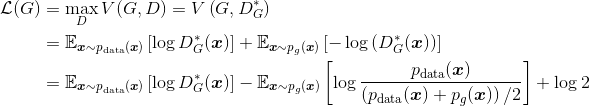
(5-6)
式(5-6)中第一项不依赖生成器,最小化损失函数相当于最小化
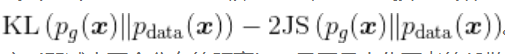
。这就既要最小化生成分布与真实分布的KL散度(即减小两个分布的距离),又要最大化两者的JS散度(即增大两个分布的距离),这会在训练时造成梯度的不稳定。另外,KL散度是一个非对称度量,因此还存在对不同错误惩罚不一致的问题。举例来说,当生成器缺乏多样性时,即当
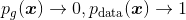
时,
对损失函数贡献趋近于0;而当生成器生成了不真实的样本时,即当
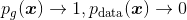
时,惩罚会趋于无穷大。真实数据的分布往往是高度复杂并且多模态的,数据分布有很多模式,相似的样本属于一个模式。由于惩罚的不一致,生成器宁愿多生成一些真实却属于同一个模式的样本,也不愿意冒着巨大惩罚的风险去生成其他不同模式的具有多样性的样本来欺骗判别器,这就是所谓的模式坍塌。
总的来说,原始GAN在理论上主要有以下问题。
(1)原始GAN在判别器
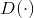
趋于最优时,会面临梯度消失的问题。
(2)采用
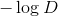
技巧改进版本的生成器同样会存在一些问题,包括训练梯度不稳定、惩罚不平衡导致的模式坍塌(缺乏多样性)、不好判断收敛性以及难以评价生成数据的质量和多样性等。
本文摘自《百面深度学习 算法工程师带你去面试》

本书仍然采用知识点问答的形式来组织内容,每个问题都给出了难度级和相关知识点,以督促读者进行自我检查和主动思考。书中每个章节精心筛选了对应领域的不同方面、不同层次上的问题,相互搭配,展示深度学习的“百面”精彩,让不同读者都能找到合适的内容。
本书适合相关专业的在校学生检查和加强对所学知识点的掌握程度,求职者快速复习和补充相关的深度学习知识,以及算法工程师作为工具书随时参阅。此外,非相关专业但对人工智能或深度学习感兴趣的研究人员,也可以通过本书大致了解一些热门的人工智能应用、深度学习模型背后的核心算法及其思想。
生成式对抗网络书籍推荐《PyTorch生成对抗网络编程》

本书以直白、简短的方式向读者介绍了生成对抗网络,并且教读者如何使用PyTorch按部就班地编写生成对抗网络。全书共3章和5个附录,分别介绍了PyTorch基础知识,用PyTorch开发神经网络,改良神经网络以提升效果,引入CUDA和GPU以加速GAN训练,以及生成高质量图像的卷积GAN、条件式GAN等话题。附录部分介绍了在很多机器学习相关教程中被忽略的主题,包括计算平衡GAN的理想损失值、概率分布和采样,以及卷积如何工作,还简单解释了为什么梯度下降不适用于对抗式机器学习。