目录
一、定点数表示
在计算机系统的发展过程中,曾经提出过多种方法表达实数。典型的比如相对于浮点数的定点数(Fixed Point Number)。
在这种表达方式中,小数点的位置固定不变,一般用来表示一个纯小数或者整数。
数的定点表示熟知的取值范围有限,表示一个纯小数时,小数点固定在符号位之后;表示一个整数时,小数点固定在数据最后一位之后。
货币的表达就可以使用这种方式,比如 88.00 或者 00.88 可以用于表达具有四位精度,小数点后有两位的货币值。由于小数点位置固定,所以可以直接用四位数值来表达相应的数值。
二、浮点数表示
定点数表达法的缺点在于其形式过于僵硬,固定的小数点位置决定了固定位数的整数部分和小数部分,不利于同时表达特别大的数或者特别小的数。
所以使用浮点数表示的原因:
定点数的表示范围小,为了能表示两个大小相差很大的数据,需要很长的机器字长,导致数据存储单元的利用率往往很低
最终,绝大多数现代的计算机系统采纳了所谓的浮点数表达方式。
这种表达方式利用科学计数法来表达实数,即用一个
尾数,一个
基数,一个
阶数以及一个
符号位来表达实数。
比如 123.45 用十进制科学计数法可以表达为 (-1)^0 x 1.2345 × 10^2 ,其中 (-1)^0的0表示符号位(备注:如果表示负数,符号位为1),1.2345 为尾数,10 为基数,2 为阶数。浮点数利用指数达到了浮动小数点的效果,从而可以灵活地表达更大范围的实数。
1、计算机中的浮点数表示

计算机中
r
取
2
、
4
、
8
、
16
等,
S 小数、可正可负,
j 整数、可正可负

- Sf 代表浮点数的符号
- n 其位数反映浮点数的精度
- m 其位数反映浮点数的表示范围
- jf 和 m 共同表示小数点的实际位置
浮点数的表示范围
这个计算公式看起来比较复杂,其实就是计算特定数取得最大时的数据范围,仔细分析就可以得出来了,没啥好纠结的。

问题:设机器数字长为 24 位,欲表示± 3 万的十进制数, 试问在保证数的最大精度的前提下,除阶符、数符各 取 1 位外,阶码、尾数各取几位?

分析:
- 尾数反应了浮点数的最大精度,所以我们尽可能使尾数n的位数最大。
- 因为 2^14 < 3000 < 2^15;所以为表示±3万的十进制数,阶数m >=15 ;
- 15使用二进制表示为1111;所以机器字长最少占用4位,机器数字长总共为 24 位,除去两个符号位,因此尾数n的位数最大为18位。
2、浮点数的规格化
为什么要进行浮点数的规格化?
对浮点数进行规格化的主要目的是尽可能的保证数据的精度。
如果不进行规格化,尾数的小数点后边可能会有若干个0,0占据了尾数表示有效数据(不为0的数据)的字长,导致可以表示有效数据的字长变短,降低数据的精度。
因此,我们对浮点数进行规格化,就要使尾数中表示有效数据的位置尽可能的多。
浮点数的规格化形式
比如
- r = 2 尾数最高位为 1
- r = 4 尾数最高 2 位不全为 0 ——> 2位二进制数表示一位4进制数
- r = 8 尾数最高 3 位不全为 0 ——> 3位二进制数表示一位8进制数
- ...
因此,基数不同,浮点数的规格化形式不同,规格化形式不同,基数 r 越大,浮点数的精度降低
如何对浮点数进行规格化?
对浮点数进行规格化实际上就是把尾数部分多余的0移除掉,通过操作阶数来保证原来的数值(真值)不变,这种方式称为做规。
问题一:
将写成二进制定点数、浮点数及在定点机和浮点机中的机器数形式。其中数值部分均取 10 位,数符取 1 位,浮点数阶码取 5 位(含1位阶符),尾数规格化
解:
设
x =
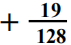
二进制形式: x
= 0.0010011 ——> 10011(19) / 2^7(128) ——>小数点向左移7位
定点表示: x
= 0.0010011
000
——>
数值部分均取 10 位,所以扩展3位0
浮点规格化形式 :
 ——> -10(2)为二进制码,表示向右移动两位小数点
——> -10(2)为二进制码,表示向右移动两位小数点

问题二:将 –58 表示成二进制定点数和浮点数, 并写出它在定点机和浮点机中的三种机器数及阶码为移码、尾数为补码的形式(其他要求同问题一)。

机器零
- 当浮点数 尾数为 0 时,不论其阶码为何值按机器零处理
- 当浮点数 阶码等于或小于它所表示的最小数 时,不论尾数为何值,按机器零处理