题目
BUPT 2018 计算机 ProblemC
一个大于等于2的整数,如果可以分解为8个或8个以上的素数相乘,则称其为发财数,让你输出第n个发财数
输入描述
输入一个整数t,代表有t组数据(t<1000)
输入一个正整数n,(n<=10000)
输出描述
输出第n个发财数。
示例
输入
1
1
输出
256
题解
王道机试指南上有关于素数筛法和分解素因数的相关讲解,当年看过那部分的人肯定就有思路,没看过的基本凉凉
#include<bits/stdc++.h>
#define MAX 350001//最小遍历到35w,就能找到第1w多个发财数
using namespace std;
int isCom[MAX]= {
0}; //合数标记,为1代表是合数
vector<int>prime;//记录素数集合
/*分解质因数,找发财数*/
int cal(int n)
{
int count=0;//发财数个数
for(int i=2; i<MAX; i++)
{
if(isCom[i]==1)//合数
{
int pcount=0;//素因子个数
int j=0;
int tmp=i;
int bound=sqrt(i);//sqrt函数相当耗时,放在while里会超时
while(j<prime.size()&&prime[j]<bound)
{
if(tmp%prime[j]==0)
{
tmp/=prime[j];
pcount++;//i增加一个素因子
if(pcount==8)
{
if(++count==n)
return i;
}
}
else
j++;
}
//最后剩下的是素数且是发财数
if(tmp!=1&&++pcount==8)
{
if(++count==n)
return i;
}
}
}
return -1;
}
/*欧拉线性筛法*/
void find_prime()
{
for(int i=2; i<MAX; i++)
{
//是素数,加入素数集合
if(isCom[i]==0)
prime.push_back(i);
//把"i*最小素数"标记为合数
for(int j=0; i*prime[j]<MAX&&j<prime.size(); j++)
{
isCom[i*prime[j]]=1;
//找到最小素因子退出
if(i%prime[j]==0)
break;
}
}
}
int main()
{
find_prime();
int t;
cin>>t;
while(t--)
{
int n;
cin>>n;
//找第n个发财数
cout<<cal(n)<<endl;
}
}
当时有一个临界条件写错了,后来又代码超时,折磨了我好几天…
小结
素数筛法
主要分为这三类
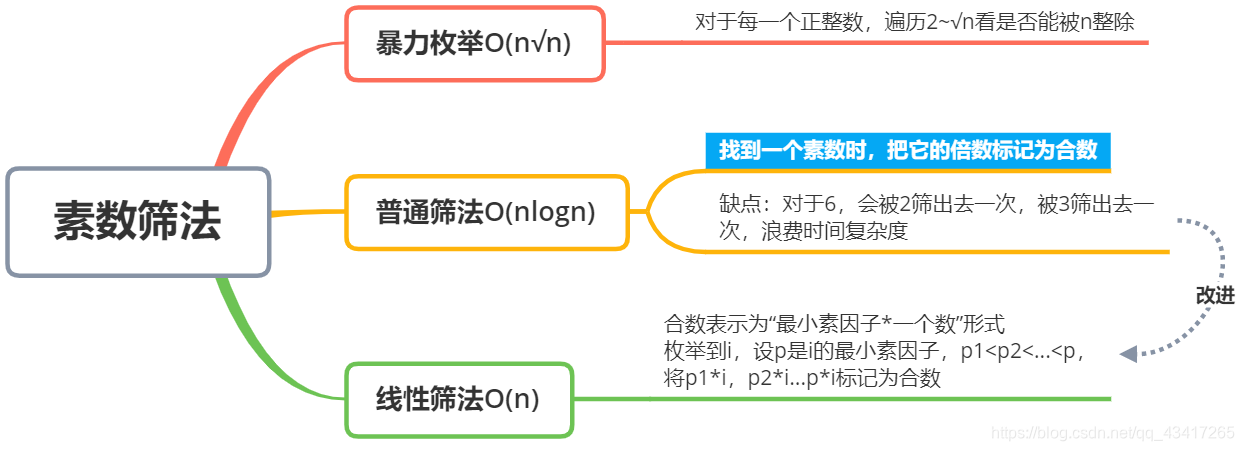
暴力枚举
/*暴力枚举素数*/
void find_prime()
{
for(int i=2;i<MAX;i++)
{
int bound=sqrt(i);
int flag=1;//素数标志
for(int j=2;j<=bound;j++)
{
//有可被整除的数则i为合数
if(i%j==0)
{
flag=0;
break;
}
}
if(flag)
cout<<i<<"是素数"<<endl;
else
cout<<i<<"是合数"<<endl;
}
}
普通筛法
/*普通素数筛法*/
void find_prime()
{
for(int i=2; i<MAX; i++)
{
//是素数,把倍数标记为合数
if(isCom[i]==0)
{
prime.push_back(i);//加入素数集合
for(int k=2; i*k<MAX; k++)
isCom[i*k]=1;//倍数为合数
}
}
}
线性筛法
/*欧拉线性筛法*/
void find_prime()
{
for(int i=2; i<MAX; i++)
{
//是素数,加入素数集合
if(isCom[i]==0)
prime.push_back(i);
//把"i*最小素因子之前的素数"标记为合数
for(int j=0;i*prime[j]<MAX&&j<prime.size();j++)
{
isCom[i*prime[j]]=1;
//找到最小素因子退出
if(i%prime[j]==0)
break;
}
}
}
参考视频:基础数论
分解质因数
前提是在素数筛法筛出所有素数之后
/*分解质因数*/
void cal(int n)
{
for(int i=2; i<n; i++)
{
if(isCom[i]==1)//合数
{
cout<<i<<"可分解为:";
int j=0;
int tmp=i;
int bound=sqrt(i);//sqrt函数相当耗时,放在while里会超时
while(j<prime.size()&&prime[j]<=bound)
{
if(tmp%prime[j]==0)
{
tmp/=prime[j];
cout<<prime[j]<<" ";
}
else
j++;
}
//最后剩下的是素数
if(tmp!=1)
cout<<tmp;
cout<<endl;
}
}
}
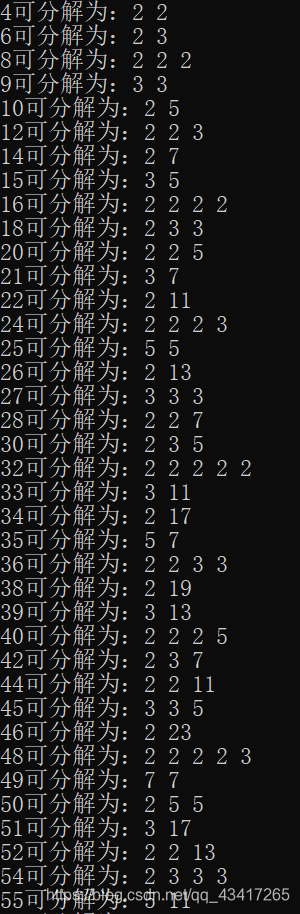
运行结果: