余弦相似度:
在我们计算相似度时,常常用到余弦夹角来判断两个向量或者矩阵之间的相似度,Cosine(余弦相似度)取值范围[-1,1],当两个向量的方向重合时夹角余弦取最大值1,当两个向量的方向完全相反夹角余弦取最小值-1,两个方向正交时夹角余弦取值为0。
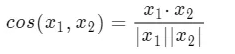
x 1 x_1 x1 和 x 2 x_2 x2 分别是输入的两个向量。
基于python的代码:
import numpy as np
x_1 = np.array([1,3,6,2,3,6])
x_2 = np.array([3,4,1,5,7,8])
def cos_sim(a, b):
a_norm = np.linalg.norm(a)
b_norm = np.linalg.norm(b)
cos = np.dot(a,b)/(a_norm * b_norm)
return cos
print(cos_sim(x_1,x_2))
基于sklearn的python代码:
import numpy as np
from sklearn.metrics.pairwise import cosine_similarity
x_1 = np.array([1,3,6,2,3,6]).reshape(1,6)
x_2 = np.array([3,4,1,5,7,8]).reshape(1,6)
con_sim = cosine_similarity(x_1,x_2) #输入必须是一个二维的,如果是一个矩阵的话,输入的是矩阵的每行的
print(con_sim)
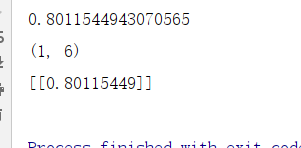
可以看出两者计算出的相似度是一样的。