1. 栈 stack

栈是限制在一端进行插入操作和删除操作的线性表（俗称堆栈），允许进行操作的一端称为“栈顶”，另一固定端称为“栈底”，当栈中没有元素时称为“空栈”。向一个栈内插入元素称为是进栈（push）；
从一个栈删除元素称为是出栈（pop）

特点：后进先出（Last In First Out / LIFO）

1.1 栈的方法

push：将数据入栈；

pop：删除并返回栈顶元素（此方法会修改栈）

peek：返回栈顶元素，但不修改栈

size：查看栈内的数据个数

isEmpty：判断栈内是否为空

isString：将栈内的数据转化为字符串输出

clear：清空栈

1.2 栈的封装

class Stack(object):
    def __init__(self):
        self.stack = []
    def push(self, value): # 入栈
        self.stack.append(value)
        print(f"入栈元素为{value}")
    def pop(self): # 出栈
        if self.is_empty():
            raise  Exception("栈为空")
        item = self.stack.pop()
        print(f"出栈元素为{item}")
        return  item
    def is_empty(self): # 判断栈是否为空
        return  len(self.stack) == 0
    def top(self): # 返回栈顶元素
        if self.is_empty():
            raise  Exception("栈为空")
        return  self.stack[-1]
    def __len__(self):
        return  len(self.stack)
if __name__ == '__main__':
    stack = Stack()
    stack.push(1)
    stack.push(2)
    stack.push(3)
    print(f'长度为：{len(stack)}')
    stack.pop()
    print(stack.is_empty())
    print(f'栈顶元素：{stack.top()}')

执行结果：
入栈元素为1
入栈元素为2
入栈元素为3
长度为：3
出栈元素为3
False
栈顶元素：2

2. 队列 queue

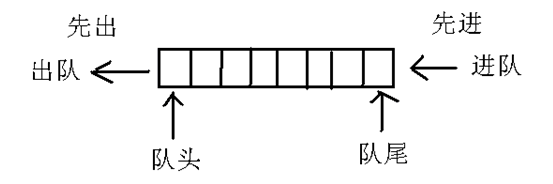
队列是限制在一端进行插入操作和另一端删除操作的线性表，允许进行插入操作的一端称为“队尾”，允许进行删除操作的一端称为“队头”，，当队列中没有元素时称为“空队”。

特点：先进先出（FIFO）

在这里插入图片描述

队列的封装

class Queue(object):
    def __init__(self):
        self.queue = []
    def enqueue(self,value): #入队列
        self.queue.insert(0,value)
        print(f"入队列元素为{value}")
    def dequeue(self): #出队列
        if self.is_empty():
            raise Exception("队列为空")
        item=self.queue.pop()
        print(f'出队列元素为{item}')
    def is_empty(self): # 判断空
        return len(self.queue)==0
    def __len__(self): #长度
        return len(self.queue)
    def first(self): #队首
        if self.is_empty():
            raise Exception("队列为空")
        return self.queue[-1]
    def last(self): #队尾
        if self.is_empty():
            raise Exception("队列为空")
        return self.queue[0]
if __name__ == '__main__':
    queue = Queue()
    queue.enqueue(1)
    queue.enqueue(2)
    queue.enqueue(3)
    print(f'长度：{len(queue)}')
    queue.dequeue()
    print(queue.is_empty())
    print(f'队头：{queue.first()}')
    print(f'队尾：{queue.last()}')

执行结果：
入队列元素为1
入队列元素为2
入队列元素为3
长度：3
出队列元素为1
False
队头：2
队尾：3

3. 二叉树 binaryTree

3.1 简介

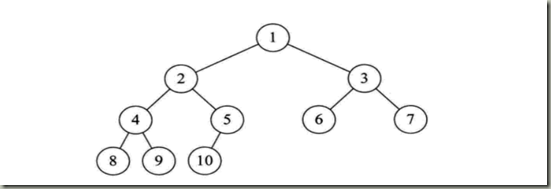
二叉树是树的特殊一种，具有如下特点：

每个结点最多有两颗子树，结点的度最大为2。
左子树和右子树是有顺序的，次序不能颠倒。
即使某结点只有一个子树，也要区分左右子树

3.2 一般二叉树的性质

1、在非空二叉树的i层上，至多有2i-1个节点(i>=1)。通过归纳法论证。

2、在深度为K的二叉树上最多有2k-1个结点（k>=1)。通过归纳法论证。

3、对于任何一棵非空的二叉树,如果叶节点个数为n0，度数为2的节点个数为n2，则有: n0 = n2 + 1

在一棵二叉树中，除了叶子结点（度为0）之外，就剩下度为2(n2)和1(n1)的结点了。则树的结点总数为T = n0+n1+n2;在二叉树中结点总数为T，而连线数为T-1，所以有：n0+n1+n2-1 = 2*n2 +n1;最后得到n0 = n2+1;

3.3 二叉树的封装