相似度算法--莱文斯坦距离加入同义词逻辑

一、背景

在问题检索中，依赖文本相似度给用户做推荐问题，假设1.0分为满分，那么：

1.0分表示完全匹配：可以将问题准确推送给用户

0.8分表示高度相似：可以将问题推荐给用户

0.6分表示低度相似：......

根据这样的规则对用户的检索做出回应。其实Lucene基于TF-IDF改造的相关度排序算法也有分值，但是和业务所需要的相似度不贴合，所以其得分只作为第一步结果筛选依据。关于Lucene打分公式可以看看这篇文章，Lucene的源码也做过详细解析，Lucene检索源码解析（上）和Lucene检索源码解析（下），感兴趣的朋友可以研究一下。

二、莱文斯坦距离

文本相似度算法有很多，我这里选择的是编辑距离算法-莱文斯坦距离(Levenshtein)。它表示的是将一个字符串a变换为另一个字符串b，所需要的字符插入、删除、替换的次数。

对于字符串a和b，分别用|a|和|b|代表其长度，那么他们的莱文斯坦距离表示为： $\large lev_{a,b}(|a|,|b|)$ ，它符合：

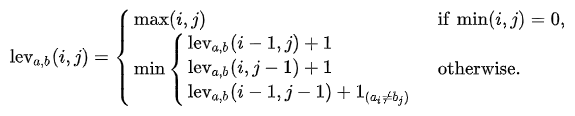
它表示，若a或b有一个是空串，那么距离为非空串的长度（max运算）；否则，进入min运算，三个公式从上到下分别表示，从a中删除一个字符、往a中添加一个字符、字符替换。

第三个公式中的 $\large I_{(a_i\neq b_j)}$ ，是一个指示函数，它表示当 $\large a_i \neq b_j$ 时为1，反之等于0。意思就是如果字符相同，则不用替换，如果字符不同，则需要1次替换。

比如将“kitten”一字转成“sitting”的莱文斯坦距离为3（例子来自维基）：

kitten → sitten （k→s）
sitten → sittin （e→i）
sittin → sitting （插入g）

关于莱文斯坦距离的详细内容，可以看看维基定义，这里就不赘述了。

三、相似度计算

结合业务之后，计算距离就不再是字符变更，而是词。对于两个文本，要先对内容做分词，去除停顿词等操作。分词是词法分析中最基本的任务，它把一个语句拆分为多个词，特征提取一般也要建立在分词的基础上。其可以基于词典、基于统计或者基于规则等，算法也比较多，比如最大匹配、隐马尔科夫模型等，不过分词不是本章节的重点。

在分词之后，莱文斯坦距离的计算目标就变成了：将一个词列表变换为另一个词列表，所需要的词删除、添加、替换的次数（操作从字符变成了词）。但是这里要注意的是分词结果的顺序问题，在一些情况下，词的顺序是在一定程度上代表了语义的，比如：

分词1：我吃饭后回家

分词2：我回家后吃饭

字符串本身是一个整体，按照字符拼接顺序处理即可，但是分词结果本身是一个词的列表，所以要注意这个问题。

结合分词之后，加入同义词的逻辑就是：判断需要一次替换操作的条件为：!item1.equals(items2) && 不是同义词(item1,item2)，即指示函数变更为： $\large I_{(a_i\neq b_j \&\& isNotSynonym(a_i,b_j)) }$ 。

得到距离之后，按照要求做一个归一化处理即可，所以我们需要考虑的问题就是如何归一化处理和在兼容内存消耗下较高效率的判断两个词是否为同义词。

四、同义词判定

出于对存储和读取效率的考虑，主要就是找到一个适合的数据结构实现字典功能，主要实现有：有序列表(查询时使用二分法查找)、二叉排序树、跳表、HashMap、FST等，出于多方面因素考虑，项目中使用的lucene中也有开源的FST实现，FST对于内存压缩优势较大，而查询效率也较高，所以选择使用FST作为字典实现比对同义词。

注：FST，即Finite State Transducer，有穷状态转换器，其通过单词前后缀的重复利用，最终生成一个无环图，在很大的程度上减少了内存消耗。FST表示为字典结构:FST<key,value>时，只需要O(lengthOf(key))的时间复杂度。关于FST的细节，可自行查阅。

在当前实现中，我们已经根据同义词库创建好了FST，每个都词有一个hash id，在初始化同义词库时，对于一个词，使用几个字节存储其同义词的数量，然后将它们的hash id按照规则存储在一起，方便读取。这样对于一个输入词，我们能快速获取到其同义词的hash id列表(多个同义词)，然后根据目标词的hash id进行比对即可。查询同义词hash id列表的相关代码片段如下：

ByteArrayDataInput reader = new ByteArrayDataInput(bytesRef.bytes, bytesRef.offset, bytesRef.length);
//获取长度，如果多个字节存储了长度，在readVInt的时候自动递增position
int size = reader.readVInt();
size >>= 1;
if (logger.isDebugEnabled()) {
    logger.debug("[FST跟踪]text:{},同义词数量:{}", text, size);
}

//获取所有同义词的hash id
int[] results = new int[size];
int index = 0;
while (!reader.eof()) {
    results[index++] = reader.readVInt();
}
return results;

注：同义词库记录了同义词关系，可以是文件或者数据表等等，其表征了哪些词互为同义词。比如在文件中，将属于同义词的词列在同一排：

晚上黑夜夜间

吃饭进食干饭

在指示函数的实现中，根据hash id进行比对就可以了：

private boolean isSynonyms(int[] outputs, int hash) {
        //如果同义词较多的话，可以优化匹配方式，这里演示就直接遍历,O(n)
        if (outputs != null && hash > 0) {
            for (int output : outputs) {
                if (output == hash) {
                    return true;
                }
            }
        }
        return false;
    }

五、归一化算法

编辑距离的结果是距离，表征为一个数值，但是我们需要的是一个分值score(0.0<=score<=1.0)来表征相似度，所以需要做归一化处理。这里首先考虑使用线性函数进行归一化处理，标准的线性归一化处理公式为： $x_{norm}=\frac{x-x_{min}}{x_{max}-x_{min}}$ 。将原始数据进行等比例缩放。

在此处的距离中，简化处理为： $x=\frac{cost}{maxSize(word)}$ 。其中cost为消耗步数，maxSize(word)为最长词列表长度。对于两个语句，变换距离(cost)越大，就代表越不相似，所以最终得分公式为： $score=1-\frac{cost}{maxSize(word)}$ 。

现在需要考虑另外一个问题，编辑距离是一个量化的结果，其本身表征的意义和我们的直观感受结果可能有所不同，特别是在极端情况下。比如以下两个语句：

语句：回家吃饭分词结果：回家吃饭

语句：回家种花分词结果：回家种花

根据编辑距离算法，他们的相似度得分为0.5分，从理性上讲，他们有一半的词是相同的，那么0.5分可以理解。工程化后，从感性上讲，如果语句很长（分词列表很长），0.5分的相似度似乎并不足以我们推荐给用户。但是对于上面这种情况，虽然是0.5分，但是由于语句本身很短，也是值得我们推荐给用户的。也就需要对这种情况特殊处理(提高其分值)，但是不能影响其它情况，所以需要设计贴合业务的归一化算法。由于新算法业务强相关，这里就不贴出来了。

六、实现

    @Override
    public double similarScore(List<String> words1, List<String> words2, Long companyId) throws Exception {
        if (words1 == null || words2 == null) {
            return 0.0D;
        }

        double costs;
        double maxLength;
        //首先判断极端情况的距离
        if (words1 == null) {
            costs = words2.size();
            maxLength = costs;
        } else if (words2 == null) {
            costs = words1.size();
            maxLength = costs;
        } else {
            //都不为空
            String[] s_segs = words1.toArray(new String[]{});
            words1.clear();

            String[] t_segs = words2.toArray(new String[]{});
            words2.clear();

            maxLength = Math.max(s_segs.length, t_segs.length);
            //使用两个一维数组迭代实现
            if (s_segs.length < t_segs.length) {
                // 为了节约内存，将元素较少的列表当做目标列表
                String[] tmp = s_segs;
                s_segs = t_segs;
                t_segs = tmp;
            }
            int s_length = s_segs.length;
            int t_length = t_segs.length;

            int pre[] = new int[t_length + 1]; //保存前一行记录
            int current[] = new int[t_length + 1]; //当前行记录
            int[] tmp;//用以交换pre和current
            //初始化第一行
            for (int i = 0; i < pre.length; i++) {
                pre[i] = i;
            }
            //迭代计算
            String s_w;
            String t_w;
            int cost;
            for (int i = 1; i <= s_length; i++) {
                //第一列的值设置为j
                current[0] = i;
                s_w = s_segs[i - 1];
                //计算一行的值
                for (int j = 1; j <= t_length; j++) {
                    t_w = t_segs[j - 1];
                    //指示函数的实现
                    if (s_w.equals(t_w) || isMutualSynonyms(companyId, s_w, t_w)) {
                        cost = 0;
                    } else {
                        cost = 1;
                    }
                    //从新增、删除、替换中选取最小值
                    current[j] = Math.min(Math.min(current[j - 1] + 1, pre[j] + 1), pre[j - 1] + cost);
                }
                //将当前行设置为前一行的值，为下次做准备
                tmp = pre;
                pre = current;
                current = tmp;
            }
            costs = pre[t_length];
        }
        return normalization(costs, maxLength);
    }

    private double normalization(double costs, double max) {
        return 1 - (costs / max);
    }