一、单向链表
上一篇文章我们提到了,和数组一样,链表也属于线性表结构,但是链表是链式的,而数组是顺序的。它和数组最大的区别就是,它的元素存储并不依赖连续的内存空间,元素之间使用指针来实现逻辑顺序。
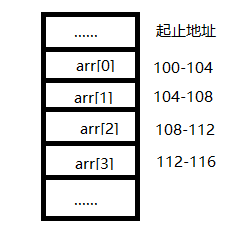
如果创建一个长度为4的数组,其内存布局可能是下图这样,它要求元素的内存空间必须连续以实现常量阶的寻址操作,但是如果内存中没有这么大的整块儿空间,那么内存分配会失败。
而如果是链表结构的话,每个元素的内存地址可以任意分布,元素和元素之间使用指针:前一个元素保存一个指向后一个元素内存地址的指针(单向链表)。指针就像一根线连接两个元素。其内存布局可能是下图这样:
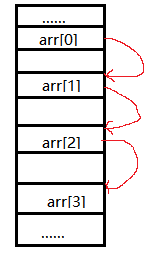
看的出来,首先从内存分配上,同样是4个元素,如果内存中有足够的、“分散”的空闲内存,我们虽然无法使用数组,但是链表能够满足我们的存储要求。但是我们同样发现,链表里的每个元素不能像数组那么“纯粹”了。因为每个元素必须要有一个指向下一个元素内存地址的指针。基于这种结构,我们在初始化一个链表的时候也不用像数组那样指明需要存储多少个元素了,只需要一个节点一个节点的分配,只要内存足够,就可以一直扩展,所以我们也称链表为一种动态集合。
我们都知道,链表的删除和插入效率是很高(O(1),这里针对的只是具体的删除/插入操作本身,后面会解释)的,只需要改变指针的指向即可,不需要像数组那样移动元素(当然对于不同的场景,也不一定非要移动元素)。
在c语言中,我们在进行链表操作的时候,有一些需要注意的点,不然容易发生内存泄漏。比如有如下单向不循环链表:A->B->C。我们要删除B节点,可以直接令 A.next=C.address,虽然B节点是被“删除”了,但是节点的内存并没有被释放,并且你找不到这块儿内存地址了。当然,在有内存自动回收的语言(比如JAVA)中,我们都不用怎么去理会这点,但还是得明白其中的缘由。具体到我们的实际场景中,对于一个链表的删除操作,一般就两个情况:
1、删除链表中,节点值等于某指定值的节点
2、删除链表中,某指定指针指向的节点
首先第一种情况,无论如何我们都要去寻找到对应的节点,所以时间复杂度为O(n),虽然找到之后的删除操作是O(1),但是整个时间复杂度还是为O(n);
对于第二种情况,我们要考虑到,即使给定了要删除的节点,但是删除操作需要知道该节点的前一个节点,因为要修改指向关系。对于单向链表而言,我们还是要重头遍历,找到被删除节点的前一个节点,然后才能进行删除操作,所以时间复杂度也是O(n);下面提到的双向链表,由于可以根据指定节点找到它的前驱节点,所以时间复杂度就为O(1)。
这点一定要注意,如果直接说在给定单向链表中删除一个节点的时间复杂度为O(1),其实是不严谨的。
链表操作其实很简单,只需要把节点指针的概念理清楚就可以了,不能靠“记忆”来学习链表。比如我在面试的时候都会抛出一个问题:如下链表:A->B,现在要在A节点之后插入C节点,很多人的回答都是,先令A指向C(A.next=C.address),再令C指向B(C.next=B.address)。可是A先指向了C,那B的地址还怎么找到呢?所以应该是先让C.next=A.next.address,然后A.next=C.addres。
接下来我们来思考一个问题:现在有一个单向不循环的链表,只知道头结点head,需要我们找到倒数第N个节点,该怎么找呢?
要解决这个问题很简单,我们马上就能想到一种方法:我们先遍历一遍,找到链表的长度,然后根据长度和N,算出正向第几个,再遍历一次即可,时间复杂度为O(n)。但我们还可以换一种思路:用两个指针配合使用。具体怎么操作呢?
我们现在不考虑极端情况,认为链表长度大于等于N,首先令A和B两个指针都指向头结点,然后A指针不动,B指针向后移动N个节点,然后A和B指针同时向后移动,直到B指针为空,这个时候A指针所在的位置就是倒数第N个位置了。解释一下:我们设总节点数为M(M>=N),那么倒数第N个即正数第M-N+1个,我们先让B指针移动N个节点,A才开始移动,当B指针到达尾节点时,A指针所在的位置就是第M-N个,这时候再往后移动一个位置,B指针即为空,A就到倒数第N个节点的位置了。(描述中说的第几个,是从1开始的哈)
看的出来,这要比第一种方式少一次循环,虽然它们的时间复杂度都是O(n)。这进一步说明了,时间复杂度只是在总体上对一个算法进行评估,其结果并不精确。另外,我们多用了一个节点指针来跟随头结点移动,这就是一种空间换时间的思想,虽然空间复杂度为O(1)。我们不能单纯的说一个算法好或者不好,适合具体应用场景的才是最好的,另外,我们追求的也并不是单方面的时间或者空间,需要根据实际情况来做平衡取舍,比如空间比较充足,对时间要求较高时,可以适当牺牲点儿空间,反之亦然。
注:这种使用两个指针来错位移动的思想在很多地方都有运用,比如我们可以通过快慢指针寻找链表的中间位置:两个指针A和B都指向头节点,A移动一个节点,B则移动两个节点。当B移动到末尾时,比如B移动了N个节点到达末尾,那么A则移动了N/2个节点(当然这里只是简单的说法,我们还需要做一些特殊情况的处理,比如链表长度为1,比如我们是怎么定义第N个的等等)。
二、双向链表
双向链表就是在单项链表的基础上增加了一个前驱指针,用于保存前一个元素的地址。所以双向链表中的每个节点都至少需要两个属性:前驱指针(prev)和后继指针(next)。而头节点的前驱为空,即:head.prev=NIL,尾节点的后继为空,即:tail.next=NIL。

接下来我们以双向链表来举例实现搜索、插入、删除等操作。当然,在这之前我们需要先定义一些东西:链表中的每个节点包含三个属性,一个前驱节点(prev),一个后继节点(next),一个节点本身的值(value)。
1、搜索
给定头结点(head),我们要查找链表中节点值(value)为指定值(baseValue)的节点,这里和单项链表的操作是一样的。定义如下:doSearch(head,baseValue):
doSearch(head,baseValue):
while head != NIL and head.value != baseValue
head = head.next
return head
2、插入
给定头结点,我们在链表中节点值(value)为指定值(baseValue)的节点之后插入一个指定节点m,如果找不到节点则插入到表头位置,定义如下:doInsert(head,baseValue,m):
doInsert(head, baseValue, m):
x = doSearch(head, baseValue)
if x != NIL
m.next = x.next
if x.next != NIL
x.next.prev = m
m.prev = x
x.next = m
else
m.next = head
if head != NIL
head.pre = m
m.pre = NIL
head = m3、删除
我们这里就不删除指定值的节点了,直接提供一个m节点,从链表中删除该节点,定义如下:doDelete(head,m):
doDelete(head, m):
if m.prev != NIL
m.prev.next = m.next
else
head = m.next
if m.next != NIL
m.next.prev = m.prev
free(m)三、循环链表
顾名思义,循环链表就是在链表的基础上首尾相连,整个链表形成一个环状。如果是单向循环链表,则:tail.next=head;如果是双向循环链表,则:head.prev=tail,tail.next=head。比如双向循环链表看起来像是下面这样:

四、哨兵
哨兵本身其实是一个“哑”对象,它可以用来简化边界条件的处理。以我们上面的双向链表删除操作为例子。我们需要针对要删除节点所在位置是在链表头还是链表尾做特殊处理。如果元素不是表头也不是表尾,则删除操作其实可以很简单:
doDelete(T, m):
m.prev.next = m.next
m.next.prev = m.prev
free(m)所以,我们可以对原链表做一个处理:在链表中添加一个节点:T,该节点和链表中的其它节点有相同的属性,但是为空,然后将该节点置于原链表的表头和表尾之间,即:T.next=head,T.prev=tail。这样我们就把原双向链表转换成了一个双向循环链表,此链表永远不会为空,因为至少有一个T节点,我们也不用再对操作节点是表头或是表尾进行特殊处理了,这个T节点就称作为“哨兵”,而这种带哨兵的链表可以叫做“带头链表”,头指针(head)指向哨兵节点(T)。所以带头链表看起来可能是这样子的:
原链表为空:

原链表不为空:

接下来我们看哨兵能给我们带来什么便利。
首先,我们加入哨兵对doSearch操作可没有什么好处,和之前一样,还是要去挨着寻找;然后是删除操作,我们上面已经提到了,由于不需要考虑头尾节点,所以只需要简单的3行代码就可以实现节点的移除;再看插入操纵,我们假设已经找到了需要插入的位置:x,那么插入节点m的操作成了:
doInsert(T, x, m):
m.next = x.next
m.prev = x
x.next = m
x.next.prev = m从另一个方面说,哨兵其实只是一个概念上的东西,并不是单独指链表中的“哑”节点。它的目的是简化边缘处理,在很多地方我们都可以使用它,比如一些排序算法、动态规划等等。这样说起来比较抽象,下面举个简单的例子进行说明。为了区别上面的例子,现在我们以数组举例:给定一个数组array和一个元素m,找到m在array中的下标位置,如果不存在则返回-1(array中最多存在一个m)。我们的实现可能是这样的:
doSearch(array, m):
index = 0
while index < array.length
if array[index] == m
return index
index++
return -1上面的实现中,while的每一次循环都会有两次判断,一次++,现在我们用哨兵的思想改造一下:首先看m是否位于array的末尾,如果在末尾,就立即返回array.length-1;否则拿一个变量保存array的末尾元素,然后将m元素放到array的末尾,开始while循环:下标一直往后移直到找到m元素。这里和之前不一样,现在我们明确知道最后一个元素就是m,所以可以忽略length的判断,以找到元素m作为结束循环的条件,最后我们把原本的末尾元素恢复到数组中。如下所示:
doSearch(array, m):
length = array.length
last = array[length - 1]
if last == m
return length - 1
array[array.length - 1] = m
index = 0
while array[index] != m
index++
if index == length - 1
array[index] = last
return -1
else
return index经过我们“繁杂的”调整,最终循环的代码少了一次下标判断。如果array的长度很大,比如10000,那么整个循环就可能会减少大量的下标判断语句的执行(m所在的位置越靠后,减少的越多)。而虽然添加了其它一些操作,但是这些代码是和array的长度无关的。这里我们其实就是把m当做了一个哨兵,通过它来删减边界处理。当然,正常情况下,我们不会这样写代码,毕竟可读性真的太差,除非数据量真的很大,又需要追求极致的性能。
五、总结
学习链表最重要的就是理解指针的意义,避免内存泄漏,然后就是多练。而链表作为我们常用的基础数据结构,又要求我们必须对其理解深刻。只有我们真正理解了它的特性,才能将其余实际的业务场景相结合。
注:本文是博主的个人理解,如果有错误的地方,希望大家不吝指出,谢谢