LeetCode145、二叉树的后序遍历（自底向上地思考）

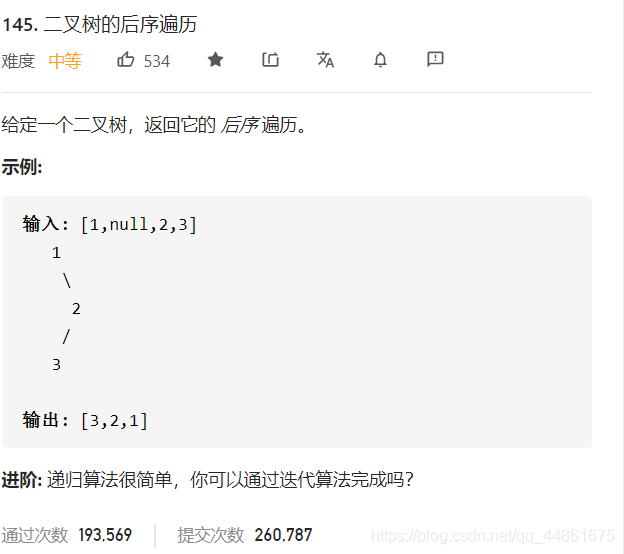
题目描述

145、二叉树的后序遍历

解法

递归——简单

class Solution {
    
    
 List<Integer> list = new ArrayList<>();
 public List<Integer> postorderTraversal(TreeNode root){
    
    
     postorderTraversal(root,list);
     return list;
 }
  public void postorderTraversal(TreeNode root, List<Integer>list){
    
    
      if(root==null) return ;
      postorderTraversal(root.left,list);
      postorderTraversal(root.right,list);
      list.add(root.val);

  } 
}

迭代
二叉树的后序遍历最为复杂难想，难在哪里？

• 因为返回的时候，我们不知道是左孩子的返回还是右孩子的返回
  所以我们必须加一个记录节点。

如果我们能在脑海里面，以自底向下的方式想象递归遍历的过程，我们就比较容易理解它的过程并写出来了：

官方题解版：https://leetcode-cn.com/problems/binary-tree-postorder-traversal/solution/er-cha-shu-de-hou-xu-bian-li-by-leetcode-solution/

就像我们分析前序遍历和中序遍历那样哎：

class Solution {
    
    
    public List<Integer> postorderTraversal(TreeNode root) {
    
    
        List<Integer> res = new ArrayList<Integer>();
        if (root == null) {
    
    
            return res;
        }

        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode prev = null;
        while (root != null || !stack.isEmpty()) {
    
    
            while (root != null) {
    
    
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (root.right == null || root.right == prev) {
    
    
                res.add(root.val);
                prev = root;
                root = null;//这里要注意了，因为我们完成了当前节点访问，所以我们下次从栈顶里面取
            } else {
    
    
                stack.push(root);
                root = root.right;
            }
        }
        return res;
    }
}

自实现版：

class Solution {
    
    
 List<Integer> list = new ArrayList<>();
 public List<Integer> postorderTraversal(TreeNode root){
    
    
     postorderTraversal(root,list);
     return list;

 }
  public void postorderTraversal(TreeNode root, List<Integer>list){
    
    
      if(root==null) return;
        Stack<TreeNode> stack = new Stack<>();//创建一个栈
        TreeNode cur = root;
        TreeNode pre=null;//之前访问的节点

        //左子树入栈：
        while(cur!=null){
    
    
            stack.push(cur);//保证根节点最先入栈
            cur = cur.left;
        }
        while(!stack.isEmpty()){
    
    //栈不空
            cur = stack.pop();//取出当前节点
            //判断当前节点是否此时该被访问：
            if(cur.right!=null && pre != cur.right){
    
    //此时该访问的标志是 没有右子树或者右子树已经被访问
                //还不该访问cur，
                stack.push(cur);//当前节点重新入栈
                cur = cur.right;//开始访问右子树
                while(cur!=null){
    
    
                    //左子树
                    stack.push(cur);//当前根节点最先入栈
                    cur = cur.left;
                }
            }else{
    
    //是该访问cur了
                 list.add(cur.val);
                    //记录已经访问了该节点
                    pre = cur;
            }
        }
    
  }        
}

好好消化，好好体会。