Leetcode101 - 110

其他 2021-03-06 16:27:54 阅读次数: 0

LeetCode 101. 对称二叉树

分析

排除根节点, 分别对左右子树进行递归遍历, 判断是否对称相等.
需要重新写一个函数, 判断是否对称

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    bool isSymmetric(TreeNode* root) {
    
    
        if (!root) return true;
        return dfs(root->left, root->right);
    }
    bool dfs(TreeNode* p, TreeNode* q){
    
    
        if (!p && !q) return true;
        if (!p || !q || p->val != q->val) return false;
        return dfs(p->left, q->right) && dfs(p->right, q->left);
    }
};

迭代写法

对左子树进行 中序遍历, 右子树进行反中序遍历

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
    
    
public:
    bool isSymmetric(TreeNode* root) {
    
    
        if (!root) return true;
        stack<TreeNode*> left, right;
        TreeNode *lc = root->left;
        TreeNode *rc = root->right;
        while(lc || rc || left.size())
        {
    
    
            while (lc && rc)
            {
    
    
                left.push(lc), right.push(rc);
                lc = lc->left, rc = rc->right;
            }
            if (lc || rc) return false; // 如果left.size() != right.size() 那么会在这一步退出.
            lc = left.top(), rc = right.top();
            left.pop(), right.pop();
            if (lc->val != rc->val) return false;
            lc = lc->right, rc = rc->left;
        }
        return true;
    }

};

LeetCode 102. 二叉树的层序遍历

分析

bfs即可

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    vector<vector<int>> levelOrder(TreeNode* root) {
    
    
        vector<vector<int>> res;
        queue<TreeNode*> q;
        if (root) q.push(root);
        while (q.size()){
    
    
            vector<int> level;
            int len = q.size();
            while (len --){
    
    
                auto t = q.front(); q.pop();
                level.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            res.push_back(level);
        }
        return res;
    }
};

LeetCode 103. 二叉树的锯齿形层次遍历

分析

队列中加个变量lcnt即可

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    vector<vector<int>> zigzagLevelOrder(TreeNode* root) {
    
    
        if (!root) return {
    
    };
        vector<vector<int>> res;
        queue<TreeNode*> q;
        q.push(root);
        int lcnt = 1;
        while (q.size()){
    
    
            vector<int> level;
            int len = q.size();
            while (len -- ){
    
    
                auto t = q.front();q.pop();
                level.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            if (lcnt % 2 == 0) reverse(level.begin(), level.end());
            res.push_back(level);
            lcnt ++;
        }
        return res;
    }
};

LeetCode 104. 二叉树的最大深度

分析

考虑根节点到左右儿子节点的距离, 所以根节点的深度 = max(左子树的深度, 右子树的深度) + 1

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    int maxDepth(TreeNode* root) {
    
    
        if (!root) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

LeetCode 105. 从前序与中序遍历序列构造二叉树

分析

需要快速的在中序遍历中找到某个点的位置, 如果遍历的话, 那这一步就是 O ( n ) O(n) O(n), 用Hash表, 可以变成 O ( 1 ) O(1) O(1)在这里插入图片描述

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
    
    
        for (int i = 0; i < inorder.size(); i ++ ) pos[inorder[i]] = i;
        return build(preorder, inorder, 0, preorder.size() - 1, 0, inorder.size() - 1);
    }
    TreeNode* build(vector<int>& preorder, vector<int>& inorder, int pl, int pr, int il, int ir){
    
    
        if (pl > pr) return NULL;
        auto root = new TreeNode(preorder[pl]);
        int k = pos[root->val];
        root->left = build(preorder, inorder, pl + 1, pl + 1 + (k - 1 - il), il, k - 1);
        root->right = build(preorder, inorder, pl + 1 + (k - 1 - il) + 1, pr, k + 1, ir);
        return root;
    }
};

LeetCode 106. 从中序与后序遍历序列构造二叉树

分析

在这里插入图片描述
同上一题

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    unordered_map<int, int> pos;
    TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
    
    
        for (int i = 0; i < inorder.size(); i ++ ) pos[inorder[i]] = i;
        return build(inorder, postorder, 0, inorder.size() - 1, 0, postorder.size() - 1);
    }
    TreeNode* build(vector<int>& inorder, vector<int>& postorder, int il, int ir, int pl, int pr){
    
    
        if (il > ir) return NULL; // 写成pl > pr也可以
        auto root = new TreeNode(postorder[pr]);
        int k = pos[root->val];
        root->left = build(inorder, postorder, il, k - 1, pl, pl + (k - 1 - il));
        root->right = build(inorder, postorder, k + 1, ir, pl + (k - 1 - il) + 1, pr - 1);
        return root;
    }
};

LeetCode 107. 二叉树的层次遍历 II

分析

层序遍历后 直接将res翻转即可

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    vector<vector<int>> levelOrderBottom(TreeNode* root) {
    
    
        if (!root) return {
    
    };
        vector<vector<int>> res;
        queue<TreeNode*> q;
        q.push(root);
        while (q.size()){
    
    
            vector<int> level;
            int len = q.size();
            for (int i = 0; i < len; i ++ ){
    
    
                auto t = q.front(); q.pop();
                level.push_back(t->val);
                if (t->left) q.push(t->left);
                if (t->right) q.push(t->right);
            }
            res.push_back(level);
        }
        reverse(res.begin(), res.end());
        return res;
    }
};

LeetCode 108. 将有序数组转换为二叉搜索树

分析

一般来说, 初始化 直接取线段中点, 然后分别建左子树, 右子树 就可以达到平衡二叉树.

命题 : 1~n为数列, n为线段长度, 取中点, 可以使得两边树平衡

证明: 可以发现节点数为 n n n的一棵满二叉树的高度为 ⌈ log ⁡ 2 ( n + 1 ) ⌉ \lceil \log_2({n + 1})\rceil ⌈log2​(n+1)⌉.
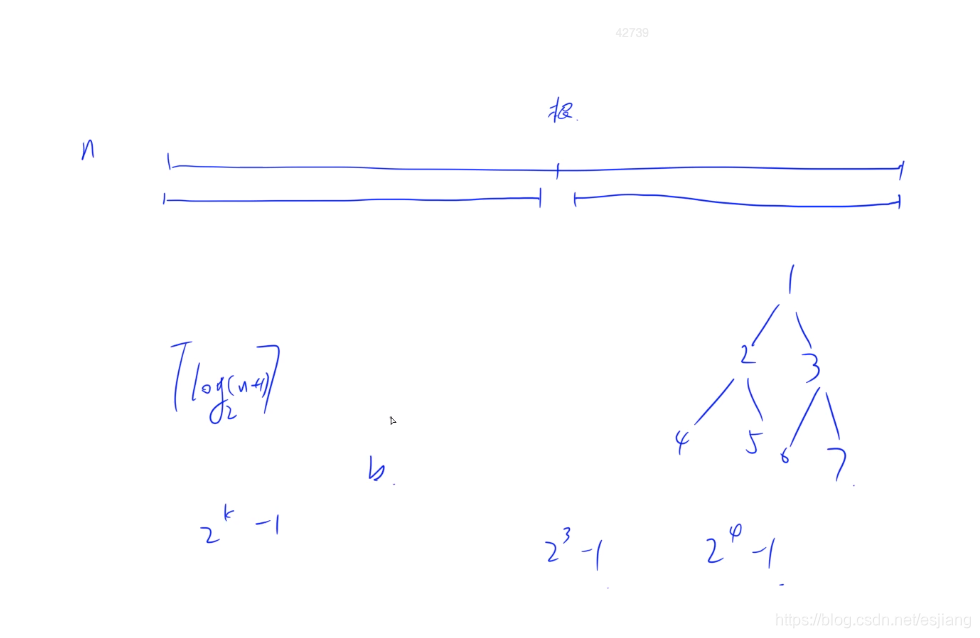
在这里插入图片描述
分两方面来证明,

  1. 因为最理想的情况下, 将n个点按顺序装入树中, 变成满二叉树, 需要 ⌈ log ⁡ 2 ( n + 1 ) ⌉ \lceil \log_2({n + 1})\rceil ⌈log2​(n+1)⌉层.
    因此 二叉树的层数 必须 ≥ ⌈ log ⁡ 2 ( n + 1 ) ⌉ \geq \lceil \log_2({n + 1})\rceil ≥⌈log2​(n+1)⌉.
  2. 数学归纳法, 假设对于 < n <n <n的数列都是成立的, 按照取中点为根节点, 要么左右两边个数是相等, 要么只会差1.
    2.1 如果n是奇数, 左右两边都是 n − 1 2 \frac{n - 1}{2} 2n−1​个数.
    log ⁡ 2 ( n − 1 2 + 1 ) \log_2({\frac{n - 1}{2} + 1)} log2​(2n−1​+1)左右子树高度, + 1因为根节点
    log ⁡ 2 ( n − 1 2 + 1 ) + 1 = log ⁡ 2 n + 1 2 + 1 = log ⁡ 2 n + 1 − log ⁡ 2 2 + 1 = log ⁡ 2 n + 1 \log_2({\frac{n - 1}{2} + 1)} + 1 = \log_2{\frac{n + 1}{2}} + 1 = \log_2{n + 1} - \log_2 2+ 1 = \log_2{n + 1} log2​(2n−1​+1)+1=log2​2n+1​+1=log2​n+1−log2​2+1=log2​n+1
    因此
    ⌈ log ⁡ 2 ( n − 1 2 + 1 ) + 1 ⌉ ≤ ⌈ log ⁡ 2 n + 1 ⌉ \lceil\log_2({\frac{n - 1}{2} + 1)} + 1\rceil \leq \lceil \log_2{n + 1} \rceil ⌈log2​(2n−1​+1)+1⌉≤⌈log2​n+1⌉
    成立.
    2.2 如果n是偶数, 左边: n − 2 2 \frac{n - 2}{2} 2n−2​, 右边 n 2 \frac{n}{2} 2n​, 左边高度 <= 右边高度
    只需证明右边高度 ⌈ log ⁡ 2 ( n + 2 ) ⌉ = ⌈ l o g 2 ( n + 1 ) ⌉ \lceil \log_2({n + 2}) \rceil = \lceil log_2({n + 1})\rceil ⌈log2​(n+2)⌉=⌈log2​(n+1)⌉
    即证明不存在一个数k使得 log ⁡ 2 ( n + 2 ) > k , log ⁡ 2 ( n + 1 ) ≤ k \log_2({n + 2}) > k, \log_2({n + 1}) \leq k log2​(n+2)>k,log2​(n+1)≤k.
    假设存在这样的数k, 使得上式成立, 两边取2的幂次, 得到
    n + 2 > 2 k ≥ n + 1 , 因 为 n 为 偶 数 n + 1 必 定 不 能 取 到 2 k , n + 2 > 2 k > n + 1 n + 2 > 2^k \geq n + 1 , 因为n为偶数 n + 1必定不能取到2^k,\\ n + 2 > 2^k > n + 1 n+2>2k≥n+1,因为n为偶数n+1必定不能取到2k,n+2>2k>n+1
    因为两个整数之间, 不能再插入一个整数, 因此这样的k不存在.

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    TreeNode* sortedArrayToBST(vector<int>& nums) {
    
    
        return build(nums, 0, nums.size() - 1);
    }
    TreeNode* build(vector<int>& nums, int l, int r){
    
    
        if (l > r) return NULL;
        int mid = l + r >> 1;
        auto root = new TreeNode(nums[mid]);
        root->left = build(nums, l, mid - 1);
        root->right = build(nums, mid + 1, r);
        return root;
    }
};

LeetCode 109. 有序链表转换二叉搜索树

分析

两种做法

  1. 将数组push到数组中, 按照上一题来做
  2. 找链表的中点, 递归做, 设链表长度为n, 那么左半段(不带根节点), 且左边不空, 有 ⌈ n − 1 2 ⌉ \lceil \frac{n - 1}{2} \rceil ⌈2n−1​⌉= ⌊ ( n − 1 + 1 ) / 2 ⌋ \lfloor (n - 1+ 1)/ 2 \rfloor ⌊(n−1+1)/2⌋ = ⌊ n 2 ⌋ \lfloor \frac{n}{2} \rfloor ⌊2n​⌋个数, 因此只需要跳 n 2 − 1 \frac{n}{2} - 1 2n​−1步, 可以到达中点的前一个数
  3. 在这里插入图片描述

代码

/**
 * Definition for singly-linked list.
 * struct ListNode {
 *     int val;
 *     ListNode *next;
 *     ListNode() : val(0), next(nullptr) {}
 *     ListNode(int x) : val(x), next(nullptr) {}
 *     ListNode(int x, ListNode *next) : val(x), next(next) {}
 * };
 */
/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    TreeNode* sortedListToBST(ListNode* head) {
    
    
        if (!head) return NULL;
        int n = 0;
        for (auto p = head; p; p = p->next) n ++;
        if (n == 1) return new TreeNode(head->val);
        auto cur = head; // 找中点的前一个点
        for (int i = 0; i < n / 2 - 1; i ++ ) cur = cur->next;
        // 总共n个点, 因为从0开始, n / 2 表示中点的前一个点 , 跳跃的间隔的话需要-1
        auto root = new TreeNode(cur->next->val);
        root->right = sortedListToBST(cur->next->next); // 先建立右子树, 因为cur->next下一步会改成NULL
        cur->next = NULL; // 左边为空的话, 空->next会报错
        // 因此需要保证左边不空, 即左边 上取整[n - 1]个点.
        root->left = sortedListToBST(head);
        return root;
    }
};

LeetCode 110. 平衡二叉树

分析

按照定义, 去判断左右子树的高度, 然后递归左右子树判断平衡树即可
一定要递归isBlanced(root->left) && isBlanced(root->right)

代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
    
    
public:
    bool isBalanced(TreeNode* root) {
    
    
        if (!root) return true;
        return abs(maxDepth(root->left) - maxDepth(root->right)) <= 1 && isBalanced(root->left) && isBalanced(root->right);

    }
    int maxDepth(TreeNode* root){
    
    
        if (!root) return 0;
        return max(maxDepth(root->left), maxDepth(root->right)) + 1;
    }
};

猜你喜欢

转载自blog.csdn.net/esjiang/article/details/114268544
110
今日推荐
周排行
如何设置让双网卡同时工作
mysql数据库安装与卸载
STM32使用J-LINK下载HEX文件
Top 100 HD Love Wallpapers (High Quality)
当prop.load(Utils.class.getClassLoader().getResourceAsStream("jdbc.properties"))一直获取不到资源流要先看看文件路径
leetcode 785. Is Graph Bipartite?
使用GDAL/OGR读写矢量文件
安装Office Visio 提示Office 16 Click-to-Run Extensibility Component
Cookies【ASP.NET】
Python3---高级应用---代理爬虫
每日归档
更多
2025-01-11(0)
2025-01-10(0)
2025-01-09(0)
2025-01-08(0)
2025-01-07(0)
2025-01-06(0)
2025-01-05(0)
2025-01-04(0)
2025-01-03(0)
2025-01-02(0)

代码天地 © 2018 codetd.com

境外服务器   最新电视剧2022