2.1.3 BFS中的双向广搜和A-star

双向广搜

当广搜中间遍历到的范围数量很大的时候，可以采用双向广搜。

AcWing 190. 字串变换

分析

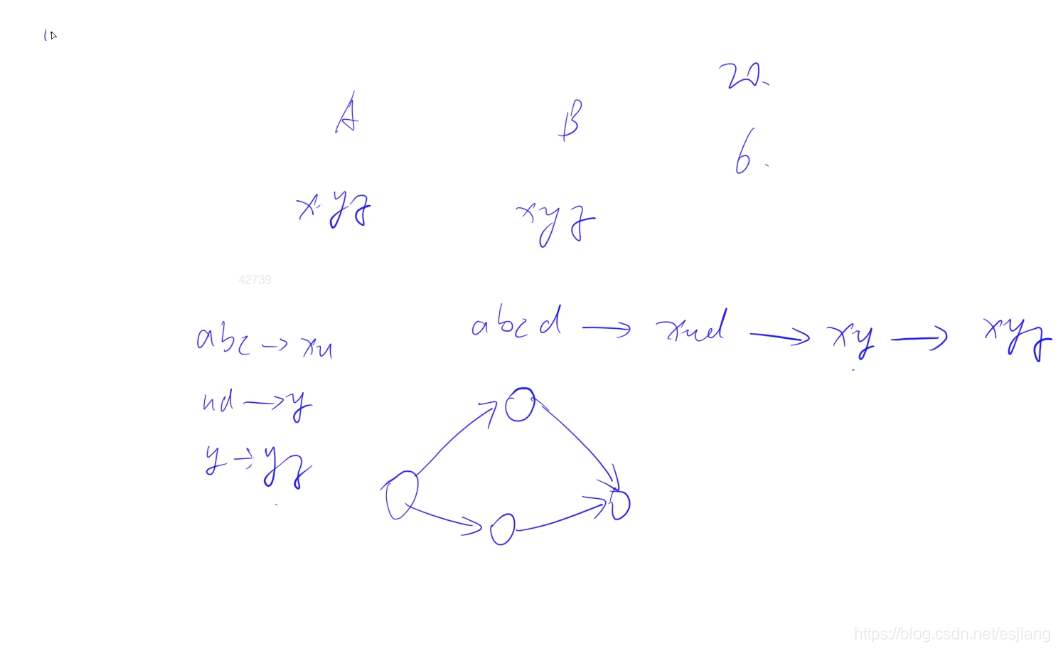
可以把每个字符串看成单独的状态，把所有可以从当前变化到的状态，看成是连接当前点和另外一个状态的边，这样就转化为图论的问题。
问：从A到B最少需要走几步
A,B的长度最多为20，规则有6个。估计下，直接爆搜，整个遍历到的数量有多少。
答案要求10步以内。
字符串从任意起点开始，都可以应用6个规则。20个字符，总共20个起始位置，一个位置可以扩展6个结果，20个位置可以扩展120个结果。最多10步。
总的时间复杂度$120^{10}$，就算假设每次只有一个位置可以往外扩展，也有$6^{10}$

双向广搜效率问题

比如单路扩展，$6^{10}$复杂度，那么双向广搜， 可以降低到$2\ast 6^5$， $6^{10}/2\ast 6^5\approx 3000$. 效果非常好

双向广搜使用范围

用在最小步数模型中, flood fill 和最短路模型，总共搜到的点数量不大。直接搜也不会爆时间。最小步数模型里，一般状态数量是指数级别，这样的话，用双向广搜，可以提高运行效率。

双向广搜写法

傻瓜式

每次从两个方向分别扩展一步

优化式

因为每次从两个方向扩展的空间大小不同，比如从起点扩展出来的空间非常大，但从终点扩展状态比较小。
因此可以选择队列中状态数量较小的方向去扩展，这样实际运行效率较高

代码

#include <iostream>
#include <cstring>
#include <queue>
#include <unordered_map>
using namespace std;
const int N = 6;


int n;
string a[N], b[N]; // 表示 a[i] -> b[i]的规则

int extend(queue<string>& q, unordered_map<string, int>& da, unordered_map<string, int>& db, string a[], string b[]){
    
    
    // 因为队头总是弹出，q.size()每次循环都在变化，而k每次在++，所以要用sk表示初始队列的长度，使得能遍历整个队列
    // 不然的话， q.size() --, k ++, 那就不正确了
    for (int k = 0, sk = q.size(); k < sk; k ++ ){
    
     // 每次需要扩展一层
        string t = q.front(); q.pop();
        
        for (int i = 0; i < t.size(); i ++ )// 枚举从哪个起点应用规则
            for (int j = 0; j < n; j ++ ) // 枚举应用哪个规则
                if (t.substr(i, a[j].size()) == a[j]){
    
    
                    string state = t.substr(0, i) + b[j] + t.substr(i + a[j].size()); // 前面保留 + 中间变化 + 后面保留
                    if (da.count(state)) continue;
                    if (db.count(state)) return da[t] + 1 + db[state];
                    da[state] = da[t] + 1;
                    q.push(state);
                }
    }
    return 11;
}

int bfs(string A, string B){
    
    
    queue<string> qa, qb;
    unordered_map<string, int> da, db;
    qa.push(A), da[A] = 0;
    qb.push(B), db[B] = 0;
    
    while (qa.size() && qb.size()) {
    
    
        int t;
        if (qa.size() <= qb.size()) t = extend(qa, da, db, a, b);
        else t = extend(qb, db, da, b, a);
        if (t <= 10) return t;
    }
    return 11;
}

int main(){
    
    
    string A, B;
    cin >> A >> B;
    while (cin >> a[n] >> b[n]) n ++;
    
    int step = bfs(A, B);
    if  (step > 10) puts("NO ANSWER!");
    else cout << step << endl;
    
    return 0;
}

注意，扩展节点的时候一定要扩展一层

A*

介绍

当搜索的状态空间达到$10^7,10^8$, 甚至$10^{20}$, 可以采用{A*}算法，因为 启发函数减少搜索空间, 求出起点到终点的最短路径了。

因此A*算法不适合 搜索范围比较小的题目（不适合 Flood Fill, 最短路模型）

A*算法步骤

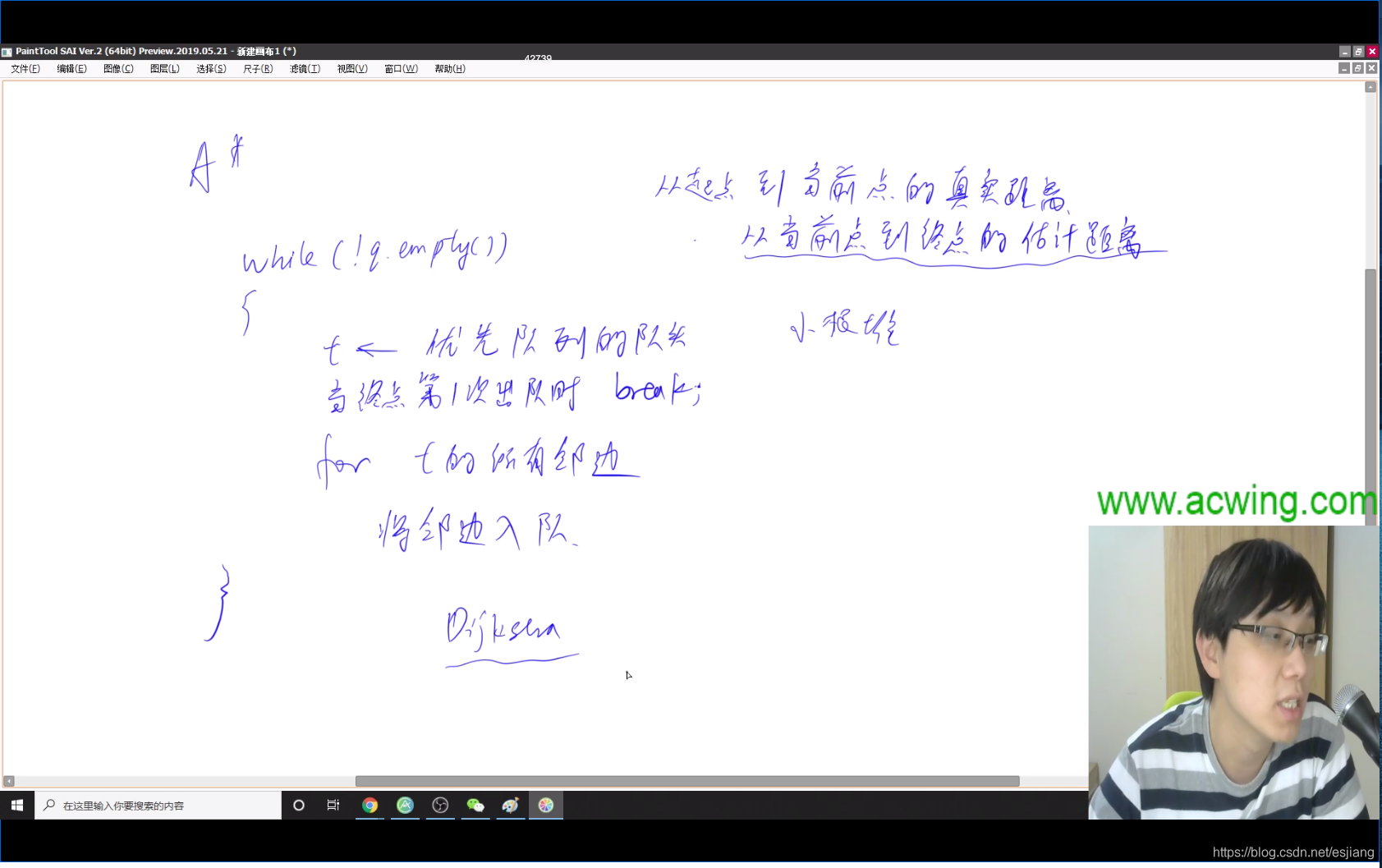
Dijkstra算法可以看成是{A*}算法估价函数为0的特殊情况

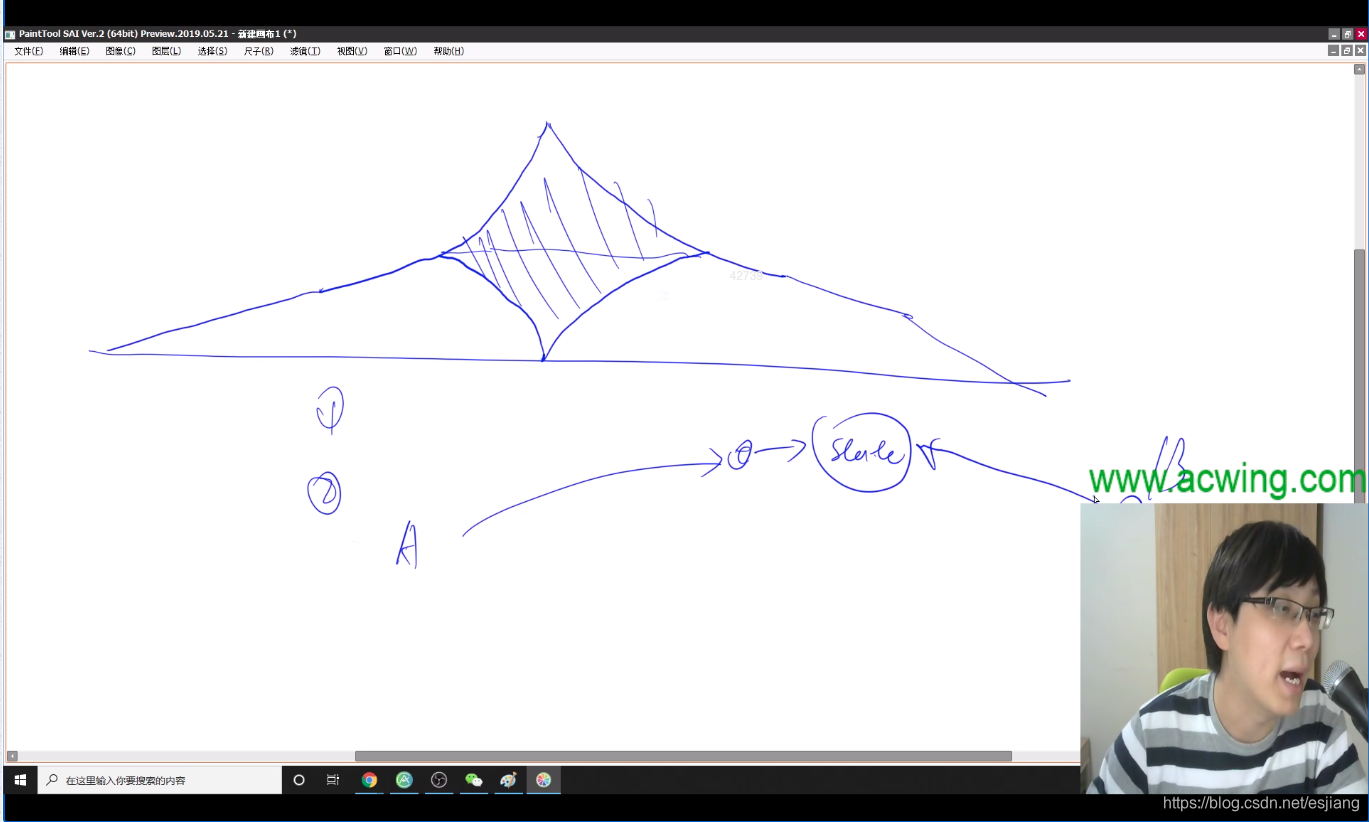
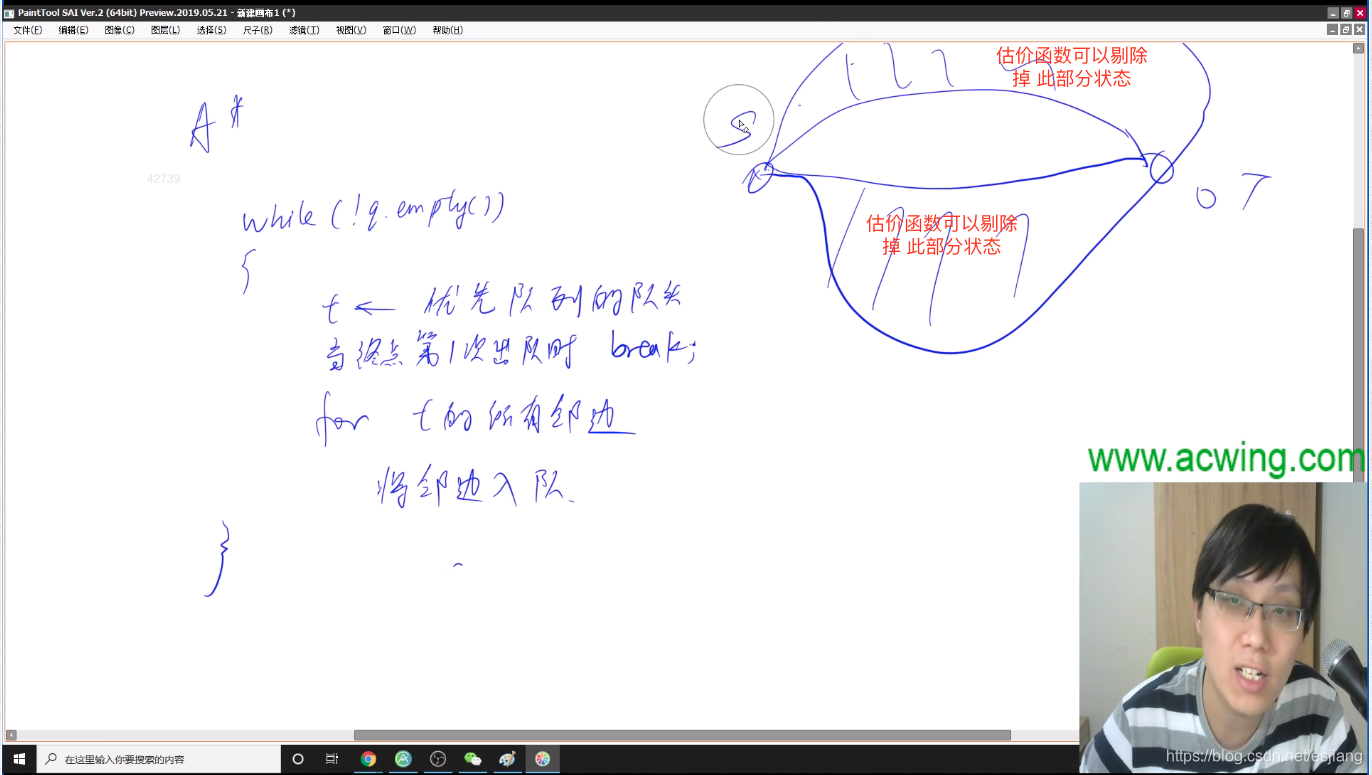
下图中估价函数可以剔除的原因是：这些点到终点的估价函数值非常大，因此可以值搜中间部分，就可以搜到最短距离。

证明：A*算法的正确性

当前状态： d(state)
当前状态到终点的距离： g(state)
当前状态到中间的估价距离：f(state)

条件：f(state) <= g(state)
证明： 假设终点$T$第1次出队时不是最小值（指距离起点的最小值）, 并且当前弹出的元素是T 那么有以下式子成立：
$d_T>d_{最优}........(1)$
在题目有解的情况下, 肯定存在最优路径上的某个点$u$（至少起点在最优路径上）（在优先队列中，还没有被弹出），起点距离该点距离为$d_u$，那么
$d(u)+f(u)\le d(u)+g(u)=d_{最优}......(2)$
结合(1) 和(2) 可以得到以下式子
$d_T > d_{最优} \geq d(u) + f(u) > d(u) $
因此在优先队列中$u$比$T$ 应该先弹出， 与当前是T弹出，矛盾。

重要：

《算法进阶指南》 说每个状态只需要被扩展一次，之后再被取出可以忽略 是错误的。
我们只能保证终点第一次取出，距离起点是最优的距离， 最多只能保证最优路径上的点距离是最优的。

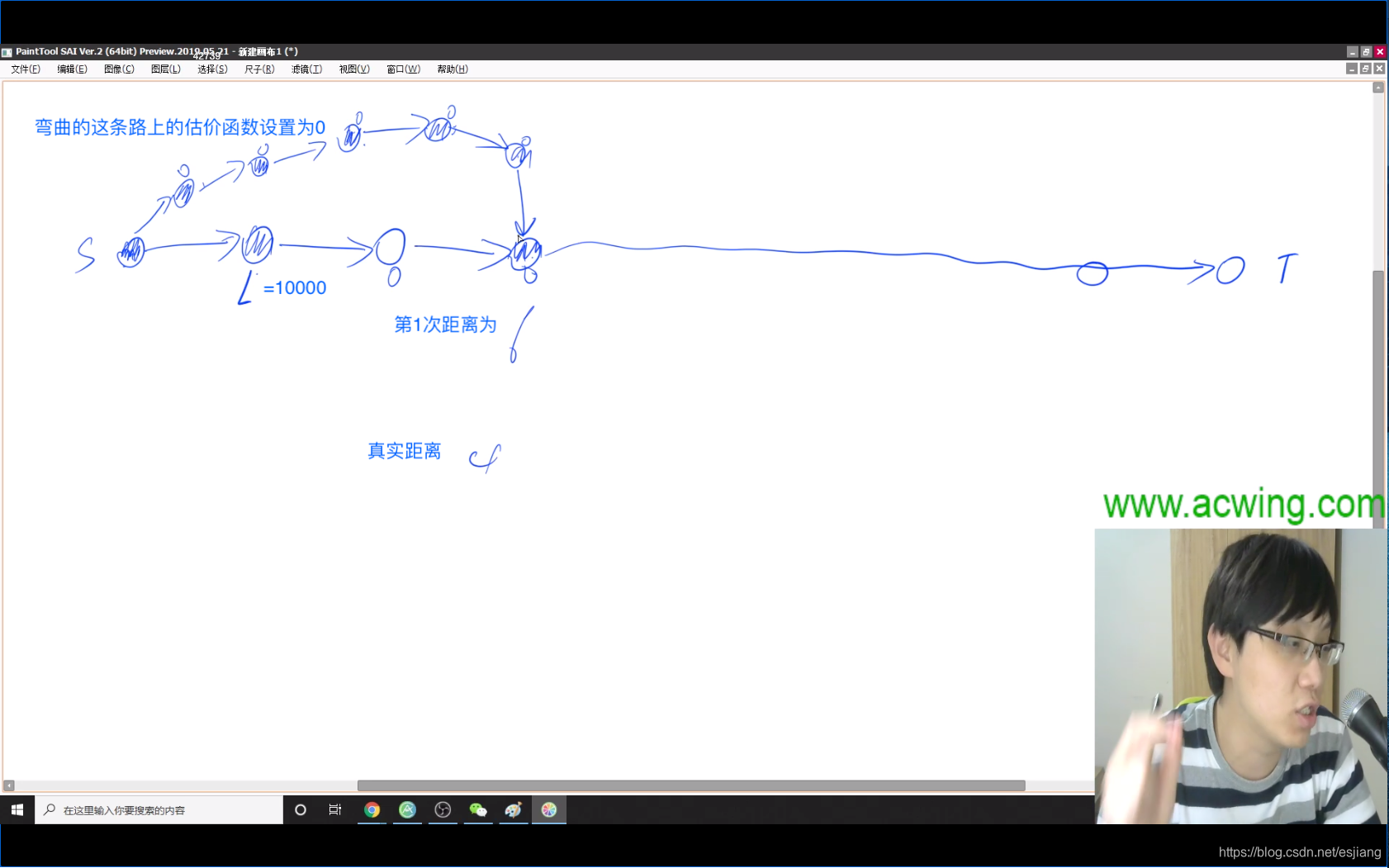
那么为什么最终会得到最优路径呢。
因为按照上面弯曲的路线走，走到后面某一步会发现距离为L + 1, 大于下面这条路径到起点的距离，就会拨乱反正，从下面笔直的路走。
（图中除了估价函数标记为L的点以外，其他点估价函数全取为0）

几个广搜算法的判重

BFS 每次状态只会入队一次，可以在入队的时候，判重,continue 跳过该点
Dijkstra， 说出队的时候，距离是最优的，因此可以在当前点第二次出队的时候continue，跳过该点
{A*}, 出队的时候，也不能判重（只有终点第一次出队，才是正确的），其他点出来一次，更新一次，出来一次，更新一次距离。

估价函数怎么取

一般会有传统的，成熟的取估价函数的方法，如果是一个比较新的问题，只能自己取猜一个 $0\le f()\le g()$。
其中$f$表示估价函数，$g$表示真实距离。

题目不知道有没有解怎么办

{A*}算法只能保证在题目有解的情况可以搜，无解的话，不如朴素bfs, 实际应用中，不能事先知道有解没解，只能硬着头皮去写{A*}， 大部分情况下会比较快。

AcWing 179. 八数码

分析

$i<j,A_i<A_j$称$<A_i,A_j>$为一对逆序对.
有解的必要条件：逆序对为偶数
行内与X(空格交换的话），不改变逆序数。
上下行交换X与其他数，只会影响X与后面的数的逆序对。

估价函数的设计

每次某个数字与X(空格)交换, 最好的情况下会将当前状态与最终状态距离-1.
因此估价函数可以取当前每个数与目标位置之间的曼哈顿距离之和。

代码

#include <iostream>
#include <algorithm>
#include <unordered_map>
#include <queue>
using namespace std;

typedef pair<int, string> PIS;// 1.表示到起点的距离， 2表示当前的状态

int f(string state){
    
    
    int res = 0;
    for (int i = 0; i < state.size(); i ++ )
        if (state[i] != 'x'){
    
    
            int t = state[i] - '1'; // state是一行，  换算距离原点0的距离， 方便转换成3x3
            res += abs(i / 3 - t / 3) + abs(i % 3 - t % 3);
        }
    
    return res;
            
}

string bfs(string start){
    
    
    int dx[] = {
    
    -1, 0, 1, 0}, dy[] = {
    
    0, 1, 0, -1}; // 上右下左方向，不要混乱着写
    char op[4] = {
    
    'u', 'r', 'd', 'l'};
    
    string end = "12345678x";
    unordered_map<string, int> dist;
    unordered_map<string, pair<string, char>> prev;
    priority_queue<PIS, vector<PIS>, greater<PIS>> heap;

    heap.push({
    
    f(start), start});
    dist[start] = 0;
    
    while (heap.size()){
    
    
        auto t = heap.top(); heap.pop();
        
        string state = t.second;
        
        if (state == end) break;
        
        // 注意：heap中元素 第一个参数int是 当前点到起点距离 + 估价函数f，而不是到起点距离dist
    	// 要获得到起点距离，需要从dist中获取。
        int step = dist[state];
        
        int x, y;
        //  取出x的位置
        for (int i = 0; i < state.size(); i ++ )
            if (state[i] == 'x'){
    
    
                x = i / 3, y = i % 3;
                break;
            }
        
        // 与x交换
        string source = state;
        for (int i = 0; i < 4; i ++ ){
    
    
            int a = x + dx[i], b = y + dy[i];
            if (a < 0 || a >= 3 || b < 0 || b >= 3) continue;
            swap(state[x * 3 + y], state[a * 3 + b]);
            // 注意： 第一次搜到!dist.count(state)， 和 后面这种情况都要算进来
            if (!dist.count(state) || dist[state] > step + 1){
    
    
                dist[state] = step + 1;
                prev[state] = {
    
    source, op[i]};
                heap.push({
    
    dist[state] + f(state), state});
            }
            swap(state[x * 3 + y], state[a * 3 + b]);

        }
    }
    
    string res;
    while (end != start){
    
    
        res += prev[end].second;
        end = prev[end].first;
    }
    
    reverse(res.begin(), res.end());
    
    return res;
}

int main(){
    
    
    string g, c, seq;
    while (cin >> c){
    
    
        g += c; // 初始状态
        if (c != "x") seq += c; // 用来计算逆序对的序列， 因为计算逆序对的时候不能带x
    }
    
    //计算逆序对
    int t = 0;
    for (int i = 0; i < seq.size(); i ++ )
        for (int j = i + 1; j < seq.size(); j ++ )
            if (seq[i] > seq[j])
                t ++;
    
    if (t % 2) puts("unsolvable");
    else cout << bfs(g) << endl;
    
    return 0;
}

AcWing 178. 第K短路

分析

因为是求第K短路，考虑如何枚举到所有路线。 即：将当前能扩展到的点全部加入进来。
在求最短路问题中，是将能更新当前点的距离的点加入进来。
这里是第k短路，不仅仅是求最短路！！！，相当于爆搜了

估价函数的选取

估价函数需要选取<= 真实距离，且比较接近
可以选取从该点到终点的最短距离
因为不管以什么样的路线，从当前点到终点的最短距离 一定 >= 从当前点到终点的距离。
因此f()可以取成每个点到终点的最短距离。
可以从反向图上求得该距离。即在反向图上做一遍dijkstra

如何求得第k短路

代码

#include <iostream>
#include <cstring>
#include <queue>
using namespace std;
typedef pair<int, int> PII;
typedef pair<int, PII> PIII; // Astar算法中队列中需要push这个，
// 1.当前点到起点距离 + 估价函数 2.真实距离 3.当前点的编号

#define x first
#define y second

const int N = 1010, M = 200010;

int n, m, S, T, K;
int h[N], rh[N], e[M], w[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int h[], int a, int b, int c){
    
    
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}

void dijkstra(){
    
    
    // memset(st, 0, sizeof st);
    memset(dist, 0x3f, sizeof dist);
    dist[T] = 0;
    
    priority_queue<PII, vector<PII>, greater<PII>> heap;
    heap.push({
    
    0, T});
    
    while(heap.size()){
    
    
        auto t = heap.top(); heap.pop();
        int ver = t.y;
        if (st[ver]) continue;
        st[ver] = true;
        
        for (int i = rh[ver]; ~i; i = ne[i]){
    
    
            int j = e[i];
            if (dist[j] > dist[ver] + w[i]){
    
    
                dist[j] = dist[ver] + w[i];
                heap.push({
    
    dist[j], j});
            }
        }
    }
}

int astar(){
    
    
    priority_queue<PIII, vector<PIII>, greater<PIII>> heap;
    heap.push({
    
    dist[S], {
    
    0, S}});
    
    while (heap.size()){
    
    
        auto t = heap.top(); heap.pop();
        
        int ver = t.y.y, distance = t.y.x;// distance表示起点到当前点的距离， dist[j]表示当前点到终点的距离
        cnt[ver] ++;
        if (cnt[T] == K) return distance;
        
        for (int i = h[ver]; ~i; i = ne[i]){
    
    
            int j = e[i];
            if (cnt[j] < K)
                heap.push({
    
    distance + w[i] + dist[j], {
    
    distance + w[i], j}});
        }
    }
    return -1;
}

int main(){
    
    
    cin >> n >> m;
    memset(h, -1, sizeof h);
    memset(rh, -1, sizeof rh);
    
    while (m -- ){
    
    
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(h, a, b, c), add(rh, b, a, c);
    }
    
    scanf("%d%d%d", &S, &T, &K);
    if (S == T) K ++;
    
    dijkstra();
    
    printf("%d\n", astar());
    
    return 0;
}

代码中if(cnt[ver] < K)的剪枝

yxc ： 对的，这个剪枝在极端情况下可能会有问题，所以这里是对正确性和时间做了下权衡。