*题目编号为Leetcode中对应的题号。
某位大佬的Leetcode题解参考链接
二叉树
-
完全二叉树:除了最后一层,所有层的节点数达到最大,最后一层的所有节点在最左侧。(堆就是二叉树)
-
满二叉树:所有层的节点数达到最大。
-
平衡二叉树:没一个节点的左右子树的高度差不超过1.
-
二分搜索树:每个节点的键值大于左孩子、小于右孩子,以左右孩子为根的子树仍然为二分搜索树。
-
二分搜索树中的一个节点大于其右子树中的所有节点,小于其左子树中的所有节点。
-
具有天然递归条件
// 前序遍历 void preorder(TreeNode* node){ if(node == NULL) // 递归终止条件 return; cout<<node->val<<endl; // 递归过程 preorder(node->left); preorder(node->right); } -
无非是广度优先遍历和深度优先遍历;与高度有关、有路径有关
-
(104二叉树的最大深度) 给定一个二叉树,找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
int maxDepth(TreeNode* root) { if(root==NULL) return 0; int depth_l=0, depth_r=0; if(root->left) depth_l=maxDepth(root->left); if(root->right) depth_r=maxDepth(root->right); return max(depth_l,depth_r)+1; } -
(111二叉树的最小深度) 给定一个二叉树,找出其最小深度。
最小深度是从根节点到最近叶子节点的最短路径上的节点数量。
class Solution { public: int minDepth(TreeNode* root) { if(root == NULL) return 0; if(root->left == NULL && root->right == NULL) return 1; int ret = INT_MAX; if(root->left) ret = min(ret, 1 + minDepth(root->left)); if(root->right) ret = min(ret, 1 + minDepth(root->right)); return ret; } }; -
(226翻转二叉树) 翻转一棵二叉树。
示例:
输入: 4 / \ 2 7 / \ / \ 1 3 6 9 输出: 4 / \ 7 2 / \ / \ 9 6 3 1TreeNode* invertTree(TreeNode* root) { if(root==NULL) return NULL; invertTree(root->left); invertTree(root->right); swap(root->left,root->right); return root; } -
(100相同的二叉树) 给定两个二叉树,编写一个函数来检验它们是否相同。
如果两个树在结构上相同,并且节点具有相同的值,则认为它们是相同的。
class Solution { public: bool isSameTree(TreeNode* p, TreeNode* q) { if(!p && !q) return true; if(!p || !q) return false; if(p->val != q->val) return false; return isSameTree(p->left, q->left) && isSameTree(p->right, q->right); } }; -
(102二叉树的层序遍历)
// 基础层序遍历 // 使用队列实现BFS vector<int> levelOrder(TreeNode* root) { vector<int> ret; if (root == NULL) return ret; queue<TreeNode*> q; q.push(root); while (!q.empty()) { TreeNode* node = q.front(); ret.push_back(node->val); q.pop(); if (node->left) q.push(node->left); if (node->right) q.push(node->right); } return ret; } // 使用队列实现 vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> res; if(root == NULL) return res; queue<pair<TreeNode*,int>> q; q.push(make_pair(root, 0)); while(!q.empty()){ TreeNode* node = q.front().first; int level = q.front().second; q.pop(); if(level == res.size()) res.push_back(vector<int>()); assert( level < res.size() ); res[level].push_back(node->val); if(node->left) q.push(make_pair(node->left, level + 1 )); if(node->right) q.push(make_pair(node->right, level + 1 )); } return res; } // 使用递归实现 class Solution { public: vector<vector<int>> levelOrder(TreeNode* root) { vector<vector<int>> ans; pre(root, 0, ans); return ans; } void pre(TreeNode *root, int depth, vector<vector<int>> &ans) { if (!root) return ; if (depth >= ans.size()) ans.push_back(vector<int>()); ans[depth].push_back(root->val); pre(root->left, depth + 1, ans); pre(root->right, depth + 1, ans); } }; -
(101对称二叉树) 给定一个二叉树,检查它是否是镜像对称的。
// Recursive class Solution { public: bool isSymmetric(TreeNode* root) { if(root == NULL) return true; return is_mirror(root, root); } private: bool is_mirror(TreeNode* root1, TreeNode* root2){ if(root1 == NULL && root2 == NULL) return true; if(root1 == NULL || root2 == NULL) return false; if(root1->val != root2->val) return false; return is_mirror(root1->left, root2->right) && is_mirror(root1->right, root2->left); } }; /// Non-Recursive /// Using two queues to level traverse the root in different directions /// 利用队列实现BFS(层序遍历) /// Time Complexity: O(n) /// Space Complexity: O(n) class Solution { public: bool isSymmetric(TreeNode* root) { if(root == NULL) return true; queue<TreeNode*> q1, q2; q1.push(root); q2.push(root); while(!q1.empty() && !q2.empty()){ TreeNode* node1 = q1.front(); q1.pop(); TreeNode* node2 = q2.front(); q2.pop(); if(node1 == NULL && node2 == NULL) continue; if(node1 == NULL || node2 == NULL) return false; if(node1->val != node2->val) return false; q1.push(node1->left); q1.push(node1->right); q2.push(node2->right); q2.push(node2->left); } return q1.empty() && q2.empty(); } }; -
(222完全二叉树的节点个数) 给出一个完全二叉树,求出该树的节点个数。
示例:
输入: 1 / \ 2 3 / \ / 4 5 6 输出: 6// 常规解法:BFS或DFS // 法一:使用队列进行BFS // 法二:使用DFS class Solution { public: int countNodes(TreeNode* root) { if (root == NULL) return 0; countNodes(root->left); countNodes(root->right); return ++count; } private: int count=0; }; /// Recursion /// Time Complexity: O(h^2) where h is the height of the tree /// Space Complexity: O(h) class Solution { public: int countNodes(TreeNode* root) { if(root == NULL) return 0; int leftLeft = leftHeight(root->left); int leftRight = rightHeight(root->left); if(leftLeft == leftRight) return 1 + ((1<<leftLeft) - 1) + countNodes(root->right); assert(leftLeft == leftRight + 1); return 1 + ((1<<leftRight) - 1) + countNodes(root->left); } private: int leftHeight(TreeNode* root){ if(root == NULL) return 0; return 1 + leftHeight(root->left); } int rightHeight(TreeNode* root){ if(root == NULL) return 0; return 1 + rightHeight(root->right); } }; -
(110平衡二叉树) 给定一个二叉树,判断它是否是高度平衡的二叉树。
示例:
3 / \ 9 20 / \ 15 7 返回true 1 / \ 2 2 / \ 3 3 / \ 4 4 返回falseclass Solution { public: bool isBalanced(TreeNode* root) { return height(root) != -1; } // 返回树的高度 -1为不平衡 int height(TreeNode* root){ if(root == nullptr) return 0; int left = height(root->left); if(left == -1) return -1; int right = height(root->right); if(right == -1) return -1; return abs(left - right) > 1 ? -1 : 1 + max(left, right); } }; -
(404左叶子之和) 计算给定二叉树的所有左叶子之和。
示例:
3 / \ 9 20 / \ 15 7 在这个二叉树中,有两个左叶子,分别是 9 和 15,所以返回 24class Solution { private: int res = 0; public: int sumOfLeftLeaves(TreeNode* root) { if(!root) return 0; dfs(root, false); return res; } private: void dfs(TreeNode* node, bool isLeft){ if(!node->left && !node->right){ if(isLeft) res += node->val; return; } if(node->left) dfs(node->left, true); if(node->right) dfs(node->right, false); } }; -
(257二叉树的所有路径) 给定一个二叉树,返回所有从根节点到叶子节点的路径。
输入: 1 / \ 2 3 \ 5 输出: ["1->2->5", "1->3"] 解释: 所有根节点到叶子节点的路径为: 1->2->5, 1->3vector<string> binaryTreePaths(TreeNode* root) { vector<string> res; if(root == NULL) return res; // 如果是叶子节点 if(root->left == NULL && root->right == NULL){ res.push_back(to_string(root->val)); return res; } // 找到左子树的所有路径 vector<string> leftPaths = binaryTreePaths(root->left); for(int i = 0 ; i < leftPaths.size() ; i ++) res.push_back(to_string(root->val) + "->" + leftPaths[i]); // 找到右子树的所有路径 vector<string> rightPaths = binaryTreePaths(root->right); for(int i = 0 ; i < rightPaths.size() ; i ++) res.push_back(to_string(root->val) + "->" + rightPaths[i]); return res; } // 存储为数组 vector<vector<int>> binaryTreePaths2(TreeNode* root) { vector<vector<int>> ret; if (root == NULL) return ret; vector<int> tres; dfs(root, tres, ret); return ret; } void dfs(TreeNode* node, vector<int>& tres, vector<vector<int>>& ret) { tres.push_back(node->val); if (!node->left && !node->right) ret.push_back(tres); if (node->left) dfs(node->left, tres, ret); if (node->right) dfs(node->right, tres, ret); tres.pop_back(); return; } -
(112路径总和) 给定一个二叉树和一个目标和,判断该树中是否存在根节点到叶子节点的路径,这条路径上所有节点值相加等于目标和。
示例:
给定如下二叉树,以及目标和sum = 22,5 / \ 4 8 / / \ 11 13 4 / \ \ 7 2 1返回
true, 因为存在目标和为 22 的根节点到叶子节点的路径5->4->11->2。bool hasPathSum(TreeNode* root, int sum) { if(root==NULL) return false; if(root->val==sum && !root->left && !root->right) return true; if(root->left && hasPathSum(root->left, sum-root->left->val)) return true; if(root->right && hasPathSum(root->right, sum-root->right->val)) return true; return false; } // 法二: bool hasPathSum(TreeNode* root, int sum) { if (root == NULL) return false; return dfs(root, 0, sum); } bool dfs(TreeNode* node, int tsum, int sum) { tsum += node->val; if (!node->left && !node->right) { if (tsum == sum) return true; } if (node->left && dfs(node->left, tsum, sum)) return true; if (node->right && dfs(node->right, tsum, sum)) return true; tsum -= node->val; return false; } -
(113路径总和II) 给定一个二叉树和一个目标和,找到所有从根节点到叶子节点路径总和等于给定目标和的路径。
示例
给定如下二叉树,以及目标和 sum = 22,5 / \ 4 8 / / \ 11 13 4 / \ / \ 7 2 5 1返回:
[ [5,4,11,2], [5,8,4,5] ]class Solution { public: vector<vector<int>> pathSum(TreeNode* root, int sum) { vector<vector<int>> res; if(!root) return res; vector<int> tres; dfs(root, tres, 0, sum, res); return res; } private: void dfs(TreeNode* node, vector<int>& tres, int tsum, int sum, vector<vector<int>>& res){ tres.push_back(node->val); tsum += node->val; if(!node->left && !node->right){ if(tsum == sum) res.push_back(tres); } if (node->left) dfs(node->left, tres, tsum, sum, res); if (node->right) dfs(node->right, tres, tsum, sum, res); tres.pop_back(); return; } }; -
(129求根到叶子节点数字之和) 给定一个二叉树,它的每个结点都存放一个
0-9的数字,每条从根到叶子节点的路径都代表一个数字。例如,从根到叶子节点路径1->2->3代表数字123。计算从根到叶子节点生成的所有数字之和。
示例:
输入: [1,2,3] 1 / \ 2 3 输出: 25 解释: 从根到叶子节点路径 1->2 代表数字 12. 从根到叶子节点路径 1->3 代表数字 13. 因此,数字总和 = 12 + 13 = 25. 输入: [4,9,0,5,1] 4 / \ 9 0 / \ 5 1 输出: 1026 解释: 从根到叶子节点路径 4->9->5 代表数字 495. 从根到叶子节点路径 4->9->1 代表数字 491. 从根到叶子节点路径 4->0 代表数字 40. 因此,数字总和 = 495 + 491 + 40 = 1026.class Solution { public: int sumNumbers(TreeNode* root) { if(!root) return 0; int res = 0; dfs(root, 0, res); return res; } private: void dfs(TreeNode* node, int tnum, int& sum){ tnum = tnum * 10 + node->val; if(!node->left && !node->right) sum += tnum; else{ if(node->left) dfs(node->left, tnum, sum); if(node->right) dfs(node->right, tnum, sum); } } }; -
(437 路径总和III) 给定一个二叉树,它的每个结点都存放着一个整数值。找出路径和等于给定数值的路径总数。路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。二叉树不超过1000个节点,且节点数值范围是 [-1000000,1000000] 的整数。
示例:root = [10,5,-3,3,2,null,11,3,-2,null,1], sum = 8 10 / \ 5 -3 / \ \ 3 2 11 / \ \ 3 -2 1 返回 3。和等于 8 的路径有: 1. 5 -> 3 2. 5 -> 2 -> 1 3. -3 -> 11 -
(235 二分搜索树的最近公共祖先) 给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。
例如,给定如下二叉搜索树: root = [6,2,8,0,4,7,9,null,null,3,5]
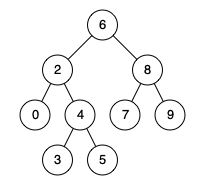
示例:
输入: root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
输出: 6
解释: 节点 2 和节点 8 的最近公共祖先是 6。
说明:
-
所有节点的值都是唯一的。
-
p、q 为不同节点且均存在于给定的二叉搜索树中。
// 定义:在以root为根节点的二分搜索树中,找到节点p和q的最近公共祖先节点 TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root==NULL || p==NULL || q==NULL) return NULL; //if((root->val>p->val && root->val<q->val) || (root->val<p->val && root->val>q->val)) // return root; //if(root->val==p->val || root->val==q->val) // return root; if(root->val>p->val && root->val>q->val) return lowestCommonAncestor(root->left, p, q); if(root->val<p->val && root->val<q->val) return lowestCommonAncestor(root->right, p, q); return root; }
-
(98验证二分搜索树) 给定一个二叉树,判断其是否是一个有效的二叉搜索树。
// 中序遍历一颗二分搜索树将得到一个有序数组 class Solution { public: bool isValidBST(TreeNode* root) { vector<int> vec; inOrder(root, vec); for(int i = 1 ; i < vec.size() ; i ++) if(vec[i-1] >= vec[i]) return false; return true; } private: void inOrder(TreeNode* node, vector<int>& vec){ if(node == NULL) return; inOrder(node->left, vec); vec.push_back(node->val); inOrder(node->right, vec); } }; // 递归版 class Solution { public: bool isValidBST(TreeNode* root) { return isValidBST(root, INT_MIN, INT_MAX); } private: bool isValidBST(TreeNode* node, int min, int max){ if(node == NULL) return true; if(node->val < min || node->val > max) return false; if(node->left != NULL && node->left->val >= node->val) return false; if(node->right != NULL && node->right->val <= node->val) return false; return isValidBST(node->left, min, node->val - 1) && isValidBST(node->right, node->val + 1, max); } }; -
(450删除二分搜索树中的节点) 给定一个二叉搜索树的根节点 root 和一个值 key,删除二叉搜索树中的 key 对应的节点,并保证二叉搜索树的性质不变。返回二叉搜索树(有可能被更新)的根节点的引用。
示例:
root = [5,3,6,2,4,null,7] key = 3 5 / \ 3 6 / \ \ 2 4 7 给定需要删除的节点值是 3,所以我们首先找到 3 这个节点,然后删除它。 一个正确的答案是 [5,4,6,2,null,null,7], 如下图所示。 5 / \ 4 6 / \ 2 7 另一个正确答案是 [5,2,6,null,4,null,7]。 5 / \ 2 6 \ \ 4 7class Solution { public: TreeNode* deleteNode(TreeNode* root, int key) { if(!root) return NULL; if(key < root->val){ root->left = deleteNode(root->left, key); return root; } if(key > root->val){ root->right = deleteNode(root->right, key); return root; } if(!root->right) return root->left; if(!root->left) return root->right; TreeNode* p = root, *minnode = root->right; while(minnode->left){ p = minnode; minnode = minnode->left; } root->val = minnode->val; root->right = deleteMinNode(root->right); return root; } private: TreeNode* deleteMinNode(TreeNode* root){ if(!root->left) return root->right; root->left = deleteMinNode(root->left); return root; } }; -
(108将有序数组转换为二分搜索树) 将一个按照升序排列的有序数组,转换为一棵高度平衡二叉搜索树。
示例:
给定有序数组: [-10,-3,0,5,9], 一个可能的答案是:[0,-3,9,-10,null,5],它可以表示下面这个高度平衡二叉搜索树: 0 / \ -3 9 / / -10 5class Solution { public: TreeNode* sortedArrayToBST(vector<int>& nums) { if(nums.size() == 0) return NULL; return buildTree(nums, 0, nums.size() - 1); } private: TreeNode* buildTree(const vector<int>& nums, int l, int r){ if(l > r) return NULL; if(l == r) return new TreeNode(nums[l]); int mid = (l + r) / 2; TreeNode* root = new TreeNode(nums[mid]); root->left = buildTree(nums, l, mid - 1); root->right = buildTree(nums, mid + 1, r); return root; } }; -
(230二分搜索树中第k小的元素) 给定一个二叉搜索树,编写一个函数
kthSmallest来查找其中第 k 个最小的元素。示例:
输入: root = [3,1,4,null,2], k = 1 3 / \ 1 4 \ 2 输出: 1// 中序遍历 class Solution { private: int index; public: int kthSmallest(TreeNode* root, int k) { index = 0; return kthSmallestNode(root, k)->val; } private: TreeNode* kthSmallestNode(TreeNode* node, int k){ if(node == NULL) return NULL; TreeNode* res = kthSmallestNode(node->left, k); if(res) return res; index ++; if(index == k) return node; return kthSmallestNode(node->right, k); } }; -
(236二叉树中的最近公共祖先) 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
// 找到两条路径 class Solution { public: TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { vector<TreeNode*> path1; dfs(root, p, path1); vector<TreeNode*> path2; dfs(root, q, path2); TreeNode* res; for(int i = 0; i < path1.size() && i < path2.size(); i ++) if(path1[i] == path2[i]) res = path1[i]; else break; return res; } private: bool dfs(TreeNode* node, TreeNode* target, vector<TreeNode*>& path){ if(!node) return false; path.push_back(node); if(node == target) return true; if(dfs(node->left, target, path)) return true; if(dfs(node->right, target, path)) return true; path.pop_back(); return false; } }; // 递归版 class Solution { public: // 在root中寻找p和q // 如果p和q都在root所在的二叉树中, 则返回LCA // 如果p和q只有一个在root所在的二叉树中, 则返回p或者q // 如果p和q均不在root所在的二叉树中, 则返回NULL TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) { if(root == NULL) return root; if(root == p || root == q) return root; TreeNode *left = lowestCommonAncestor(root->left, p, q); TreeNode *right = lowestCommonAncestor(root->right, p, q); if(left != NULL && right != NULL) return root; if(left != NULL) return left; if(right != NULL) return right; return NULL; } };