Excel安装&线性回归
一、Excel安装
1、Excel下载
方案一
自行百度进行下载,这里为大家附上下载链接
我在网上下了很多次,安装的时候就变成了WPS的兼容安装,试了很多次都是一样的,然后我就问老师要了相关安装包。
据说安装后与WPS兼容的解决方法为:
- 默认打开方式为WPS;
- 鼠标右键选择,用Excel打开。
我也没有去试,然后就直接安装老师发来的安装包。
方案二
我将安装包放到百度网盘,供大家自行下载。
链接:https://pan.baidu.com/s/13zalik-bfq1KrxsUurpLdw
提取码:l5pb
https://pan.baidu.com/s/13zalik-bfq1KrxsUurpLdw .
2、Excel安装
下载好安装包后,找到文件所在位置并右击鼠标,以管路员身份运行;

开始安装

等待安装…

安装完成

会在桌面出现如图三个快捷方式。
二、线性回归实例
实例1会为大家附上详细的教程,如何利用Excel对数据进行线性回归分析,后面的实例则直接显示结果
1、认识线性回归
回归
回归是设法找出变量间在数量上的依存变化关系, 用函数表达式表达出来,这个表达式称之为回归方程。
两变量间的关系
- 确定性关系
两变量间的函数关系
圆的周长与半径的关系: C=2R
速度、时间与路程的关系:L=ST
X与Y的函数关系: Y=a+bX - 非确定性关系
两变量在宏观上存在关系,但并未精确到可以用函数关系来表达。
青少年身高与年龄的关系;
身高与体重的关系:标准体重(kg)=身高(cm)-105
药物浓度与反应率的关系
线性回归的概念
当两个变量存在准确、严格的直线关系时,可以用Y=a+bX,表示两者的函数关系。
其中X 为自变量(independent variable);Y是因变量( dependent variable )。
但在实际生活当中,由于其它因素的干扰,许多双变量之间的关系并不是严格的函数关系,不能用函数方程来准确反映,为了区别于两变量间的函数方程,我们称这种关系为回归关系,用直线方程来表示这种关系称为回归直线或线性回归。
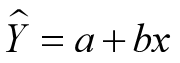
2、Excel线性回归实例1(附详细教程)
由于第一次使用Excel,这里并没有对数据进行线性回归分析,仅仅是利用已有数据对Excel的练手。
双击打开Excel

进入界面后出现如下提示,不用管,直接叉掉

看到如下界面

选择空白工作簿,双击打开

实例一题目PPT截图

PPT散点图

PPT回归方程

b的意义

a的意义

估计值 y^ 的意义

以上都是PPT上内容,下面为实践操作内容
根据例题讲x,y对应数据填入Excel表格

选中x,y值的数据区,点击“插入”——“折线图”——“二维折线图”;

散点图

鼠标右键单击折现,选择“添加趋势线”

选择“线性”、“显示公式”复选框后。点击“关闭”;


就这样,线性回归方程式就完成了

此外,我们还可以通过鼠标右键设置折线的颜色、字体、粗细等

以上就是对Excel绘制图像的简单介绍,后续则是本篇文章的主题。
3、一元线性回归——年龄与心率
添加数据分析项(请看图示步骤)
“文件”——“选项”——“加载项”


点击工具栏“数据”——“数据分析”

在弹出的小窗里面找到回归

单击输入值后面的按钮,注意x,y对应

点击“X”,输入区域会有值填入
对x进行同理操作,选中线性拟合图

注: x,y的行列数须相同,并且输入值要大于等于2
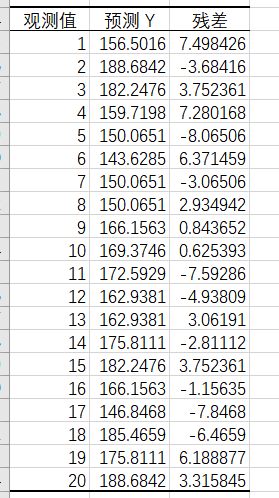
数据分析展示

预测值与残差
数据全部录入后图像(散点图)

鼠标选中坐标轴,可以改变坐标轴的起始值。
将图像作适当调整后

鼠标右击,更改图像类型,换为折线图


折线图如下

通过与PPT对比,拟合直线方程两者雷同,其他数据方面差距也不是很大,可以忽略不计的误差。
三、总结与参考资料
1、总结
由于第一次接触Excel,对于其很多用处都是百度着慢慢学的。不过这个软件对于数据分析相关还是挺方便的,对于线性回归类而言,就不需要如以前一样靠公式去进行复杂的计算了。对于Excel的更多应用,在后面慢慢学,希望这篇文章对大家有所帮助。