特征工程 — 特征选择Filter、Wrapper、Embedded

特征衍生和特征选择是工作中比较耗时的部分 .  

特征工程

特征选择 (feature_selection)

Filter

1. 移除低方差的特征 (Removing features with low variance)

2. 单变量特征选择 (Univariate feature selection)

Wrapper

1. 递归特征消除 (Recursive Feature Elimination)

Embedded

1. 使用SelectFromModel选择特征 (Feature selection using SelectFromModel)

2. 将特征选择过程融入pipeline (Feature selection as part of a pipeline)

当数据预处理完成后，我们需要选择有意义的特征输入机器学习的算法和模型进行训练。

根据不同的数据，选择上面三种方法的其中一种去执行操作。

 

Filter

1） 移除低方差的特征 

如果特征方差比较小，说明这个特征维度上，每个样品区分度不高

移除低方差的特征。因为方差为0，说明一组数据中每个数都是一样的，
那么数据的波动就最小，也就是没有波动了，因为平均数是1，每个数据也都是1
如果一个特征不发散，例如方差接近于0，也就是说样本在这个特征上基本上没有差异，
这个特征对于样本的区分并没有什么用。

from sklearn.feature_selection import VarianceThreshold 传入方差的阈值，低于这个阈值的特征会被移除掉。
threshold 临界点
VarianceThreshold 方差阈值
方差很小，分子很小，说明数值-平均数的太相近，数据太过集中，拥有这些特征无法判断结果。
所以需要移除方差是0的特征还有方差特别小的特征。

from sklearn.feature_selection import VarianceThreshold
X = [[0, 0, 1], [0, 1, 0], [1, 0, 0], [0, 1, 1], [0, 1, 0], [0, 1, 1]]
sel = VarianceThreshold(threshold=(.3 * (1 - .3)))
sel.fit_transform(X)
#当方差低于这个门槛的话会被删掉。保留方差大于这个门槛的特征。
'''
array([[0, 1],
       [1, 0],
       [0, 0],
       [1, 1],
       [1, 0],
       [1, 1]])

'''

import pandas as pd
pd.DataFrame(X)
#第一列大部分都是0，有一个是1，所以被去掉.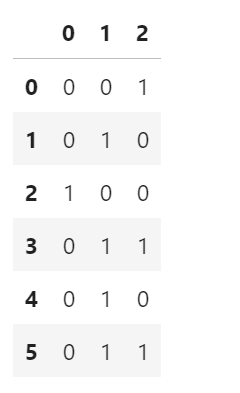

---

 

2）单变量特征选择 (Univariate feature selection)

单变量特征选择的原理是分别单独的计算每个变量的某个统计指标，根据该指标来判断哪些变量重要，剔除那些不重要的变量。()

—根据特征的相关性，选择和目标值的相关性比较强的特征¶

目标是连续值 皮尔逊

目标是离散值 chi卡方检验

对于分类问题(y离散)，可采用：

• 卡方检验

对于回归问题(y连续)，可采用：

• 皮尔森相关系数

• f_regression,

• mutual_info_regression

• 最大信息系数

这种方法比较简单，易于运行，易于理解，通常对于理解数据有较好的效果（但对特征优化、提高泛化能力来说不一定有效）。

• SelectKBest 移除得分前 k 名以外的所有特征(取top k)

• SelectPercentile 移除得分在用户指定百分比以后的特征(取top k%)

• 对每个特征使用通用的单变量统计检验： 假正率(false positive rate) SelectFpr, 伪发现率(false discovery rate) SelectFdr, 或族系误差率 SelectFwe.

• GenericUnivariateSelect 可以设置不同的策略来进行单变量特征选择。同时不同的选择策略也能够使用超参数寻优，从而让我们找到最佳的单变量特征选择策略。

卡方(Chi2)检验

卡方检验就是检验两个变量之间有没有关系。
以运营为例:
卡方检验可以检验男性或者女性对线上买生鲜食品有没有区别；
不同城市级别的消费者对买SUV车有没有什么区别；
如果有显著区别的话，我们会考虑把这些变量放到模型或者分析里去。

卡方检验就是统计样本的实际观测值与理论推断值之间的偏离程度，
实际观测值与理论推断值之间的偏离程度就决定卡方值的大小，如果卡方值越大，二者偏差程度越大；
反之，二者偏差越小；若两个值完全相等时，卡方值就为0，表明理论值完全符合。
注意：卡方检验针对分类变量。

from sklearn.datasets import load_iris
from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
iris = load_iris()
X, y = iris.data, iris.target
X.shape
#(150, 4)

#参数1 使用卡方检验来进行特征选择 K=2，选择最好的两个特征
X_new = SelectKBest(chi2, k=2).fit_transform(X, y)
X_new.shape
#(150, 2)

Pearson相关系数 (Pearson Correlation)¶

皮尔森相关系数是一种最简单的，能帮助理解特征和响应变量之间关系的方法，该方法衡量的是变量之间的线性相关性， 结果的取值区间为[-1，1]，-1表示完全的负相关，+1表示完全的正相关，0表示没有线性相关.

import numpy as np
from scipy.stats import pearsonr
np.random.seed(0)
#seed()被设置了之后，np,random.random()可以按顺序产生一组固定的数组，
#如果使用相同的seed()值，则每次生成的随机数都相同
size = 300
x = np.random.normal(0, 1, size)
# pearsonr(x, y)的输入为特征矩阵和目标向量，能够同时计算 相关系数 和p-value.
print("Lower noise", pearsonr(x, x + np.random.normal(0, 1, size)))
print("Higher noise", pearsonr(x, x + np.random.normal(0, 10, size)))
#Lower noise (0.7182483686213841, 7.324017312998504e-49)
#Higher noise (0.05796429207933814, 0.31700993885325246)

Wrapper 递归特征消除 (Recursive Feature Elimination) RFE

递归消除特征法使用一个基模型来进行多轮训练，每轮训练后，移除若干权值系数的特征，再基于新的特征集进行下一轮训练。

对特征含有权重的预测模型(例如，线性模型对应参数coefficients)，RFE通过递归减少考察的特征集规模来选择特征。首先，预测模型在原始特征上训练，每个特征指定一个权重。之后，那些拥有最小绝对值权重的特征被踢出特征集。如此往复递归，直至剩余的特征数量达到所需的特征数量。

RFECV 通过交叉验证的方式执行RFE，以此来选择最佳数量的特征：对于一个数量为d的feature的集合，他的所有的子集的个数是2的d次方减1(包含空集)。指定一个外部的学习算法，比如SVM之类的。通过该算法计算所有子集的validation error。选择error最小的那个子集作为所挑选的特征。

• 原理，用算法模型反复迭代，利用训练的数据去预测，选择可以返回特征权重的算法（随机森林，逻辑回归)
• 反复迭代 每一次去除一个特征，去除一个用剩下的特征再次训练
• 可以用一个模型来进行特征选择，用另一个模型来做最终过的预测

下面案例，用递归特征消除，选择随机森林处理这个数据：

from sklearn.feature_selection import RFE #递归特征消除
from sklearn.ensemble import RandomForestClassifier #随机森林
from sklearn.datasets import load_iris
#建立一个决策树模型
rf = RandomForestClassifier()
#加载鸢尾花的数据
iris=load_iris()
X,y=iris.data,iris.target
#创建RFE,递归删除特征 对象，传入要进行RFE使用到的模型
rfe = RFE(estimator=rf, n_features_to_select=2) #rfe是递归特征处理问题的方法。
#estimator=rf传入用的估计器是什么.
#n_features_to_select,最终剩下几个数据，2剩下两个数据，跑两次。
X_rfe = rfe.fit_transform(X,y)
X_rfe.shape
#(150, 2)

上面利用训练的数据去预测，选择可以返回特征权重的算法，此数据使用随机森林去实现的。
————————————————————————————————————————————————————————————————————————————————————————————
最终如果用逻辑回归做分类的话，可以用决策树做特征选择。
最终结果要求有可解释性，那就用逻辑回归；特征选择的过程用xgboost或者lightgbm（可解释性差）。

#查看框架的前五行，所有列
X_rfe[:5,:]
'''
array([[1.4, 0.2],
       [1.4, 0.2],
       [1.3, 0.2],
       [1.5, 0.2],
       [1.4, 0.2]])

'''

Embeded

• 利用l1正则做特征选择 基于L1的特征选择 (L1-based feature selection)¶
• xgboost lightgbm 可以输出feature_importance

使用L1范数作为惩罚项的线性模型(Linear models)会得到稀疏解：大部分特征对应的系数为0。
当你希望减少特征的维度以用于其它分类器时，可以通过 feature_selection.SelectFromModel 来选择不为0的系数。

特别指出：常用于此目的的稀疏预测模型有linear_model.lasso(回归)，linear_model.LogisticRegression和svm.LinearSVC（分类）

from sklearn.feature_selection import SelectFromModel 
#SelectFromModel（根据重要性权重选择特征）
from sklearn.svm import LinearSVC
#LinearSVC实现了线性分类支持向量机，
#它在惩罚和损失函数的选择方面具有更大的灵活性，并且应该更好地扩展到大量样本。
lsvc = LinearSVC(C=0.01, penalty="l1", dual=False).fit(X,y)
#penalty默认是L2，这里做替换；利用l1正则训练模型
#运行一次就可以把不重要的去掉
model = SelectFromModel(lsvc, prefit=True)
#把模型 交给SelectFromModel 把l1之后系数为0的特征去掉
X_embed = model.transform(X)
X_embed.shape
#(150, 3)

————————————————————————————————————————————————————————————————
L1正则处理之后，好多系数都变成了0，通过特征选择把系数是0的筛选掉。
L2正则把不太重要的特征系数减小，减到很小，让它对最终结果的影响比较小。

X_embed[:5,:]
'''
array([[5.1, 3.5, 1.4],
       [4.9, 3. , 1.4],
       [4.7, 3.2, 1.3],
       [4.6, 3.1, 1.5],
       [5. , 3.6, 1.4]])
'''