1 问题
老师想给孩子们分发糖果，有 N 个孩子站成了一条直线，老师会根据每个孩子的表现，预先给他们评分。
你需要按照以下要求，帮助老师给这些孩子分发糖果：
每个孩子至少分配到 1 个糖果。
相邻的孩子中，评分高的孩子必须获得更多的糖果。
那么这样下来，老师至少需要准备多少颗糖果呢？
示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。
第三个孩子只得到 1 颗糖果，这已满足上述两个条件。
2 解法
这道题目一定是要确定一边之后，再确定另一边，例如比较每一个孩子的左边，然后再比较右边，「如果两边一起考虑一定会顾此失彼」。
先确定右边评分大于左边的情况（也就是从前向后遍历）
只要右边评分比左边大，右边的孩子就多一个糖果
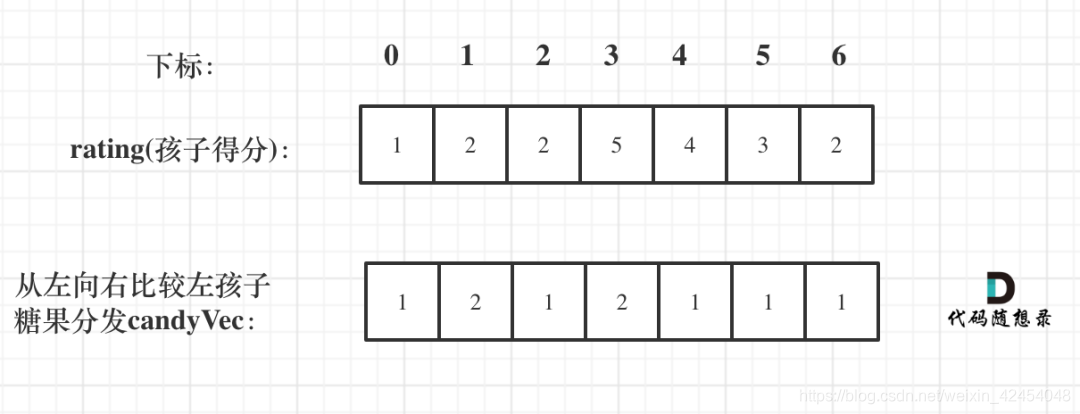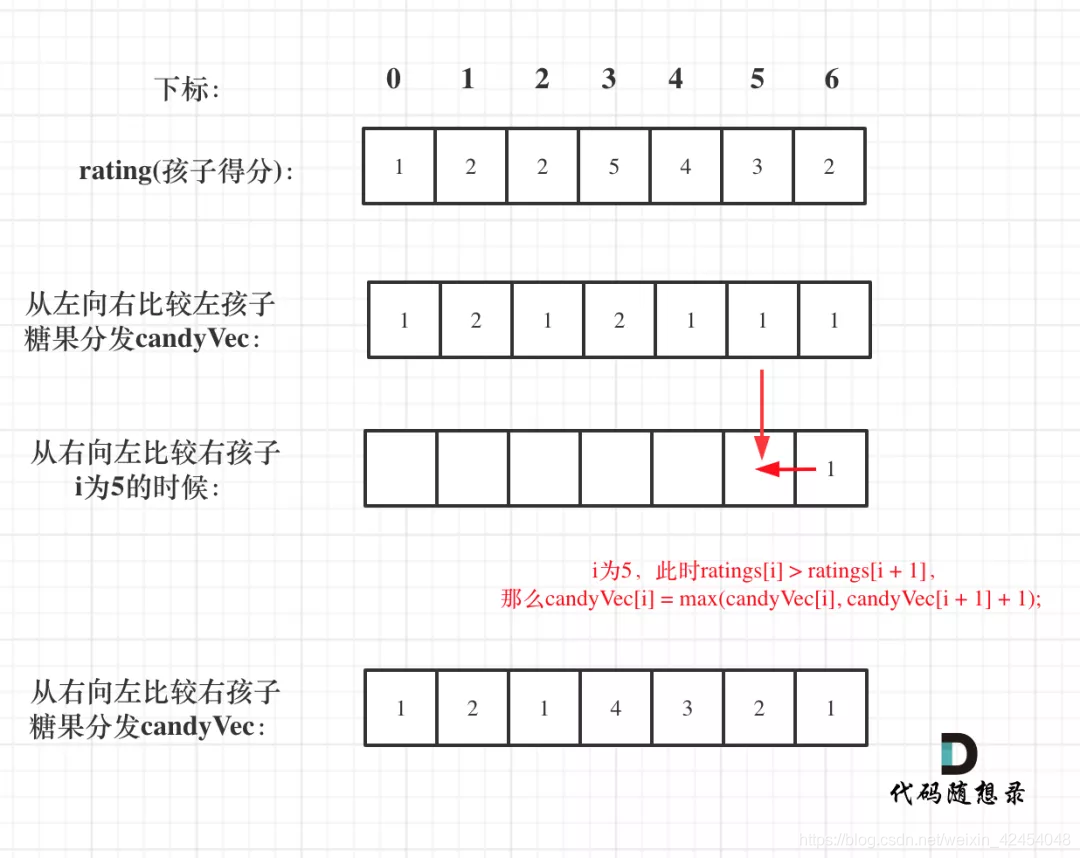
再确定左孩子大于右孩子的情况（从后向前遍历）
如果 ratings[i] > ratings[i + 1]，此时candyVec[i]（第i个小孩的糖果数量）就有两个选择了，一个是candyVec[i + 1] + 1（从右边这个加1得到的糖果数量），一个是candyVec[i]（之前比较右孩子大于左孩子得到的糖果数量）。取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量，保证第i个小孩的糖果数量即大于左边的也大于右边的。
class Solution {
public:
int candy(vector<int>& ratings) {
//初始化结果数组，保证每人至少一颗糖
vector<int> res(ratings.size(), 1);
//从左往右遍历，处理右侧大于左侧的情况
for(int i = 1; i < ratings.size(); i++)
{
if(ratings[i] > ratings[i - 1]) //右 > 左
res[i] = res[i - 1] + 1;
}
//从右往左遍历，处理左侧大于右侧的情况
for(int j = ratings.size() - 2; j >= 0; j--)
{
if(ratings[j] > ratings[j + 1]) //左 > 右
{
//取j左右两侧大的那个
res[j] = max(res[j], res[j + 1] + 1);
}
}
//统计糖果和
int sum = 0;
for(int i = 0; i < res.size(); i++)
sum += res[i];
return sum;
}
};