1.多元线性回归
实例引入：假如我们现在要去预测本地房子的价格，那么我们该怎么办？影响房价的因素有很多：房子面积、方位、地理位置、本地居民收入、房龄等等，很自然的办法就是将这些主要因素纳入，建立一个多元数学模型，从而进行预测。
多元线性回归模型：
Y——我们要得到的结果，随机变量，称因变量；
—— p个非随机变量，是自变量。
是未知参数，称回归系数；ε 是均值为0，方差为
的随机变量，代表随机因素对Y的影响。
总体
的n组观测值
满足下式：
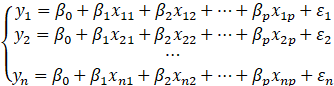
其中，
，才能求出所有回归系数；误差系数
相互独立。
上述线性方程组可以写成矩阵形式：
记
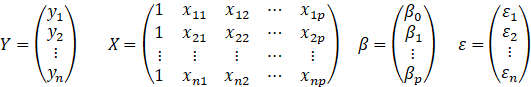
建立多元线性回归模型的基本步骤如下：
①分析问题，选择因变量和自变量，作出二者的散点图，初步设定多元线性回归模型的参数个数。
②输入因变量与自变量的观测值，计算参数估计。
③分析数据的异常点情况。
④作显著性检验，若通过，则对模型作预测。
⑤对模型进一步研究，如残差的正态性检验、残差的异方差检验、残差的自相关性检验等。
2.多元多项式回归
一般地，多元二项式回归模型可表示为：
其步骤与多元线性回归类似，但在作散点图时，一般是可以看到单个变量与随机因变量之间无明显线性关系。
回归方法可以利用MATLAB的Rstool(x,y,’model’,alpha)来进行。