1.5 卷积步长
在之前的介绍中,当在一个nn的图像使用ff的过滤器进行卷积时,位于nn的图像中会有(n+2p-f+1)个和ff过滤器相对应的ff的蓝色区域,逐一卷积得到(n+2p-f+1)(n+2p-f+1) 的图像。
这里介绍的是带步长的卷积。也即是蓝色区域不再是相邻,而是间隔一个步长去进行卷积。

注意当分子不能被分母整除时,需要做的是向下取整。因为f*f的过滤器必须完全放在原图像上。

按照数学定义,上述提到的“卷积”并不是卷积操作,而是属于交叉相关。数学意义上的卷积操作,需要对卷积核进行翻转。在计算机视觉领域中也称交叉相关为卷积操作。
1.6 三维卷积
上几节介绍在二维维度上实现卷积操作,本节介绍三维的卷积 。 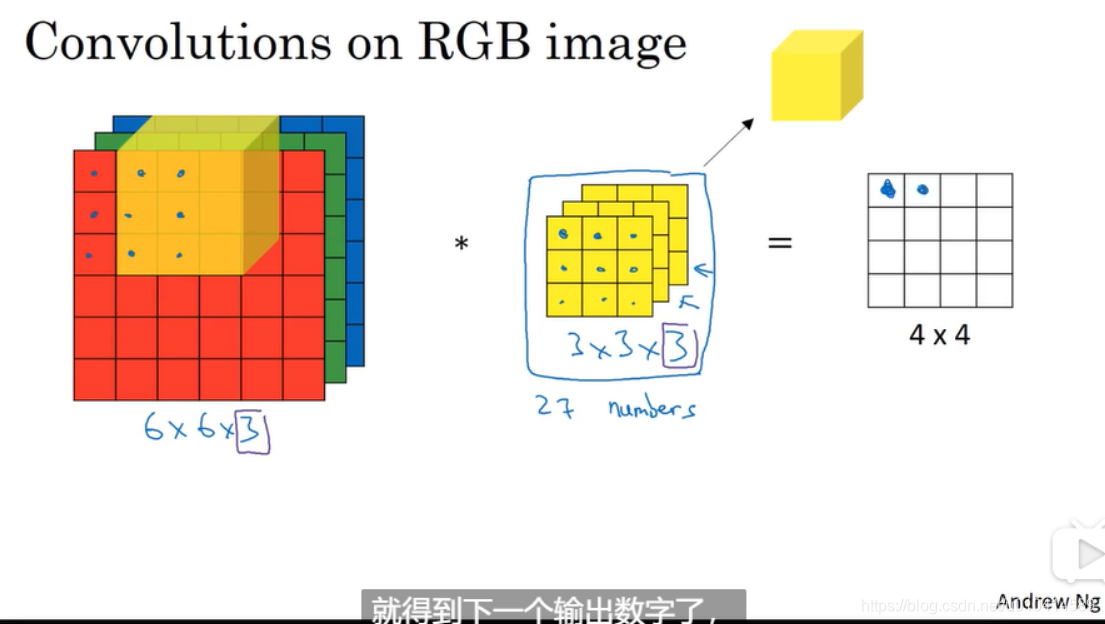
注意通道数量需要和过滤器的通道数量保持一致。另外输出结果中通道数量变为1.
三维的卷积过程,我们可以把过滤器理解为立方体,它有9*3=27个参数,拿这个立方体去逐一和三维的原始图像对应的区域做卷积。
我们可以给过滤器设置一组参数,让它成为一个特定的过滤器。
也就是说如果我们想检测图片中红色通道的边缘,我们可以设置过滤器如下:

如果不在意一个垂直边缘属于哪个颜色,可以设置过滤器如下,这样可以检测出任意颜色的边缘。

也即是通过设置不同的参数,可以从这个333的过滤器中得到不同特征的检测器。
多种检测器
如果我们想同时检测垂直边缘和水平边缘,又或者是75度边缘,也即是我们想同时应用多个过滤器。应用如何做呢?

这里我们就可以应用多个过滤器。需要注意的是原始图像的通道数和过滤器的通道数需要保持一致,最后得到的图像442的2不是通道数,而是应用的过滤器的个数。当我们应用了10个过滤器,就会是4410.
1.7 单层卷积网络
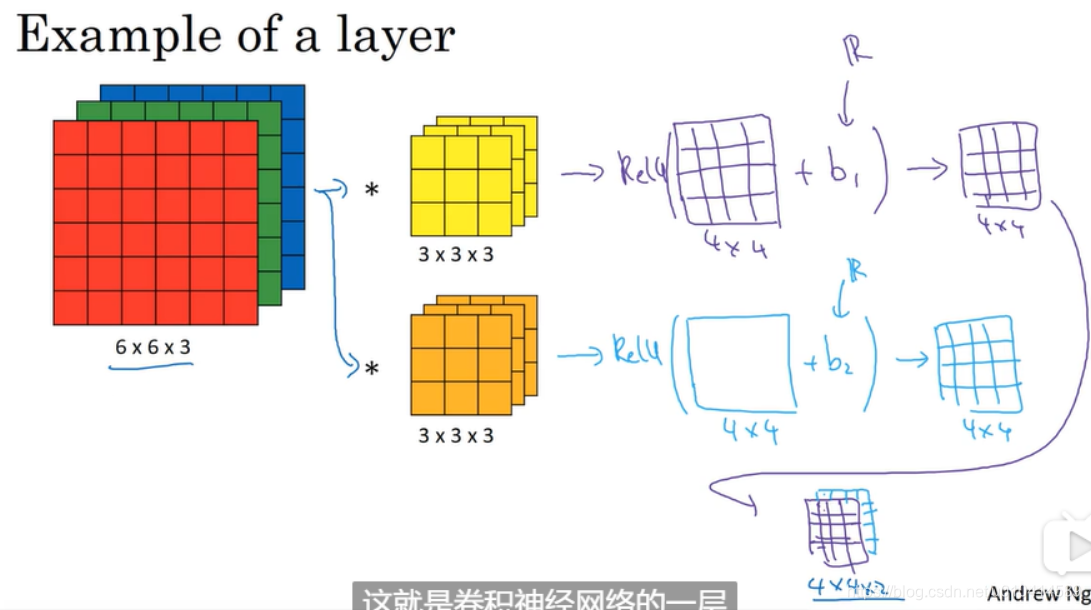
我们对663的图像通过333的过滤器进行卷积操作,每个过滤器会得到一个4*4的输出。最终我们需要把这些输出变成单层卷积神经网络。还需要对每个输出加上一个偏置,并做非线性转换(如RELU)。
我们把这个例子和普通的非卷积单层前向传播神经网络进行对应。
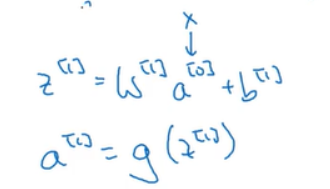
这里的输入就是a0, 这里的过滤器和w1类似,卷积的过程也是对应元素相乘并求和,做的是线性计算。然后也是添加偏置并做非线性转换。
这里卷积计算有一个很好的特性,不管输入图像的大小,只要过滤器的大小和个数固定后,权重参数的个数就是不变的。这样的特性不容易过拟合。
总结

1.8 简单卷积网络示例

最后一步只是将上一层的输出展开成为一个非常长的矢量,然后输送到softmax或者logistics中。
通常来说随着网络的深度的增加,图像的长和宽会逐渐变小,这个例子中也是由39到37到17到7,而通道数通常会逐渐递增,这里是由3到10到20到40。
在一个卷积神经网络中通常有三种类型的层:
- 卷积层Convolution,通常表示为conv
- 池化层Pooling,通常表示为pool
- 全连接层Fully connected,通常表示为FC
1.9 池化层
卷积神经网络还会使用池化层来减少展示量,以提高运算速度。并使一些特征的检测功能更强大。
最大池化
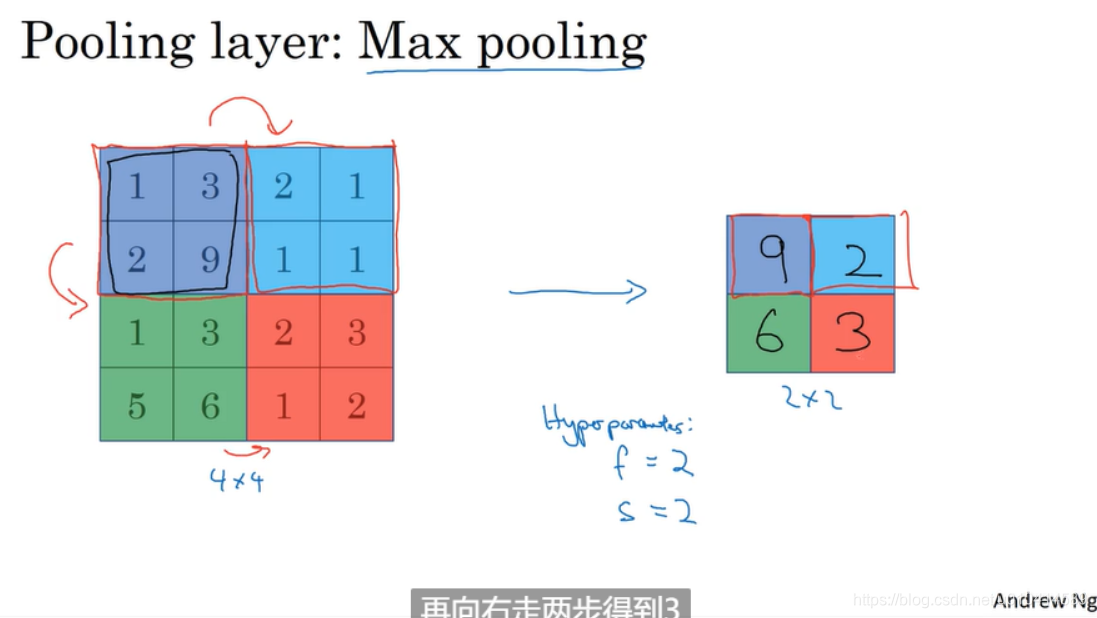
这个过程如同使用了一个2*2的过滤器,使用的步长为2, (这两个值属于Max pooling的超参数)。
max pooling 背后的机理是如果在滤波器中任何地方检测到了这些特征,就保留最大的特征值。(Ng也说大家使用max pooling 主要原因还是因为它的效果很好,或许大家并不真正了解它真正好的原因)
Max pooling 还有一个特性是虽然有一套默认的超参数,但并没有任何需要梯度算法学习的东西。一旦确定了过滤器大小f和步长s,就确定了计算过程,而且梯度下降算法不会对其有任何改变。

上图是另一个组超参数的例子。
三维的Max pooling
如果有三维输入,比如552,过滤器为332, 那么它的输出就是332。这里输出也是和输入的通道个数一致,是因为采样是独立应用于每一个通道。
1.10 卷积神经网络示例
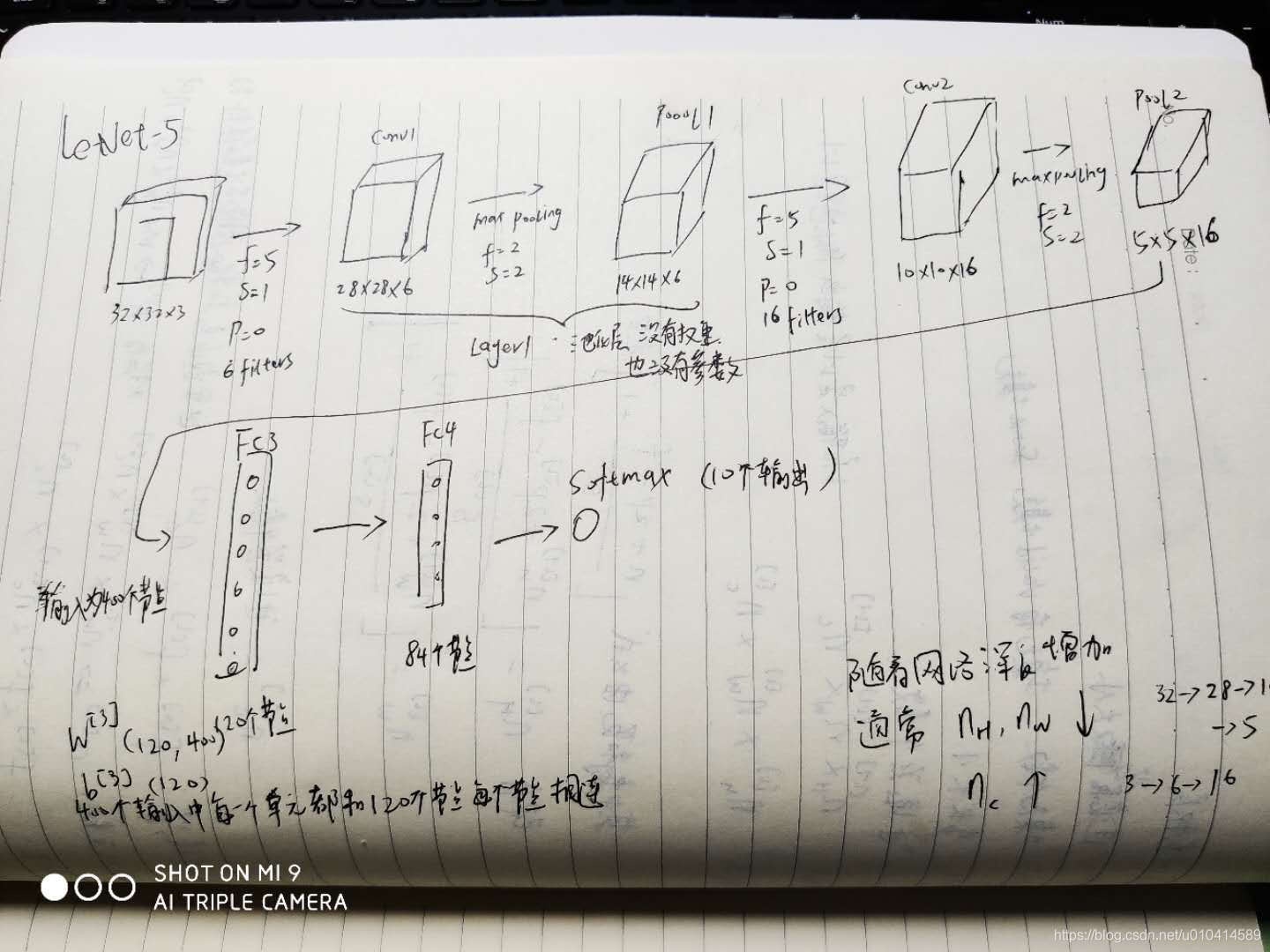
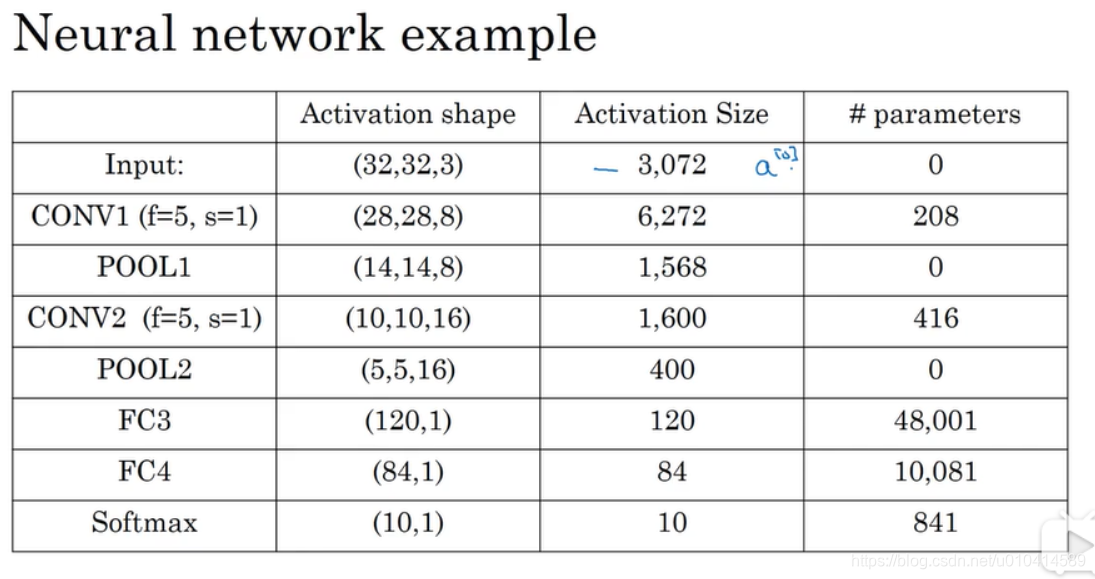
这里需要注意几点:
- 卷积层的参数计算:第一层参数个数为(5*5+1)8 = 208;第二层卷积层参数个数为(55+1)*16=416
- 最大池化没有任何参数;
- 卷积层趋向比较少的参数,绝大多数参数是在全连接层上。
- 随着神经网络的深入,激活输入的大小也逐渐变小。但减少的太快,也不利用网络性能。
1.11 为什么要用卷积
使用卷积相比完全连接的神经网络层,有两个优势:
-
参数共享;
-
连接的稀疏性
下面以一个例子来介绍。
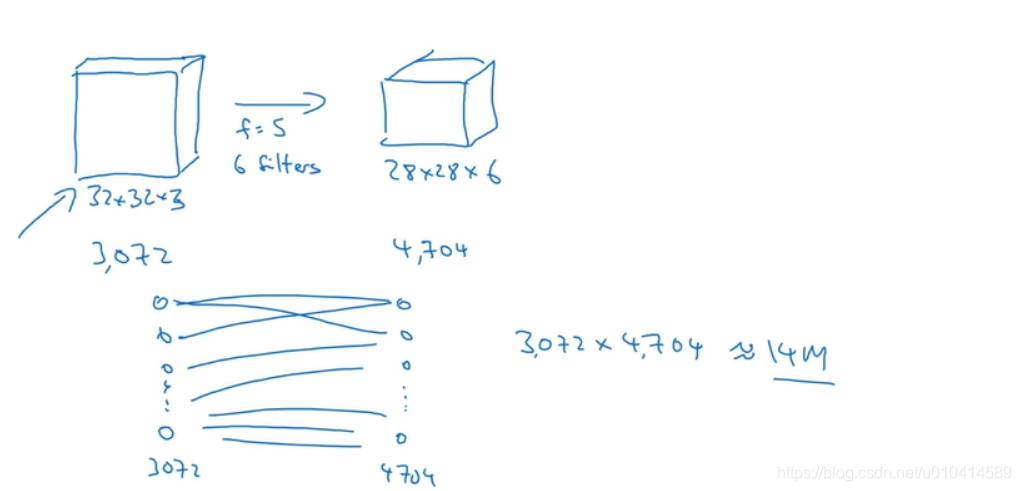
在上一节的例子中,输入层的节点数为32323=3072个,第一个卷积层的节点数为28286,=4704,如果按照完全连接的方式,就是4704*3072 大约1400万个参数。考虑到这个图像的大小还很小,就已经是如此多的参数需要训练。如果图像很大,则权重矩阵会更大。
而采用卷积层,使用556的过滤器,仅需要(5*5+1)*6 = 156个参数。
而卷积层参数少的原因有俩个:
- 参数共享。参数共享是源于在特征检测器中,例如垂直边缘检测器对图像的一部分是有用的,那么对于另一部分也可能是有用的。
2.稀疏链接。在每一层中,每一个输出仅仅依赖一小部分输入数据。其他的数据对这个输出不会产生影响。
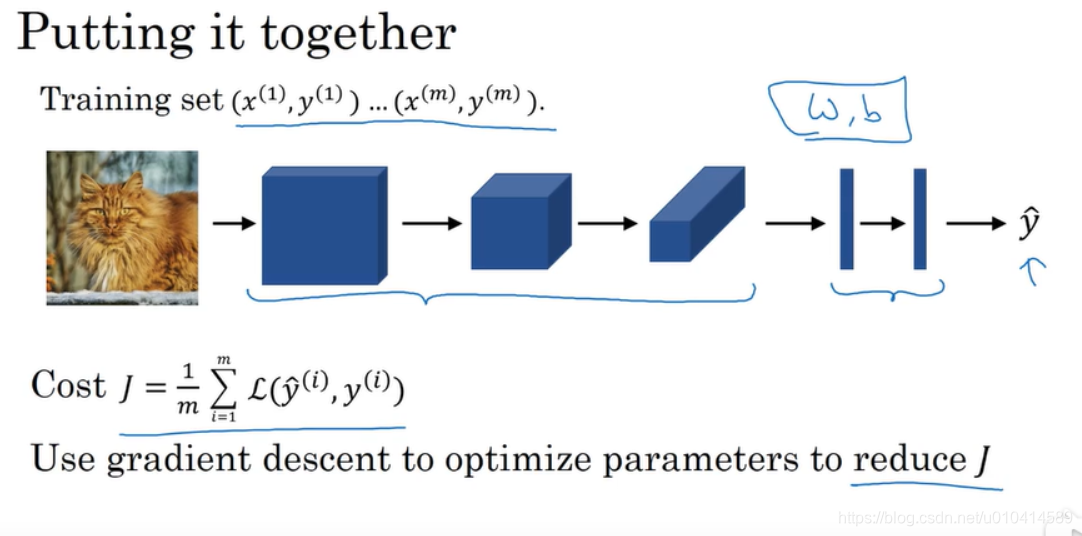
现在总结一下如何训练一个卷积神经网络。
首先有一个训练数据集。
然后我们设计了一个卷积神经网络结构,包括输入层、卷积层、池化层、全连接层,输出层。
在这个过程中,我们会有各个层的参数W和B
同样会定义一个成本函数Cost J
我们随机初始化W和B,然后使用随机梯度下降等类似的算法去优化成本函数J。
经过一定的迭代,我们就会得到一个很好的检测模型。