先试试看原先的遍历方法:

测试:出现死循环。

因为原先的8号节点的左右指针是空的,这也是结束遍历的条件。
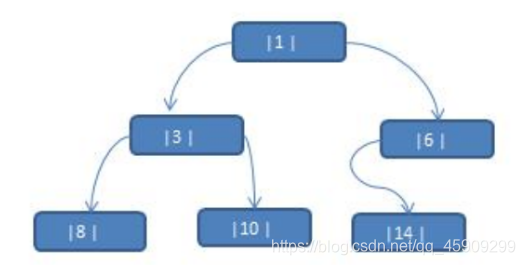
但在线索化之后,这个结束条件就不成立了。所以,退不出去,就进入了死循环。
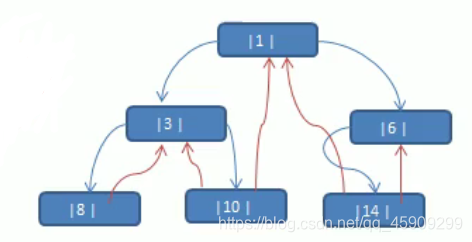
综上:当线索化二叉树后,不能再使用原来的遍历方法。
分析:由于线索化之后,各个节点指向有变化 ,因此原来的遍历方式不能使用,这时需要使用新的方式遍历线索化二叉树,各个节点可以通过线性方式遍历,因此无需使用递归方式,这样也提高了遍历的效率。遍历的次序应和中序遍历保持一致。
接上文:
会有疑问,例如:拿什么来区分节点指向的是左子树,还是前驱节点呢?
这就需要用到HeroNode中我们写的规定了:

核心代码:
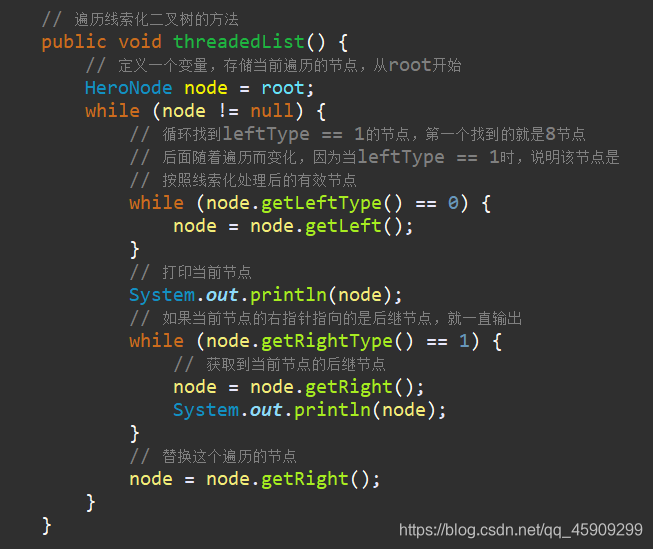
测试:

前序、后序。先挖个坑,有空回来再填。
中序线索化二叉树及遍历的完整代码:
package com.huey.tree.threadedbinarytree;
public class ThreadedBinaryTreeDemo {
public static void main(String[] args) {
// 测试中序线索二叉树的功能
HeroNode root = new HeroNode(1, "tom");
HeroNode node2 = new HeroNode(3, "jack");
HeroNode node3 = new HeroNode(6, "smith");
HeroNode node4 = new HeroNode(8, "mary");
HeroNode node5 = new HeroNode(10, "king");
HeroNode node6 = new HeroNode(14, "dim");
// 二叉树,后面递归创建,现在简单处理使用手动创建
root.setLeft(node2);
root.setRight(node3);
node2.setLeft(node4);
node2.setRight(node5);
node3.setLeft(node6);
// 测试中序线索化
ThreadedBinaryTree threadedBinaryTree = new ThreadedBinaryTree();
threadedBinaryTree.setRoot(root);
threadedBinaryTree.threadedNodes();
// 测试:以10号节点测试
HeroNode leftNode = node5.getLeft();
HeroNode rightNode = node5.getRight();
System.out.println("10号节点的前驱结点是:" + leftNode);// 3
System.out.println("10号节点的后继节点是:" + rightNode);// 1
// 当线索化二叉树后,不能再使用原来的遍历方法
// threadedBinaryTree.midOrder();
System.out.println("使用线索化的方式,遍历线索化二叉树~");
threadedBinaryTree.threadedList();
}
}
//定义ThreadedBinaryTree 实现了线索化功能的二叉树
class ThreadedBinaryTree {
private HeroNode root;
//为了实现线索化,需要创建要给指向当前节点的前驱节点的指针
//在递归进行线索化时,pre 总是保留前一个节点
private HeroNode pre = null;
public void setRoot(HeroNode root) {
this.root = root;
}
// 遍历线索化二叉树的方法
public void threadedList() {
// 定义一个变量,存储当前遍历的节点,从root开始
HeroNode node = root;
while (node != null) {
// 循环找到leftType == 1的节点,第一个找到的就是8节点
// 后面随着遍历而变化,因为当leftType == 1时,说明该节点是
// 按照线索化处理后的有效节点
while (node.getLeftType() == 0) {
node = node.getLeft();
}
// 打印当前节点
System.out.println(node);
// 如果当前节点的右指针指向的是后继节点,就一直输出
while (node.getRightType() == 1) {
// 获取到当前节点的后继节点
node = node.getRight();
System.out.println(node);
}
// 替换这个遍历的节点
node = node.getRight();
}
}
// 重载threadedNodes方法
public void threadedNodes() {
this.threadedNodes(root);
}
// 编写对二叉树进行中序线索化的方法
/**
* @param node 就是当前需要线索化的节点
*/
public void threadedNodes(HeroNode node) {
// 如果node == null,不能线索化
if (node == null) {
return;
}
// (一)先线索化左子树
threadedNodes(node.getLeft());
// (二)线索化当前节点【有难度】
// 处理当前节点的前驱节点
// 以8节点来理解
// 8节点.left = null, 8节点.leftType = 1;
if (node.getLeft() == null) {
// 让当前节点的左指针指向前驱节点
node.setLeft(pre);
// 修改当前节点的左指针的类型,指向前驱节点
node.setLeftType(1);
}
// 因为是单向的,所以不能同时处理左右,后继节点就放在后面处理
// 处理后继节点
if (pre != null && pre.getRight() == null) {
// 让前驱节点的右指针,指向当前节点
pre.setRight(node);
// 修改前驱节点的右指针类型
pre.setRightType(1);
}
// !!!!!!每处理一个节点后,就让当前节点是下一个节点的前驱节点
pre = node;
// (三)再线索化右子树
threadedNodes(node.getRight());
}
// 删除结点
public void delNode(int no) {
if (root != null) {
// 如果只有一个root结点,这里立即判断root是不是要删除的结点
if (root.getNo() == no) {
root = null;
} else {
// 递归删除
root.delNode(no);
}
} else {
System.out.println("空树,不能删除~");
}
}
// 前序遍历
public void preOrder() {
if (this.root != null) {
this.root.preOrder();// 谁调用,this就指向谁,第一次调用时this就指向root
} else {
System.out.println("二叉树为空,无法遍历~");
}
}
// 中序遍历
public void midOrder() {
if (this.root != null) {
this.root.midOrder();
} else {
System.out.println("二叉树为空,无法遍历~");
}
}
// 后序遍历
public void postOrder() {
if (this.root != null) {
this.root.postOrder();
} else {
System.out.println("二叉树为空,无法遍历~");
}
}
// 前序遍历查找
public HeroNode preOrderSearch(int no) {
if (root != null) {
// 至少有一个结点
return root.preOrderSearch(no);
} else {
return null;
}
}
// 中序遍历查找
public HeroNode midOrderSearch(int no) {
if (root != null) {
return root.midOrderSearch(no);
} else {
return null;
}
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
if (root != null) {
return root.postOrderSearch(no);
} else {
return null;
}
}
}
//创建HeroNode
class HeroNode {
private int no;
private String name;
private HeroNode left;// 默认null
private HeroNode right;// 默认null
// 说明:
// 1、如果leftType == 0,表示指向的是左子树,如果1表示指向前驱节点
// 2、如果rightType == 0,表示指向的是右子树,如果1表示指向后继节点
private int leftType;
private int rightType;
public int getLeftType() {
return leftType;
}
public void setLeftType(int leftType) {
this.leftType = leftType;
}
public int getRightType() {
return rightType;
}
public void setRightType(int rightType) {
this.rightType = rightType;
}
public HeroNode(int no, String name) {
super();
this.no = no;
this.name = name;
}
public int getNo() {
return no;
}
public void setNo(int no) {
this.no = no;
}
public String getName() {
return name;
}
public void setName(String name) {
this.name = name;
}
public HeroNode getLeft() {
return left;
}
public void setLeft(HeroNode left) {
this.left = left;
}
public HeroNode getRight() {
return right;
}
public void setRight(HeroNode right) {
this.right = right;
}
@Override
public String toString() {
return "HeroNode [no=" + no + ", name=" + name + "]";
}
// 递归删除节点
// 1.如果删除的结点是叶子节点,则删除该节点
// 2.如果删除的结点是非叶子结点,则删除该子树
public void delNode(int no) {
// 思路
/**
* 1,因为我们的二叉树是单向的,所以我们是判断当前结点的子结点是否需要删除,而不能去判断当前这个结点是不是需要删除的
* 2.如果当前结点的左子结点不为空,并且左子结点就是要删除结点,就将this.left=null;并且就返回(结束递归删除)
* 3.如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this. right=null;并且就返回(结束递归删除)
* 4.如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除 5.如果第4步也没有删除结点,则应当向右子树进行递归删除
*/
// 2.如果当前结点的左子结点不为空,并且左子结点就是要删除结点,就将this.left=null;并且就返回(结束递归删除)
if (this.left != null && this.left.no == no) {
this.left = null;
return;
}
// 3.如果当前结点的右子结点不为空,并且右子结点就是要删除结点,就将this. right=null;并且就返回(结束递归删除)
if (this.right != null && this.right.no == no) {
this.right = null;
return;
}
// 4.如果第2和第3步没有删除结点,那么我们就需要向左子树进行递归删除
if (this.left != null) {
this.left.delNode(no);
// 这里先不要写return 防止左子树没有删除成功,需要进入右子树的递归删除
}
// 5.如果第4步也没有删除结点,则应当向右子树进行递归删除
if (this.right != null) {
this.right.delNode(no);
}
}
// 编写前序遍历的方法
public void preOrder() {
System.out.println(this);// 先输出父节点
// 递归向左子树前序遍历
if (this.left != null) {
this.left.preOrder();
}
// 递归向右子树前序遍历
if (this.right != null) {
this.right.preOrder();
}
}
// 中序遍历
public void midOrder() {
if (this.left != null) {
this.left.midOrder();
}
System.out.println(this);// 再输出父节点
// 递归向右子树中序遍历
if (this.right != null) {
this.right.midOrder();
}
}
// 后序遍历
public void postOrder() {
if (this.left != null) {
this.left.postOrder();
}
// 递归向右子树后序遍历
if (this.right != null) {
this.right.postOrder();
}
System.out.println(this);// 最后输出父节点
}
// 前序遍历查找
/**
* @param no 查找no
* @return 找到就返回该Node,否则返回null
*/
public HeroNode preOrderSearch(int no) {
System.out.println("进入前序查找~");
// 比较当前结点是不是
if (this.no == no) {
return this;
}
// 1.判断当前结点的左子节点是否为空,若不为空,则递归前序查找
// 2.如果左递归前序查找,找到结点,则返回
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.preOrderSearch(no);
}
if (resNode != null) {
// 说明我们左子树找到
return resNode;
}
// 1.左递归前序查找,找到结点,则返回,否则继续判断,
// 2.当前结点的右子节点是否为空,如果不为空,则继续向右递归前序查找。
if (this.right != null) {
resNode = this.right.preOrderSearch(no);
}
return resNode;
}
// 中序遍历查找
public HeroNode midOrderSearch(int no) {
// 判断当前结点的左子节点是否为空,如果不为空,则递归中序查找。
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.midOrderSearch(no);
}
if (resNode != null) {
return resNode;
}
System.out.println("进入中序查找~");
// 如果找到,则返回,如果没找到,就和当前结点比较,如果是则返回当前结点
if (this.no == no) {
return this;
}
// 否则,向右进行右递归的中序查找
if (this.right != null) {
resNode = this.right.midOrderSearch(no);
}
return resNode;
}
// 后序遍历查找
public HeroNode postOrderSearch(int no) {
// 判断当前节点的左子节点是否为空,如果不为空,则递归后序查找
HeroNode resNode = null;
if (this.left != null) {
resNode = this.left.postOrderSearch(no);
}
if (resNode != null) {
// 说明在左子树找到
return resNode;
}
// 如果左子树没有找到,就向右子树递归进行后序遍历查找
if (this.right != null) {
resNode = this.right.postOrderSearch(no);
}
if (resNode != null) {
// 说明在右子树找到
return resNode;
}
System.out.println("进入后序查找~");
// 如果左右子树都没有找到,就比较当前结点是不是
if (this.no == no) {
return this;
}
return resNode;
}
}