1、钞票找零
A听说朋友新开了一个柠檬水摊,每一杯柠檬水的售价为 5 元。
顾客排队购买产品,(按账单 bills 支付的顺序)一次购买一杯。
每位顾客只买一杯柠檬水,然后向老板付 5 元、10 元或 20 元。老板必须给每个顾客正确找零,也就是说净交易是每位顾客向老板支付 5 元。
但是因为是第一次做生意,一开始老板手头没有任何零钱,这就导致可能无法给顾客找零,得到差评。Alan的朋友想请你编写程序,判断按照账单是否能正确找零。
输入格式:
给定一个账单bills,列表形式。
输出格式:
如果你能给每位顾客正确找零,返回 True ,否则返回 False 。
输入样例:
[5,5,5,10,20]
输出样例:
True
样例说明:
- 前 2 位顾客那里,我们按顺序收取 2 张 5 元的钞票。
- 对于接下来的 2 位顾客,我们收取一张 10 元的钞票,然后返还 5 元。
- 对于最后一位顾客,我们无法退回 15 元,因为我们现在只有两张 10 元的钞票。
- 由于不是每位顾客都得到了正确的找零,所以答案是 False。
要点:只需要判断列表里的元素即可,但是要注意将每一种情况都要考虑在内
def change(bills):
if bills[0]!=5:
return False
else:
bills2 = bills[1:]
five_money=1
ten_money=0
for i in bills2:
if i == 5: # 有支付 5元的
five_money += 1
elif i == 10: # 有支付10元的
five_money -= 1
ten_money += 1
else: # 有支付20元的
if ten_money >= 1:
ten_money -= 1
five_money -= 1
else:
five_money -= 3
if five_money < 0 or ten_money < 0: #看看是否是把5元的和10元的给减没了
return False
return True
if __name__=='__main__':
bills = list(map(int,eval(input())))
# bills = eval(input())
#print(bills)
canchange = change(bills)
if canchange==False:
print('False',end="")
else:
print("True",end="")
# a = list(map(int,eval(input())))
# print(a)
2、串珠子
A 恰巧碰到kekao师傅在串手链。哦,原来是kekao师傅觉得买的手链没有自己做的更有心意,于是他买了一堆珠子准备自己做一个,但他是一个重度选择困难症患者,于是Alan提议,至少保证手链一半以上的位置有珠子。但是Alan和kekao不知道有多少种串法,想请你帮忙计算一下。对于一个长度为n的绳子来说,每一个位置可以放上一个珠子,有珠子表示为1,没珠子表示为0。
输入格式:
输入一个正整数n (1≤n≤18)
输出格式:
输出每一个串,每个串占一行 (从小到大输出)串的长度是n。
最后一行输出串法的数量。
输入样例:
3
输出样例:
011
101
110
111
amount = 4
样例说明:
对于长度为3的串,所有串法是:
000
001
010
011
100
101
110
111
但是要保证每一个手链的珠子数量大于串长度的一半,于是得到上述答案。
要点:
通过题意我们可以知道对于长度为n的绳子,01串的串法数量是2^ n。而我们需要将其排序组合,不难发现对于长度为n,数值最小的串是n个0,最大的是n个1,这与二进制非常相似。事实证明,对于长度为n的01串,如果我们将其看成二进制,那么它转化为十进制的数值范围是0 ~ 2^ n -1。所以问题就转化为求0~ 2^ n-1的二进制,并判断01串中0与1的数量即可。但是我们知道2^n存在指数爆炸,所以要考虑时间问题,此处我们采用按位与运算,而不是内置bin()函数,可以大幅降低时间。
n = int(input())
amo = 0
def f(r):
global amo
st = ""
while(r):
# print(r&1,end=" ")
st += str((r & 1))
r >>= 1
while(len(st) < n):
st += "0"
if st.count("1") > len(st)/2:
print(st[::-1])
amo += 1
temp = 2**n
for i in range(0,temp):
f(i)
print("amount = {}".format(amo))
3、跳楼梯
为了锻炼,A 一次只跳1阶楼梯,或者一次跳上2阶楼梯。问Alan要上一个n阶的楼梯,最多有多少种不同上楼的走法?
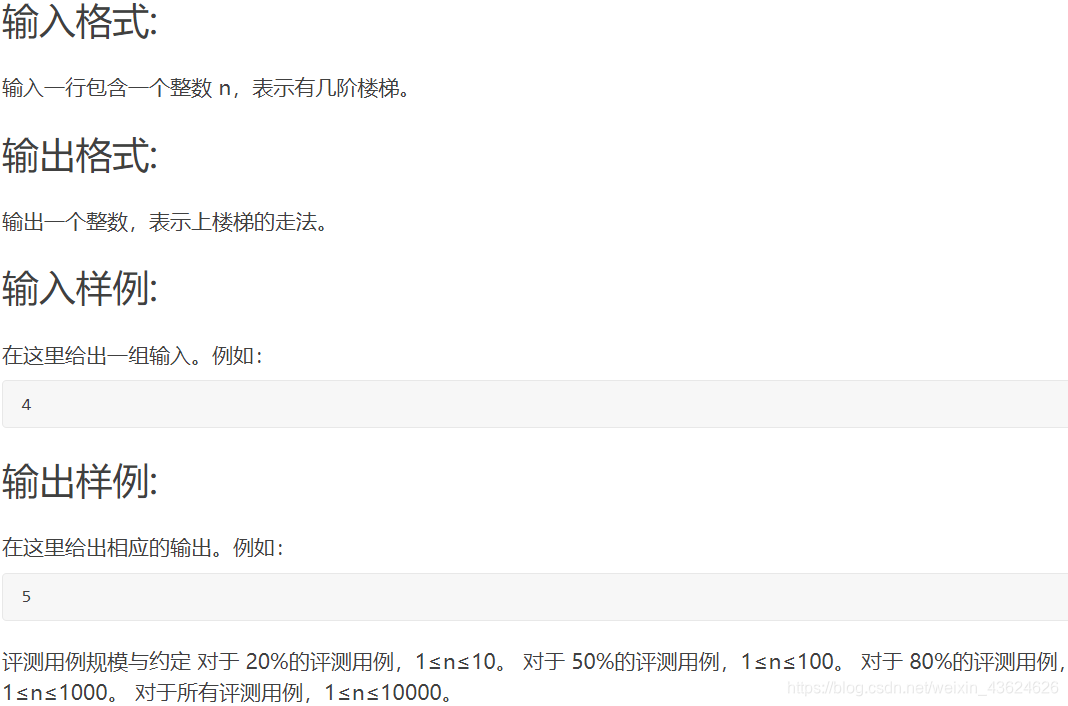
要点:设结果为 x
- 当n = 1的时候,x = 1
- 当n = 2的时候,x = 2
- 当n = 3的时候,x = 3
- 当n = 4的时候,x = 5
这个过程与斐波那契数列是一致的,但是需要注意这里是 1,2,3,5 不是
1,1,2,3,5
那么只要将n的值往上加1 n = n+1 ,此时结果与斐波那契数列一致。
res = []
n = int(input())
res.append(1)
res.append(2)
for i in range(2,n):
res.append(res[i-1] + res[i-2])
print(res[n-1])
4、素数对
将1……N的数字按照升序排列,在下一行按照降序排列。
1 2 3 … … N-1 N
N N-1 N-2 … … 2 1
按照上述排列,对于给定的n,有多少个素数对?
输入格式:
在一行中给定一个整数N (1≤N≤10^4)
输出格式:
输出一个整数表示素数对的个数
输入样例:
3
输出样例:
1
样例说明:
1 2 3
3 2 1
素数对是:
| 2 |
| 2 |
要点:对于上一列的第i个,在下一列与其成对的存在是 n+1-i。
def prime(num):
if num == 1:
return 0
elif num == 2:
return 1
else:
for i in range(2,int(num**0.5)+1):
if num%i == 0:
return 0
return 1
n = int(input())
res = 0
if n < 2:
res = 0
else:
for i in range(2,n+1):
if prime(i) and prime(n+1-i):
res += 1
print(res)
5、不同进制的A+B
求两个数的和。
但是输入的数字可能是二进制,八进制,十进制,十六进制,输出的和要求是二进制。
输入格式:
输入分为两行,每一行包含两个字符串,第一个字符串代表进制,第二个字符串代表数字。
b或B代表二进制,o或O代表八进制,d或D代表十进制,x或X代表十六进制。
输出格式:
在一行中输出两个数的和的二进制,不包含前导0
输入样例1:
o 7
d 9
输出样例1:
10000
输入样例2:
B 11
x ab
输出样例2:
10101110
要点:
- 本题主要是熟悉各进制数字间的运算,可以将其都转化为我们熟悉的十进制运算,再输出二进制结果。
- Python 内置函数进制转换的用法(十进制转二进制、八进制、十六进制)
bsys_a,num_a = input().split()
bsys_b,num_b = input().split()
if bsys_a in ("b","B"):
add_a = int(num_a,2)
if bsys_a in ("o","O"):
add_a = int(num_a,8)
if bsys_a in ("d","D"):
add_a = int(num_a)
if bsys_a in ("x","X"):
add_a = int(num_a,16)
if bsys_b in ("b","B"):
add_b = int(num_b,2)
if bsys_b in ("o","O"):
add_b = int(num_b,8)
if bsys_b in ("d","D"):
add_b = int(num_b)
if bsys_b in ("x","X"):
add_b = int(num_b,16)
x = add_a + add_b
print(bin(x).replace("0b","")) # bin()返回值为字符转