一、瞻仰先人:贝叶斯介绍:

贝叶斯(约1701-1761) Thomas Bayes,英国数学家。约1701年出生于伦敦,做过神甫。1742年成为英国皇家学会会员。1761年4月7日逝世。贝叶斯在数学方面主要研究概率论。他首先将归纳推理法用于概率论基础理论,并创立了贝叶斯统计理论,对于统计决策函数、统计推断、统计的估算等做出了贡献。他死后,理查德·普莱斯 (Richard Price)于1763年将他的著作《机会问题的解法》(An essay towards solving a problem in the doctrine of chances)寄给了英国皇家学会,对于现代概率论和数理统计产生了重要的影响。
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
二、贝叶斯公式介绍:
2.1、公式定义:
设 A 1 , A 2 , . . . , A n A_1,A_2,...,A_n A1,A2,...,An为一个完备事件组,其中 P ( A ) > 0 , i = 1 , 2 , . . . , n P(A)>0,i=1,2,...,n P(A)>0,i=1,2,...,n。则对于任意事件B,如果 P ( B ) > 0 P(B)>0 P(B)>0,则有:
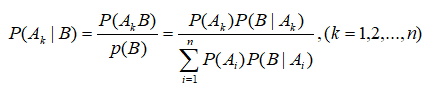
- 上公式前半段解释:在B事件发生的概率下, A k A_k Ak事件发生的概率= A k A_k Ak、B事件发生的联合概率/B事件发生的概率;
- 上公式前半段除式变乘式,贝叶斯公式也即:P(AB)=P(A|B)P(B)=P(B|A)P(A);用Venn图表示即为下左图:
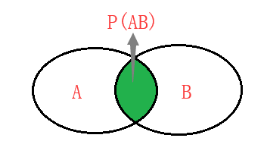
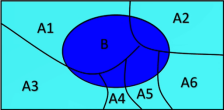
- 上公式前半段的分母P(B)用全概率公式展开为: P ( B ) = P(B)= P(B)= ∑ \sum ∑ P ( A i ) P ( B ∣ A i ) P(A_i)P(B|A_i) P(Ai)P(B∣Ai),全概率公式可参见上右图;
- 结合上面的2、3步,即可得到贝叶斯公式的后半段;
- 我们常把 P ( A k ∣ B ) P(A_k|B) P(Ak∣B)称为后验概率, P ( A k ) P(A_k) P(Ak)称为先验概率, P ( B ∣ A k ) P(B|A_k) P(B∣Ak)称为似然函数。【似然函数解释:给定输出x时,关于参数θ的似然函数L(θ|x),在数值上等于给定参数θ后变量X的概率:L(θ|x)=P(X=x|θ)】——所以贝叶斯公式也说明:后验概率是可以通过先验概率和似然函数计算出来的。这就是贝叶斯流派认同的观点;
–-----------------------------------------------------------------------------—----------------------------------------
2.2、出个小题:
已知一所学校里男生占60%,女生占40%,男生总是穿长裤,女生则一半穿长裤一半穿裙子。问:你在校园里随机遇到一个穿长裤的人,Ta是男生的概率是多少?
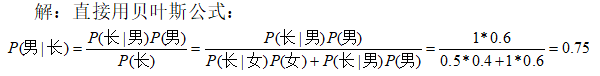
–-----------------------------------------------------------------------------—------------------------------------–
–-----------------------------------------------------------------------------—------------------------------------–
–-----------------------------------------------------------------------------—------------------------------------–
三、朴素贝叶斯算法原理:
3.1、朴素贝叶斯算法简介:(重点)
在分类问题中,我们常常需要根据新样本所具有的属性将其划分到某个类别中;
- 我们有一个训练集,也叫样本空间 C = X 1 , X 2 , . . . , X n C=X_1,X_2,...,X_n C=X1,X2,...,Xn;
- 当一个样本 X X X具有多条属性时,把它的众多属性看做是一个向量,即样本 X = ( x 1 , x 2 , . . . , x n ) X=(x_1,x_2,...,x_n) X=(x1,x2,...,xn);(这里 X X X是样本, x i x_i xi是样本具有的属性,组成样本空间);
- 样本空间具有的所有类别标签: Y = ( y 1 , y 2 , . . . , y m ) Y=(y_1,y_2,...,y_m) Y=(y1,y2,...,ym);样本空间每一条样本 X X X都对应一个类别标签 y y y;
- 计算新样本 X 0 X_0 X0属于每一个类别标签的概率: P ( y 1 ∣ X 0 ) , P ( y 2 ∣ X 0 ) , . . . , P ( y m ∣ X 0 ) P(y_1|X_0),P(y_2|X_0),...,P(y_m|X_0) P(y1∣X0),P(y2∣X0),...,P(ym∣X0);
- 如果 P ( y k ∣ X 0 ) = m a x ( P ( y 1 ∣ X 0 ) , P ( y 2 ∣ X 0 ) , . . . , P ( y m ∣ X 0 ) ) P(y_k|X_0)=max(P(y_1|X_0),P(y_2|X_0),...,P(y_m|X_0)) P(yk∣X0)=max(P(y1∣X0),P(y2∣X0),...,P(ym∣X0)),就把新样本 X 0 X_0 X0划分到 y k y_k yk类。(将概率最大的类别标签 y k y_k yk作为新样本 X X X的标签);
–-----------------------------------------------------------------------------—----------------------------------------
3.2、如何计算 P ( y k ∣ X ) P(y_k|X) P(yk∣X)
从上面3.1的简介里可以看出,最重要的一步就是第4步,那么如何计算 P ( y k ∣ X ) P(y_k|X) P(yk∣X)就是这里研究的重点:

说明:上式的计算方法是假设在 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn相互独立的基础上,而在工业运用上 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn大多不是完全相互独立的,所以上式应该为约等于。而如果 x 1 , x 2 , . . . , x n x_1,x_2,...,x_n x1,x2,...,xn的相关性很强,也就是 x k , x l x_k,x_l xk,xl可能相互影响时,就建议不要用朴素贝叶斯的方法,得到的效果会很差。
–-----------------------------------------------------------------------------—----------------------------------------
3.3、举例
有下面这个相亲数据表,问:当有一个具有(矮、富、帅)的新样本出现,是见还是不见?
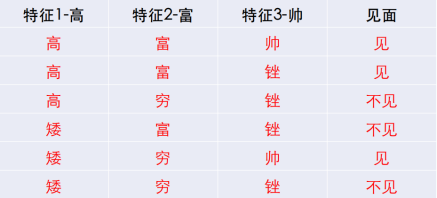
- 分析:其实就是用朴素贝叶斯求 m a x ( P ( 见 ∣ [ 矮 、 富 、 帅 ] ) , P ( 不 见 ∣ [ 矮 、 富 、 帅 ] ) ) max(P(见|[矮、富、帅]),P(不见|[矮、富、帅])) max(P(见∣[矮、富、帅]),P(不见∣[矮、富、帅])),
以下是 P ( 见 ∣ [ 矮 、 富 、 帅 ] ) P(见|[矮、富、帅]) P(见∣[矮、富、帅])的计算过程,有兴趣的伙伴自己计算 P ( 不 见 ∣ [ 矮 、 富 、 帅 ] ) P(不见|[矮、富、帅]) P(不见∣[矮、富、帅])

举例说明 P ( 矮 ∣ 见 ) = P(矮|见)= P(矮∣见)= 1 3 1 \over 3 31的计算过程:
在上面数据集中,“见”总共有3条数据,在这3条数据中,“矮”出现了1次,所以 P ( 矮 ∣ 见 ) = P(矮|见)= P(矮∣见)= 1 3 1 \over 3 31
–-----------------------------------------------------------------------------—----------------------------------------
3.4、拉普拉斯修正:
如果数据集变成如下,还是(矮、富、帅)这个样本出现,是见还是不见?

分析:还是用朴素贝叶斯求 m a x ( P ( 见 ∣ [ 矮 、 富 、 帅 ] ) , P ( 不 见 ∣ [ 矮 、 富 、 帅 ] ) ) max(P(见|[矮、富、帅]),P(不见|[矮、富、帅])) max(P(见∣[矮、富、帅]),P(不见∣[矮、富、帅])),但是出现了问题:
由于 P ( 矮 ∣ 见 ) = P(矮|见)= P(矮∣见)= 0 2 0 \over 2 20 = 0 =0 =0,那么计算出来的 P ( 见 ∣ [ 矮 、 富 、 帅 ] ) P(见|[矮、富、帅]) P(见∣[矮、富、帅])也是等于0。数据集的特例,对我们的计算结果产生了影响,为了规避这个情况,我们就需要引入拉普拉斯修正的方法:
拉普拉斯修正公式:分子+1,分母+k
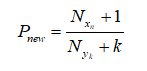
解释:
- k :是样本空间具有的所有类别标签的总个数;
- 分子:是标签= y k y_k yk且样本属性= x n x_n xn样本的个数;
- 分母:是标签= y k y_k yk的样本个数;
结合上面,就是把 P ( 矮 ∣ 见 ) = P(矮|见)= P(矮∣见)= 0 2 0 \over 2 20的分子+1,分母+k;
由于样本空间的类别标签 Y = ( 见 , 不 见 ) Y=(见,不见) Y=(见,不见),所以 k = 2 k=2 k=2,
经过拉普拉斯修正后: P ( 矮 ∣ 见 ) = P(矮|见)= P(矮∣见)= 0 + 1 2 + 2 0+1 \over 2+2 2+20+1, P ( 富 ∣ 见 ) = P(富|见)= P(富∣见)= 2 + 1 2 + 2 2+1 \over 2+2 2+22+1, P ( 帅 ∣ 见 ) = P(帅|见)= P(帅∣见)= 1 + 1 2 + 2 1+1 \over 2+2 2+21+1,所以
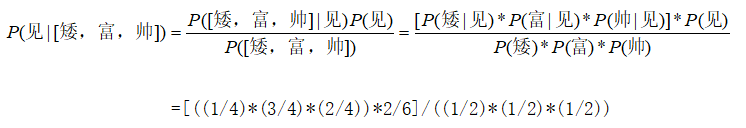
有兴趣的伙伴自己计算 P ( 不 见 ∣ [ 矮 、 富 、 帅 ] ) ) P(不见|[矮、富、帅])) P(不见∣[矮、富、帅])),记得要使用拉普拉斯修正;
计算后比较“见”与“不见”两个数值,哪个大就选择哪个;
这以上就是朴素贝叶斯算法所有的内容。
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
四、高斯贝叶斯算法:
以上的例子用到的数据都是离散化的数据,但如果遇到下面连续数值怎么处理呢?
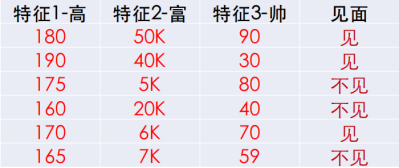
我们需要将连续的数值转化为离散的数据,以下介绍两种方法:
–-----------------------------------------------------------------------------—----------------------------------------
4.1、分箱法:
将连续数据分段形成离散数据的预处理方法。以170分出高矮、20K分出富穷、60分出帅丑,得到离散数据如下:
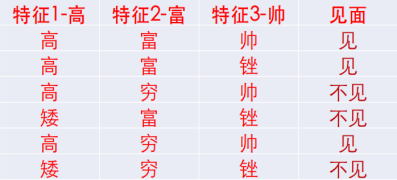
出现问题:分箱法更多依赖于经验,按照上面的分箱法,170与190都被分作“高”,显然差距有点大,有没有什么方法能更好的保持原有数据的特征,又能表达概率的呢!
–-----------------------------------------------------------------------------—----------------------------------------
4.2、高斯分布(正态分布):
我们只需计算各类特征下的均值和方差:

比如:有以下样本空间,问(170,30k,70)是见还是不见?
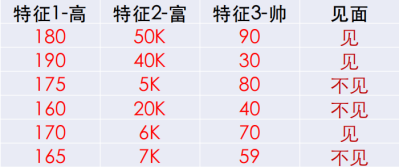
分析:还是计算 m a x ( P ( 见 ∣ [ 170 , 30 k , 70 ] ) , P ( 不 见 ∣ [ 170 , 30 k , 70 ] ) ) max(P(见|[170,30k,70]),P(不见|[170,30k,70])) max(P(见∣[170,30k,70]),P(不见∣[170,30k,70]))
解:求 P ( 见 ∣ [ 170 , 30 k , 70 ] ) P(见|[170,30k,70]) P(见∣[170,30k,70])
P ( 见 ∣ [ 170 , 30 k , 70 ] ) = [ ( P ( 170 ∣ 见 ) ∗ P ( 30 K ∣ 见 ) ∗ P ( 70 ∣ 见 ) ) ∗ P ( 见 ) ] / [ P ( 170 ) ∗ P ( 30 k ) ∗ P ( 70 ) ] P(见|[170,30k,70])=[(P(170|见)*P(30K|见)* P(70|见))*P(见)]/[P(170)* P(30k)* P(70)] P(见∣[170,30k,70])=[(P(170∣见)∗P(30K∣见)∗P(70∣见))∗P(见)]/[P(170)∗P(30k)∗P(70)]
以特征1-身高为例:
若“身高”的均值为180,标准差为8.24,则 P ( 170 ∣ 见 ) P(170|见) P(170∣见)的概率为:

剩下的以特征2-财富值、特征3-颜值的计算过程也是带入上公式。
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
–-----------------------------------------------------------------------------—----------------------------------------
结束语:
- 朴素贝叶斯算法原理就到这里。除去高斯贝叶斯外,还有多项式贝叶斯、伯努利贝叶斯,有兴趣的同学自己研究。博主也会在以后继续更新。
- 代码在sklearn都有范例,也比较简单。
- 下一篇博客是《【机器学习】10:朴素贝叶斯做酒店评论分类》,是这篇博客的实战,有兴趣的伙伴继续交流。