贪心的本质
选择每一阶段的局部最优,从而达到全局最优


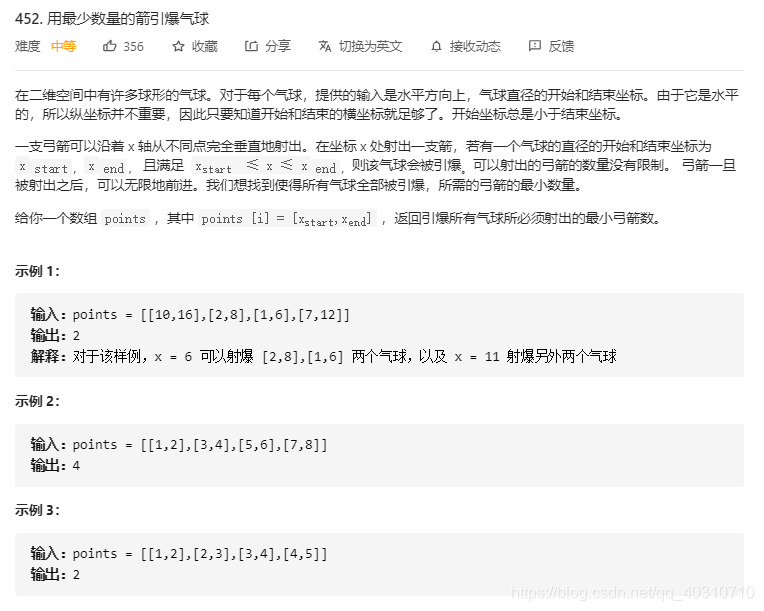
思路
将小孩按照胃口从小到大排序,因为要满足的数量最多,所以从胃口小的开始满足(贪心)
将饼干的大小从小到大排序。
当饼干小于当前孩子的胃口时,说明这个饼干不能满足剩下的所有孩子,所以选择下一块饼干(j++)
当第一次找到饼干大于孩子胃口时,将这块饼干给孩子(count++)
再次更新孩子以及饼干,重复操作
class Solution {
public int findContentChildren(int[] g, int[] s) {
Arrays.sort(g);
Arrays.sort(s);
int numsofchildren = g.length;
int numsofcookies = s.length;
int count = 0;
for(int i=0,j=0; i<numsofchildren&&j<numsofcookies; i++,j++){
while(j<numsofcookies && g[i]>s[j]){
注意这个while直到我们找到能满足当前小孩的饼干并发给他,我们才进行下一次for循环
j++;
}
if(j<numsofcookies){
count++;
}
}
return count;
}
}
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
if (n < 2) {
return n;
}
int prevdiff = nums[1] - nums[0];
int ret = prevdiff != 0 ? 2 : 1;
for (int i = 2; i < n; i++) {
int diff = nums[i] - nums[i - 1];
if ((diff > 0 && prevdiff <= 0) || (diff < 0 && prevdiff >= 0)) {
ret++;
prevdiff = diff;
}
}
return ret;
}
}
class Solution {
public int wiggleMaxLength(int[] nums) {
int n = nums.length;
// 1. 长度为1的都是摆动序列
if(n < 2){
return n;
}
// 2. 初始化
int prevdiff = nums[1] - nums[0]; // 记录相邻三个元素 x y z(x 和 y 的差是正还是负)
int ret = prevdiff != 0?2:1; // 前两个元素是否有重复 前面元素重复时ret=1表示只能构成摇摆序列的一个元素
// 3. 贪心遍历数组:加入一个新元素
for(int i = 2;i < n;i++){
int diff = nums[i] - nums[i - 1]; // 记录相邻三个元素 x y z(y 和 z 的差是正还是负)
if((diff > 0 && prevdiff <= 0) || (diff < 0 && prevdiff >= 0)){
// 判断当前序列的上升下降趋势
ret++; // 如果出现了「峰」或「谷」,答案加一
prevdiff = diff; // 更新当前序列的上升下降趋势
}
}
return ret; // 返回结果
}
}

class Solution {
public int maxSubArray(int[] nums) {
int ans = nums[0];
int sum = 0;
for(int num:nums){
if(sum>0){
sum += num;
}
else{
sum = num;
}
ans = Math.max(ans,sum);
}
return ans;
}
}

动态规划解决的该问题,也可以用贪心的方法解决
动态规划,dp[][0]对应的是当天不持股的收益,不持股的收益包括max(昨天持股+今天的价格,以及昨天不持股的收益,今天仍然不买入)
dp[][1]当天持股收益,包括max(昨天持股今天不卖 以及昨天不持股今天买入的收益)
class Solution {
public int maxProfit(int[] prices) {
int n = prices.length;
int[][] dp = new int[n][2];
dp[0][0] = 0;
dp[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1] + prices[i]);
dp[i][1] = Math.max(dp[i - 1][1], dp[i - 1][0] - prices[i]);
}
return dp[n - 1][0];
}
}
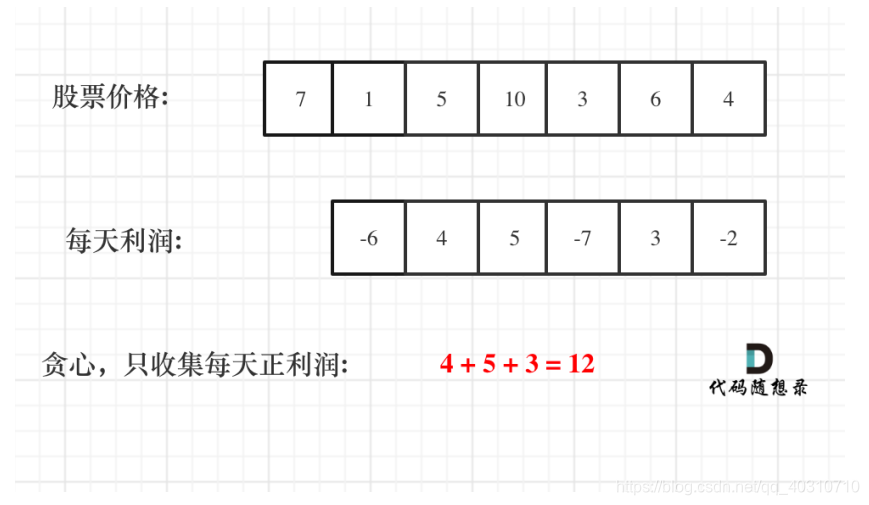
贪心解决:
局部最优:收集每天的正利润
全局最优:取得最大利润
计算相邻两天的差值,找到正的

public class Solution {
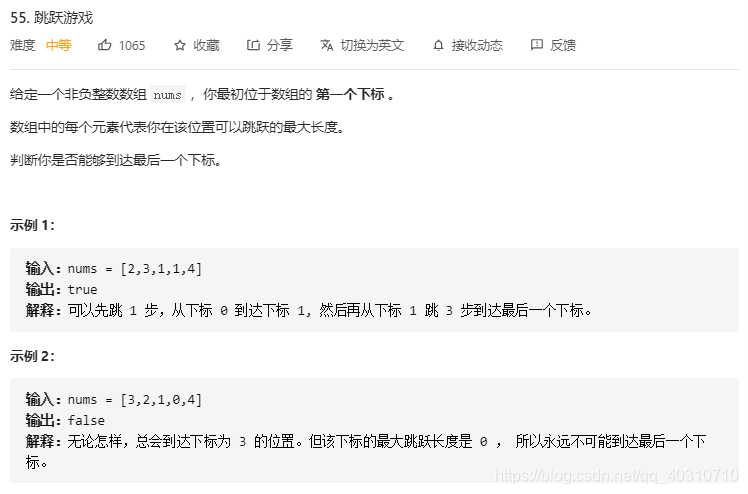
public boolean canJump(int[] nums) {
int n = nums.length;
int rightmost = 0;
for (int i = 0; i < n; ++i) {
//从位置0开始,我们保存能够到达的最远位置,rightmost,当rightmost大于等于当前位置时,说明该位置我们能够达到,我们能达到的最远距离包括,上一次循环保存的最远距离以及当前位置+当前位置的最大跳跃距离 更新二者中的最大值作为rightmost
rightmost大于len-1则true
当i>rightmost时,说明我们不能达到该位置,所以flase
if (i <= rightmost) {
rightmost = Math.max(rightmost, i + nums[i]);
if (rightmost >= n - 1) {
return true;
}
}
}
return false;
}
}
public class Solution {
public boolean canJump(int[] nums) {
int n = nums.length;
int rightmost = 0;
for (int i = 0; i < n; ++i) {
if(i>rightmost){
return false;
}
//if (i <= rightmost) {
rightmost = Math.max(rightmost, i + nums[i]);
if (rightmost >= n - 1) {
return true;
}
}
return false;
}
}
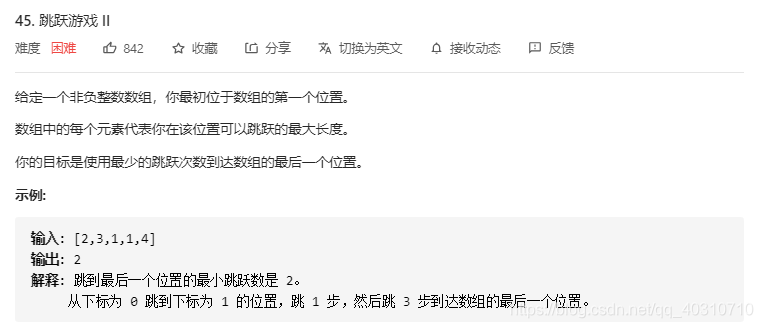
跳跃游戏2理解存在问题
class Solution {
public int jump(int[] nums) {
int position = nums.length - 1;
int steps = 0;
while (position > 0) {
for (int i = 0; i < position; i++) {
if (i + nums[i] >= position) {
只有在当前位置+当前能跳跃的最大值>=position时,step才+1
position = i;
steps++;
break;
}
}
}
return steps;
}
}
public int jump(int[] nums) {
int end = 0;
int maxPosition = 0;
int steps = 0;
for(int i = 0; i < nums.length - 1; i++){
//找能跳的最远的
maxPosition = Math.max(maxPosition, nums[i] + i);
if( i == end){
//遇到边界,就更新边界,并且步数加一
end = maxPosition;
steps++;
}
}
return steps;
}

先排序,如果第一个元素是 >= 0 则一直对第一个元素取反操作,否则,对< 0 的元素依次取反,直到所有的 < 0 的元素都完成取反操作之后,再次排序,再依次对 第一个 >= 0 的数 做剩余次数的取反
思路:有负数翻转负数,负数翻完了,反复翻转最小的整数
class Solution {
public int largestSumAfterKNegations(int[] A, int K) {
Arrays.sort(A);
int i=0;
int sum = 0;
int n = A.length;
while(A[i]<0 && K>0){
A[i] = -A[i];
i++;
K--;
}
Arrays.sort(A);
if(K%2==1){
A[0]=-A[0];
}
for(int a:A){
sum = sum+a;
}
return sum;
}
}