
paper:https://arxiv.org/abs/2101.0369
code:
文章目录
1. Motivation
如今更复杂的卷积网络可以取得更大的精度,但是相对于简单的卷积网络来说,也有2种缺点,首先是多分支结构中复杂的设定,以及复杂卷积网络的计算资源的开销。
同时,其他simple ConvNets的性能并不能比得过complicated ConvNets。
2. Contribution
本文的贡献如下:
-
本文提出了RepVGG,一种简单,实现速度与精度平衡的SOTA 网络结构。
-
本文提出了structural re-parameterization 结构化重参数来解耦训练多分支拓扑以及测试单分支plain结构。
-
本文显示了VGG在图像分类以及语义分割上的实用性,高效并且利于实现。
RepVGG有以下优点:
- RepVGG模型是一种VGG-like 结构,没有许多分支,每一层的输入就是上一层的输出。
- RepVGG模型的body部分只包含了3x3卷积以及ReLU。
- RepVGG模型具体的结构没有automatic search,manual refinement人为加工,compound scaling 混合比例等设定。
3. Building RepVGG via Structural Re-param
3.1 Simple is Fast, Memory-economical, Flexible
使用simple ConvNets的原因在于快速,省内存以及灵活。
- Fast
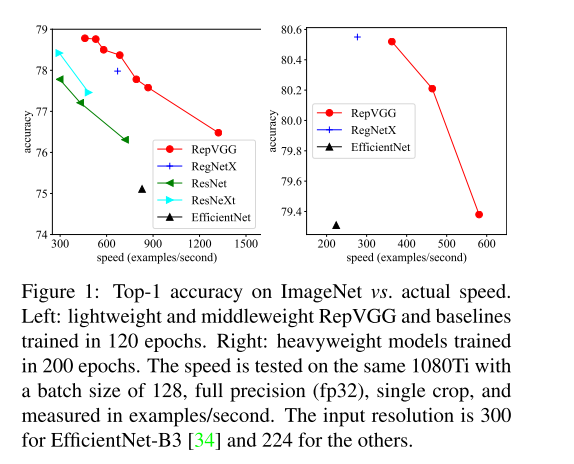
- Memory-economical
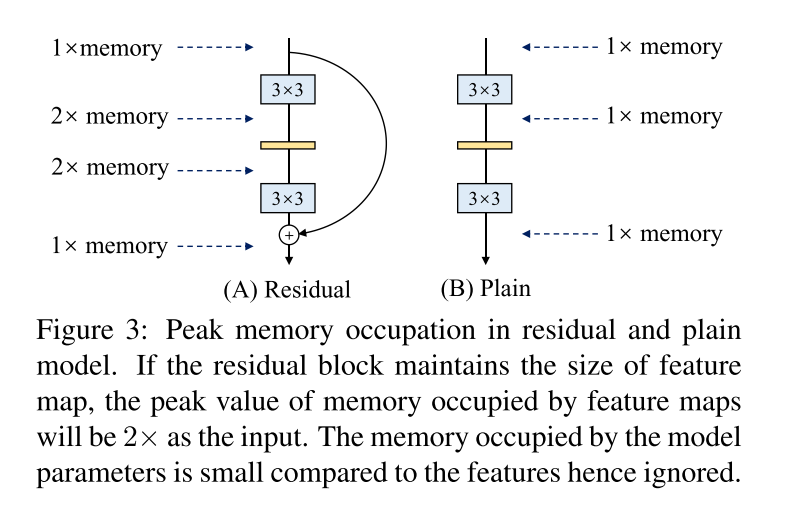
-
Flexible
多分支的拓扑结构暴露了网络结构上的局限性,例如输出的shape,res-block的最后一个卷积必须保持相同的shape,否则就无法实现short-cut;以及限制了channel purning通道剪枝的应用。
3.2 Traing-time Multi-branch Architecture
作者收到ResNet启发,并且通过相关的研究发现,ResNet之所以性能比VGG好的原因,ResNet的分支结构shortcut,可以使得模型具有一种大量子模型的隐式ensemble。确切来说,假如模型有n个blocks,模型可以被表示为 2 n 2^n 2n的ensemble模型(根据作者的解释,每遇到一次分支,总的路径救护变成2倍),单路架构显然不具备这种特点。
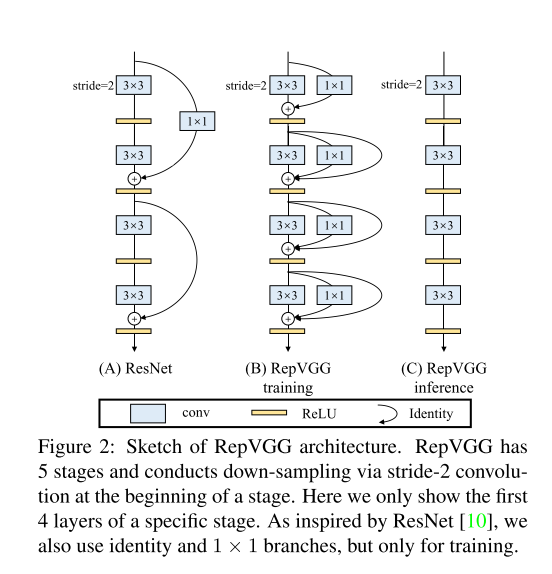
由于多分支拓扑在inference过程存在缺点,但又利于训练,因此作者构建了一种只使用多分支结构用于training-time的模型。这样就可以同时利用多分支模型训练时的优势(性能高)和单路模型推理时的好处(速度快、省内存),如图2所示。这里的关键显然在于这种多分支模型的构造形式和转换的方式(3.3小节叙述)。ResNet中的Res-Block的计算公式为:
y = x + f ( x ) i f ( x . s i z e ( ) ≠ f ( x ) . s i z e ( ) ) : y = g ( x ) + f ( x ) y= x +f(x)\\ if ( x.size() \not= f(x).size()):\\ y = g(x) + f(x) y=x+f(x)if(x.size()=f(x).size()):y=g(x)+f(x)
受到ResNet的启发,RepVGG设计为三分支的结构,本文的实现方式为:在训练时,为每一个3x3卷积层添加平行的1x1卷积分支和恒等映射分支,构成一个RepVGG Block。这种设计是借鉴ResNet的做法,区别在于ResNet是每隔两层或三层加一分支,而RepVGG是每层都加。公式如下:
y = x + g ( x ) + f ( x ) y= x+g(x)+f(x) y=x+g(x)+f(x)
在训练过程中, f ( x ) f(x) f(x)表示的是和ResNet一样的1x1的shortcut分支,而$g(x) = y , , ,g(x)$为恒等映射,不经过卷积核,因此模型就成为了 3 n 3^n 3n的ensemble模型。
3.3 Architectural Specification
由公式1~公式5,可以得到由多分支结构转换为单分支卷积结构。
多分支结构中,通过3个卷积核以及各自的bn层,得到最终的feature map M,由公式1表示:
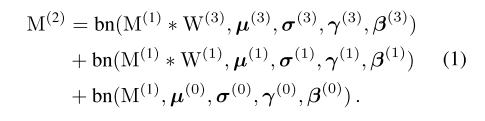
接着对于公式1中的每一项,由BN层的公式进行展开得到公式2:
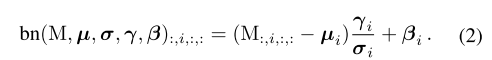
将公示2进行展开,得到新的 W i ′ W_i' Wi′和 b i ′ b_i' bi′:
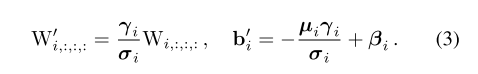
接着可以得到经过Conv以及BN层后的 y = W x + b y =Wx+b y=Wx+b的形式:
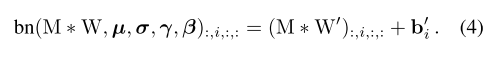
由于卷积的线性(可加性),假设三个3x3的卷积分别是W1,W2,W3,最终,有以下等式成立:
C o n v ( x , W 1 ) + B i a s 1 + C o n v ( x , W 2 ) + B i a s 2 C o n v ( x , W 3 ) + B i a s 3 = C o n v ( x , W 1 + W 2 + W + B i a s ) (5) Conv(x, W_1) +Bias_1+Conv(x, W_2) +Bias_2 Conv(x, W_3)+Bias_3=Conv(x, W_1+W_2+W+Bias) \tag{5} Conv(x,W1)+Bias1+Conv(x,W2)+Bias2Conv(x,W3)+Bias3=Conv(x,W1+W2+W+Bias)(5)
因此,可以对模型进行等价的转换,最后,三分支得到的卷积核和bias分别相加即可。这样,每个RepVGG Block转换前后的输出完全相同,因而训练好的模型可以等价转换为只有3x3卷积的单路模型, 将多分支模型等价转换为单路模型,得到部署的模型并且使用。
作者给出了一个非常例子以及图示,如图4所示,假设 C 1 = C 2 = 2 C_1 =C_2=2 C1=C2=2,那么对于 3 × 3 3 \times 3 3×3以及 1 × 1 1 \times 1 1×1的Kernel,它们的size分别为 3 × 3 × 2 × 2 3\times3\times2\times2 3×3×2×2以及 1 × 1 × 2 × 2 1\times1\times2\times2 1×1×2×2。也就是说,它们分别有 4 × 3 × 3 4\times 3 \times 3 4×3×3和 2 × 2 2 \times 2 2×2的卷积矩阵,对于identity本身来说,可以理解为是一种identity matrix的 1 × 1 1 \times 1 1×1的单位矩阵。对于每一个分支,都有BN层的4个参数 [ μ , σ , γ , β ] [\mu,\sigma,\gamma,\beta ] [μ,σ,γ,β]。
RepVGG Blcok转换为一个卷积的方式为: 1 × 1 1 \times 1 1×1的矩阵可以看成是只有中心位置是有参数其他位置的值都是0的 3 × 3 3\times3 3×3 卷积核;同样,恒等映射是一种以单位矩阵为卷积核的 1 x 1 1x1 1x1卷积,同时进一步的转换为 3 × 3 3\times 3 3×3 卷积。
An explanation for the success of ResNets is that such a multi-branch architecture makes the model an implicit ensemble of numerous shallower models
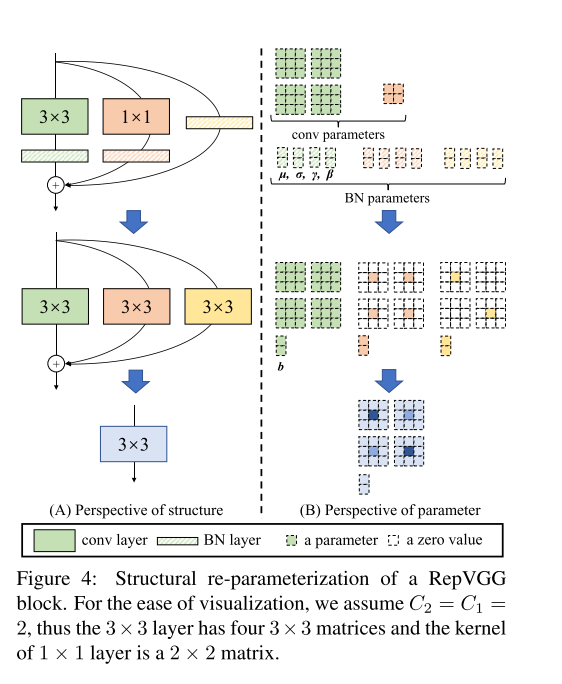
从这一转换过程中,我们看到了“结构重参数化”的实质:训练时的结构对应一组参数,推理时我们想要的结构对应另一组参数;只要能把前者的参数等价转换为后者,就可以将前者的结构等价转换为后者。
4.Experiments
4.1 RepVGG for ImageNet Classification
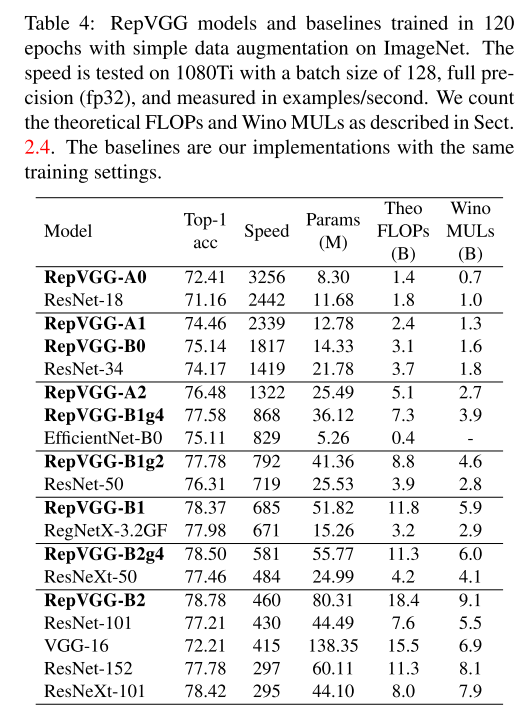
训练200个epochs的实验结果:
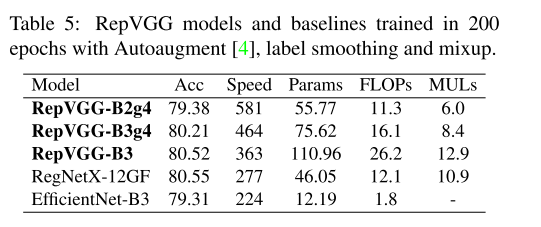
4.2 Structural Re-parameterization is the Key
表6消融实验证明了3分支结构的重要性,Identity branch 和 1 x 1 branch。
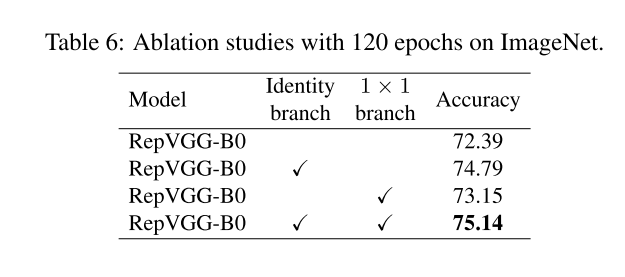
基于RepVGG-B0 baseline的实现比较,需要注意的是加入了ReLU 虽然可以提升性能,但是这样就无法在inference-time 转换为single branch的形式(由于加入了非线性的操作,卷积的可加性就无法使用了)。
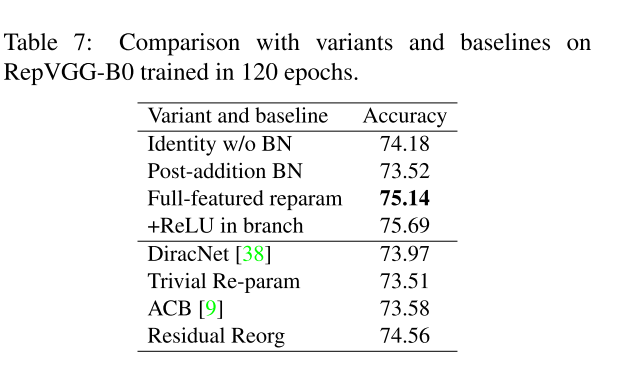
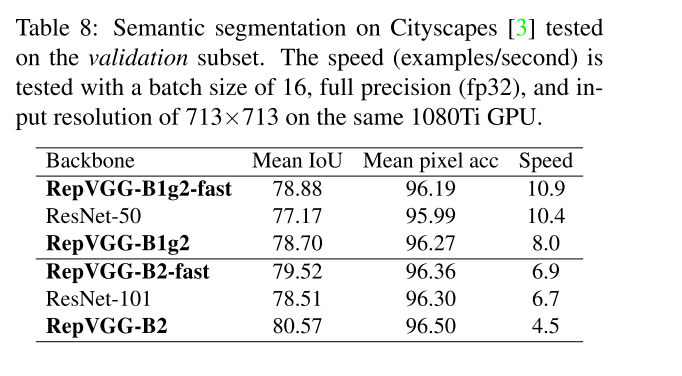
4.3 Semantic Segmentation
Reference
https://zhuanlan.zhihu.com/p/344324470