排序算法一之冒泡排序，看完这篇文章一定让你理解

1.算法思想

它重复地走访过要排序的元素列，依次比较两个相邻的元素，如果顺序（如从大到小、首字母从Z到A）错误就把他们交换过来。走访元素的工作是重复地进行直到没有相邻元素需要交换，也就是说该元素列已经排序完成。

这个算法的名字由来是因为越小的元素会经由交换慢慢“浮”到数列的顶端（升序或降序排列），就如同水中的气泡上浮到顶端一样，故名“冒泡排序”。

2.算法步骤

• 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
• 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
• 针对所有的元素重复以上的步骤，除了最后一个。
• 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

3.动态演示

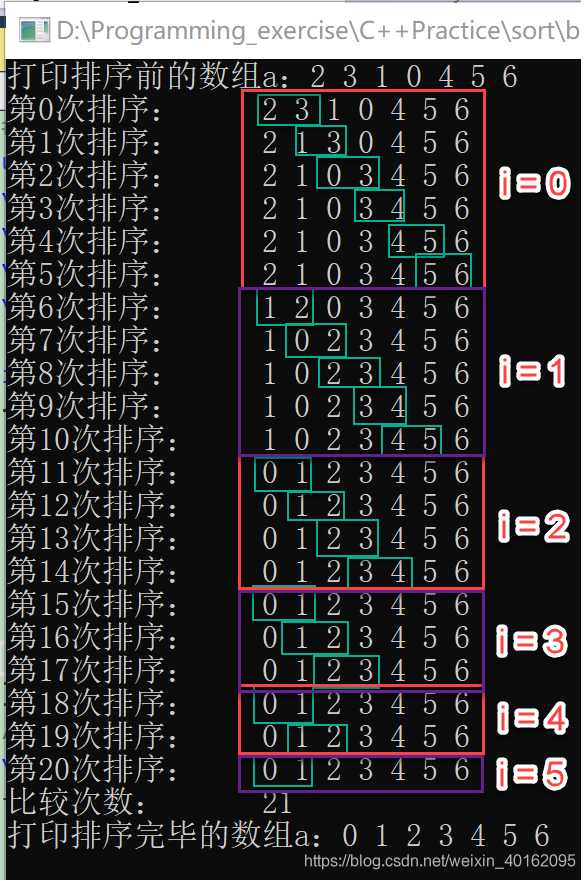
4.无优化冒泡排序

c++代码

//小的数像水泡浮在上面
void sort(int* b, int n)
{
    
    
	int count = 0;
	//n个数比较只需要比较n-1次，因为比较是两个数之间进行的，比如两个数比较只需要比较1次。
	for (int i = 0; i < n - 1; i++)
	{
    
    
		//可以这么理解当大的数沉底后，就不再参与排序了，循环1次，找出此轮中最大的数放在该轮比较的最底部，
		//下一轮找出剩下数据中的最大值，并排到该轮最底部，排序了i次后，就有i个数退出排序，就只剩下n-1-i个数待排，这就是n-1-i的由来
		for (int j = 0; j < n - 1 - i; j++)
		{
    
    
			if (b[j] > b[j + 1])
			{
    
    
				int temp = 0;
				temp = b[j];
				b[j] = b[j + 1];
				b[j + 1] = temp;
			}
			printarray(b, n, count);
			count++;
		}
	}
	cout << "排序次数：\t" << count << endl;
}

主函数–测试例程

#include <iostream>
using namespace std;
void sort(int* b, int n);//未优化冒泡排序
void sort1(int* b, int n);//优化外层循环冒泡排序
void sort2(int* b, int n);//优化内层循环
void printa(int* b, int n);
void printarray(int* b, int n, int count);
int main()
{
    
    
	int a[7] = {
    
     2,3,1,0,4,5,6 };
	cout << "打印排序前的数组a：";
	printa(a, 7);
	sort(a, 7);//调用排序函数
	//sort1(a, 7);//调用排序函数
	//sort2(a, 7);//调用排序函数
	cout << "打印排序完毕的数组a：";
	printa(a, 7);
 	return 0;
}
void printarray(int* b, int n,int count)
{
    
    
	cout << "第" << count << "次排序：\t";
	for (int i = 0; i < n; i++)
	{
    
    
		cout << b[i] << " ";
	}
	cout << endl;
}
void printa(int* b, int n)
{
    
    
	for (int i = 0; i < n; i++)
	{
    
    
		cout << b[i] << " ";
	}
	cout << endl;
}

测试结果：

5.算法优化1（优化外层循环）

参考自：https://blog.csdn.net/yanxiaolx/article/details/51622286
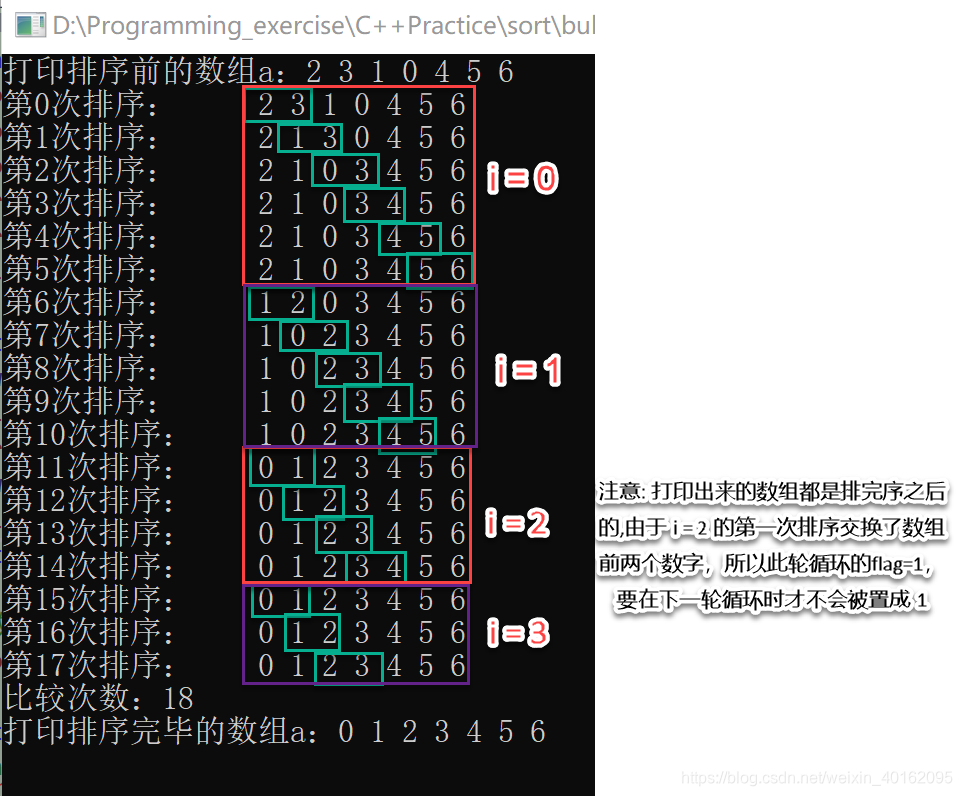
若在某一趟排序中未发现气泡位置的交换，则说明待排序的无序区中所有气泡均满足轻者在上，重者在下的原则，因此，冒泡排序过程可在此趟排序后终止。为此，在下面给出的算法中，引入一个标签flag，在每趟排序开始前，先将其置为0。若排序过程中发生了交换，则将其置为1。各趟排序结束时检查flag，若未曾发生过交换则终止算法，不再进行下一趟排序。

c++代码

//优化外层循环
void sort1(int* b, int n)
{
    
    
	int count = 0;
	for (int i = 0; i < n - 1; i++)
	{
    
    
		//每次遍历标志位都要先置为0，才能判断后面的元素是否发生了交换
		int flag = 0;
		for (int j = 0; j < n - 1 - i; j++)
		{
    
    
			if (b[j] > b[j + 1])
			{
    
    
				int temp = 0;
				temp = b[j];
				b[j] = b[j + 1];
				b[j + 1] = temp;
				flag = 1;
			}
			printarray(b, n,count);
			count++;
		}
		//判断标志位是否为0，如果为0，说明后面的元素已经有序，就直接return
		if (flag == 0)
		{
    
    
			cout << "比较次数：" << count << endl;
			return;
		}
	}
}

测试结果

性能分析（算法时间、空间复杂度、稳定性）

（1）时间复杂度

在设置标签flag变量之后：

当原始序列“正序”排列时，冒泡排序总的比较次数为n-1，移动次数为0，也就是说冒泡排序在最好情况下的时间复杂度为O(n)；

当原始序列“逆序”排序时，冒泡排序总的比较次数为n(n-1)/2，移动次数为3n(n-1)/2次，所以冒泡排序在最坏情况下的时间复杂度为O(n^2)；

当原始序列杂乱无序时，冒泡排序的平均时间复杂度为O(n^2)。

（2）空间复杂度

冒泡排序排序过程中需要一个临时变量进行两两交换，所需要的额外空间为1，因此空间复杂度为O(1)。

（3）稳定性

 冒泡排序是就地排序。
 冒泡排序在排序过程中，元素两两交换时，相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。

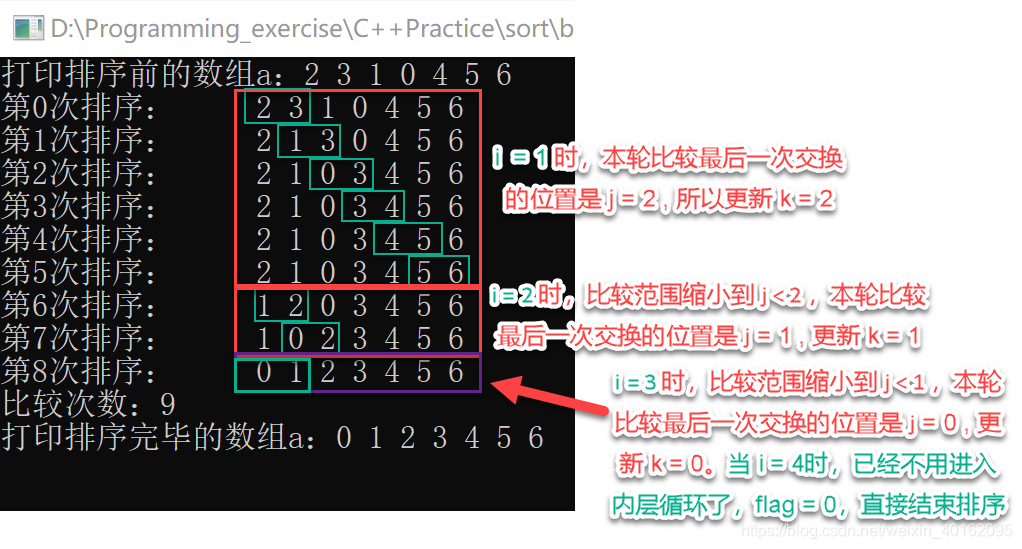
6.算法优化2（优化内层循环）

记住每轮(相对于i来说，i=0是第0轮，i=1是第一轮，以此类推)最后一次交换发生位置pos，在每轮扫描中，记住最后一次交换发生的位置pos，该位置之后的相邻记录均已有序。下一轮排序开始时，R[1…pos-1）是无序区，R[pos…n]是有序区。记住最后一次交换发生的位置pos，从而减少排序的趟数。

c++代码

//优化内层循环
void sort2(int* b, int n)
{
    
    
	int count = 0;
	int k = n - 1;
	for (int i = 0; i < n - 1; i++)
	{
    
    
		//每轮遍历标志位都要先置为0，才能判断后面的元素是否发生了交换
		int flag = 0, pos = 0;
		for (int j = 0; j < k; j++)
		{
    
    
			if (b[j] > b[j + 1])
			{
    
    
				int temp = 0;
				temp = b[j];
				b[j] = b[j + 1];
				b[j + 1] = temp;
				flag = 1;
				pos = j;//一轮循环里最后一次交换的位置j赋给pos
			}
			printarray(b, n, count);
			count++;
		}
		k = pos;
		//判断标志位是否为0，如果为0，说明后面的元素已经有序，就直接return
		if (flag == 0)
		{
    
    
			cout << "比较次数：" << count << endl;
			return;
		}
	}
}

测试结果