1、 LSTM(Long Short-Term Memory)网络——从RNN网络的扩展
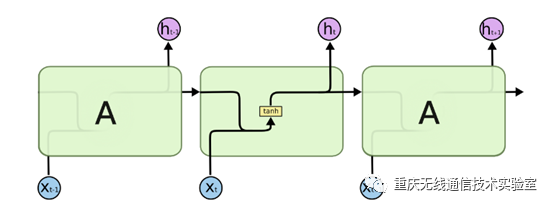
图1 RNN简化模型
RNN网络在深度学习的应用领域已经非常广泛了,简化模型如图1所示,每个序列索引位置t都有一个隐藏状态h(t),图中可以很清晰看出在隐藏状态h(t)由x(t)和h(t−1)得到。得到h(t)后一方面用于当前层的模型损失计算,另一方面用于计算下一层的h(t+1)。但它存在的梯度消失的问题使得其处理起长序列的数据时非常困难,为此而提出LSTM结构网络。
2、LSTM网络结构分析
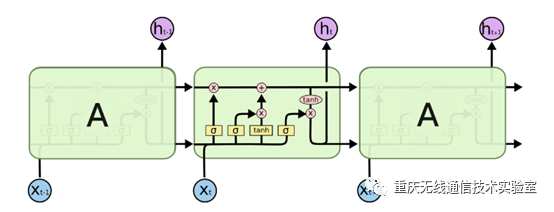
图2 LSTM模型
LSTM的结构如图2所示,可以看到LSTM的结构要比RNN的复杂的多,其结构一般包括遗忘门,输入门和输出门三种门结构以及细胞状态,所以下面对这个结构进行分解分析。
输入门
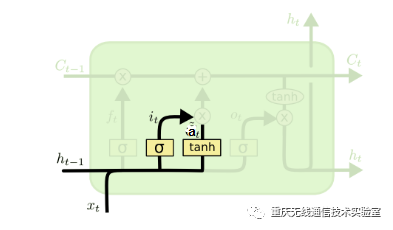
图3 输入门结构图
输入门(input gate)负责处理当前序列位置的输入,分解出来的输入门结构如图3所示,从图中可以看到输入门由两部分组成,第一部分使用了sigmoid激活函数,输出为i(t),第二部分使用了tanh激活函数,输出为a(t), 两者的结果后面会相乘再去更新细胞状态。用数学表达式即为:
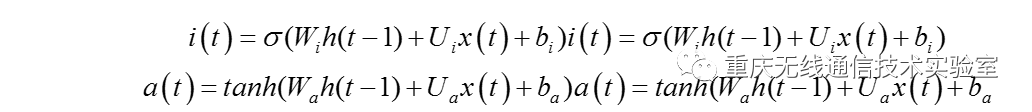
遗忘门
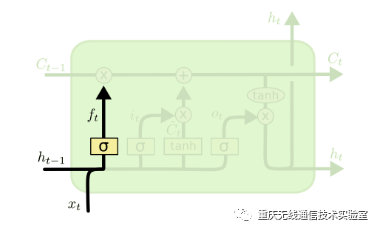
图4 遗忘门结构图
遗忘门在LSTM中即以一定的概率控制是否遗忘上一层的隐藏细胞状态,分解出的的遗忘门结构如图4所示,图中输入的有上一序列的隐藏状态h(t−1)和本序列数据x(t),通过激活函数sigmoid,得到遗忘门的输出f(t)。由于sigmoid的输出f(t)在[0,1]之间,因此这里的输出f{(t)}代表了遗忘上一层隐藏细胞状态的概率。用数学表达式即为:
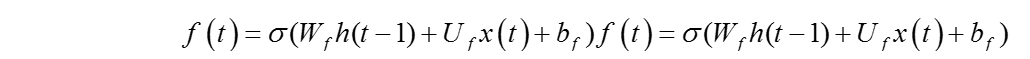
细胞状态
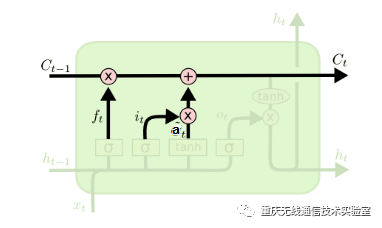
图5 细胞状态结构
分解出细胞状态结构如图5所示,在每个序列索引位置t时刻向前传播的除了和RNN一样的隐藏状态h(t),还多了另一个隐藏状态,如图中上面的长横线。这个隐藏状态我们一般称为细胞状态(Cell State),记为C(t)。其中细胞状态更新是通过遗忘门和输入门的共同作用来完成的,从细胞状态C(t−1)如何得到C(t),从图可以看出细胞状态C(t)由两部分组成,第一部分是C(t−1)和遗忘门输出f(t)的乘积,第二部分是输入门的i(t)和a(t)的乘积,即:
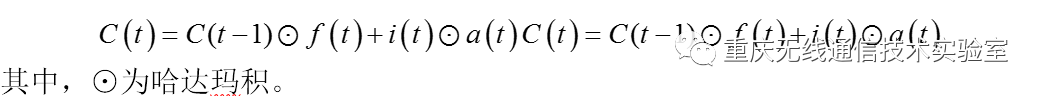
输出门及隐藏状态的更新
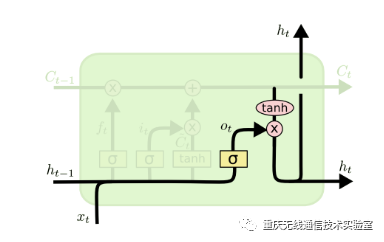
图6 输出门结构
分解出输出门及隐藏状态的结构如图6所示,先来看输出门,可以看出输出门o(t)由上一层的隐藏状态h(t−1)、本序列数据x(t)和激活函数sigmoid所决定的,数学公式可以表达为:
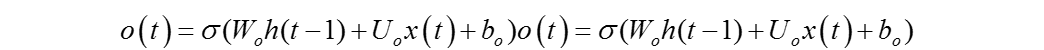
另一方面,本层的隐藏状态由本层的细胞状态C(t)、输出门o(t)以及两个激活函数sigmoid和tanh得到,数学公式可以表达为:
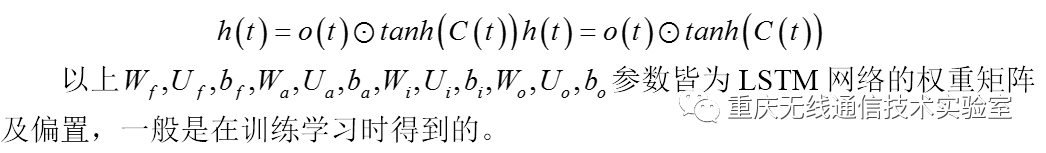
3、 LSTM前向传播算法
比起RNN网络来说,LSTM模型有两个隐藏状态h(t),C(t), 模型参数几乎是RNN的4倍,所以也是更加复杂,其在每个序列索引位置的具体过程为:

4、 代码调试
以下为搭建BiLSTM(Bi-directional Long Short-Term Memory)的部分样例代码,目前还在调试中,有兴趣者可供参考。
class BLSTM(nn.Module):
"""
Implementation of BLSTM Concatenation for sentiment classification task
"""
def __init__(self,embeddings, input_dim, hidden_dim, num_layers, output_dim, max_len=40,dropout=0.5):
super(BLSTM,self).__init__()
self.emb =nn.Embedding(num_embeddings=embeddings.size(0),
embedding_dim=embeddings.size(1),
padding_idx=0)
self.emb.weight = nn.Parameter(embeddings)
self.input_dim = input_dim
self.hidden_dim = hidden_dim
self.output_dim = output_dim
# sen encoder
self.sen_len= max_len
self.sen_rnn= nn.LSTM(input_size=input_dim,
hidden_size=hidden_dim,
num_layers=num_layers,
dropout=dropout,
batch_first=True,
bidirectional=True)
self.output =nn.Linear(2 * self.hidden_dim, output_dim)
def bi_fetch(self,rnn_outs, seq_lengths, batch_size, max_len):
rnn_outs =rnn_outs.view(batch_size, max_len, 2, -1)
#(batch_size, max_len, 1, -1)
fw_out =torch.index_select(rnn_outs, 2, Variable(torch.LongTensor([0])).cuda())
fw_out =fw_out.view(batch_size * max_len, -1)
bw_out =torch.index_select(rnn_outs, 2, Variable(torch.LongTensor([1])).cuda())
bw_out =bw_out.view(batch_size * max_len, -1)
batch_range =Variable(torch.LongTensor(range(batch_size))).cuda() * max_len
batch_zeros =Variable(torch.zeros(batch_size).long()).cuda()
fw_index =batch_range + seq_lengths.view(batch_size) - 1
fw_out =torch.index_select(fw_out, 0, fw_index) # (batch_size, hid)
bw_index =batch_range + batch_zeros
bw_out =torch.index_select(bw_out, 0, bw_index)
outs =torch.cat([fw_out, bw_out], dim=1)
return outs
def forward(self,sen_batch, sen_lengths, sen_mask_matrix):
"""
:paramsen_batch: (batch, sen_length), tensor for sentence sequence
:paramsen_lengths:
:paramsen_mask_matrix:
:return:
"""
''' EmbeddingLayer | Padding | Sequence_length 40'''
sen_batch =self.emb(sen_batch)
batch_size =len(sen_batch)
''' Bi-LSTMComputation '''
sen_outs, _ =self.sen_rnn(sen_batch.view(batch_size, -1, self.input_dim))
sen_rnn =sen_outs.contiguous().view(batch_size, -1, 2 * self.hidden_dim) # (batch,sen_len, 2*hid)
''' Fetch thetruly last hidden layer of both sides
'''
sentence_batch = self.bi_fetch(sen_rnn, sen_lengths, batch_size,self.sen_len) # (batch_size, 2*hid)
representation = sentence_batch
out = self.output(representation)
out_prob =F.softmax(out.view(batch_size, -1))
returnout_prob