信用卡违约用户分析-SGD分类

在DataFountain平台上的用户逾期行为预测竞赛项目。数据来源于某银行公布的网上公开数据集，为银行真实信贷用户信息，应用于信用逾期预测、信用卡评分等业务场景。

import pandas as pd 
import numpy as np
data=pd.read_csv('C:/Users/luoyang/Desktop/信用卡逾期分析/train.csv',\
index_col='CUST_ID',iterator=True)
#csv文件接近500M，全部读入内存不够，iterator参数允许我们读取前N行。

df=data.get_chunk(30000)
#实际上应该设置chunksize参数，然后使用for循环依次训练模式，可以减小内存损耗

在这里插入图片描述
没有缺失数据。

发现只有int、float64、object三种

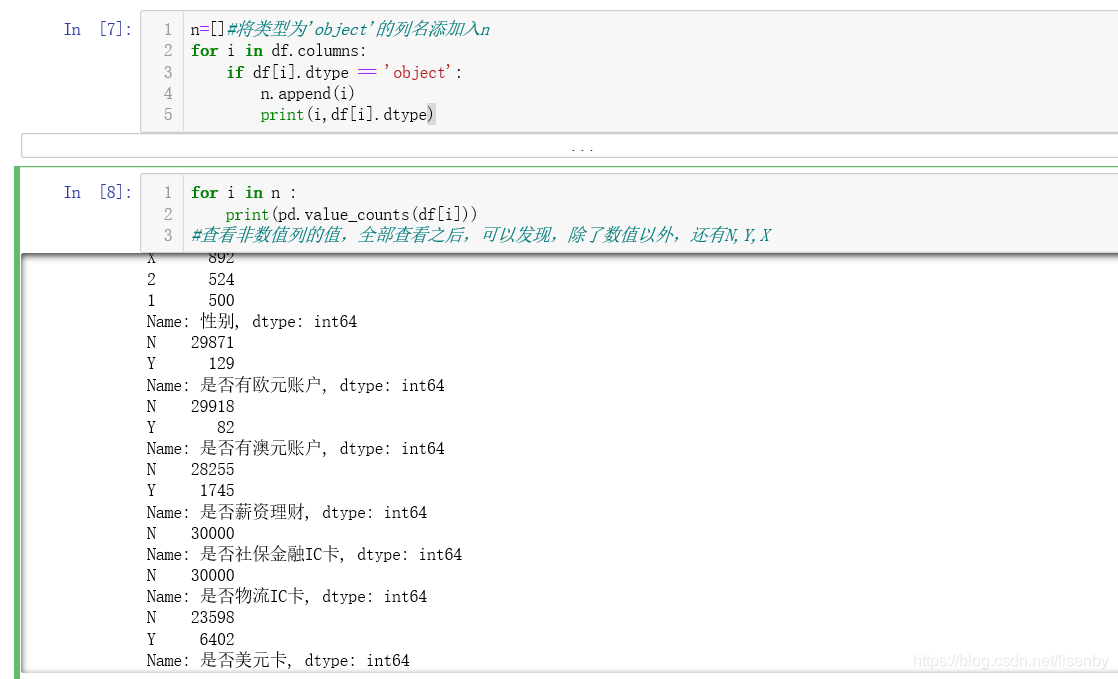
将object列的名称添加入n中，然后查询object列中所有的字段。

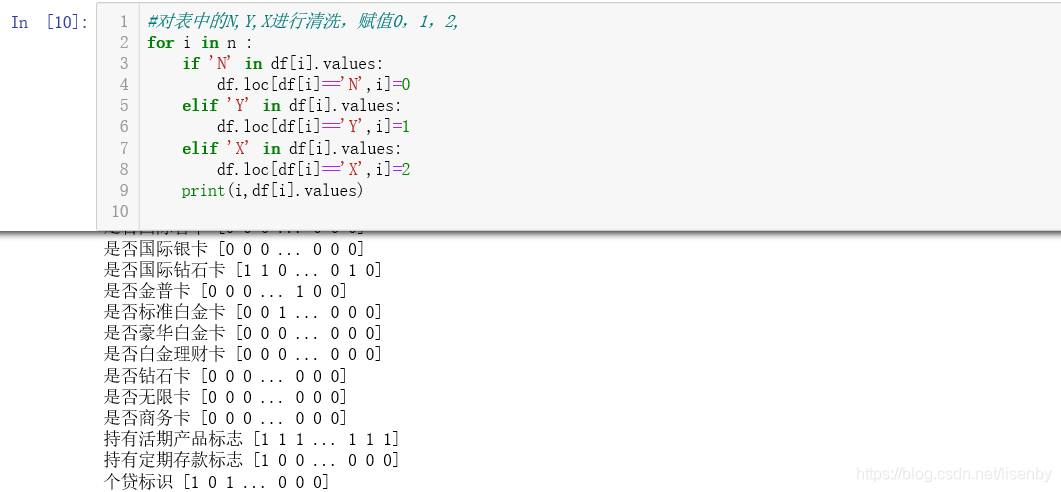
清洗数据，将表达的N，Y,X分别赋值为0，1，2.

在这里插入图片描述
查看一下分类的比例，发现真逾期人员的比例占比为6%左右

X=df.drop(columns='个贷是否逾期').values
y=df.values[:,3].reshape(-1,1)
#将df数据转换如np数组
from sklearn.model_selection import train_test_split
xtr,xte,ytr,yte=train_test_split(X,y,test_size=0.2,random_state=42)
#将数据分为训练集和测试集

#使用随机梯度下降
from sklearn.linear_model import SGDClassifier
from sklearn.preprocessing import StandardScaler,MinMaxScaler
std=StandardScaler().fit(xtr)
min_max=MinMaxScaler().fit(xtr)
xtr_std=std.transform(xtr)
xte_std=std.transform(xte)
xtr_min=min_max.transform(xtr)
xte_min=min_max.transform(xte)
#数据处理
from sklearn.decomposition import PCA
pca=PCA(n_components=100).fit(xtr_min)
xtr_min=pca.transform(xtr_min)
xte_min=pca.transform(xte_min)
#使用PCA算法降维到100
#sgd_clf=SGDClassifier(random_state=42)
sgd=SGDClassifier(random_state=42).fit(xtr,ytr.ravel())
sgd_min=SGDClassifier(random_state=42).fit(xtr_min,ytr.ravel())
sgd_std=SGDClassifier(random_state=42).fit(xtr_std,ytr.ravel())
#使用随机梯度下降算法，这边我个人想查看不做特征处理的数据训练效果和分别作了归一化以及标准差标准化的数据集在SGD算法上的效果

在这里插入图片描述
可以看出在使用归一化的处理方法中效果最好。

在这里插入图片描述

上面是混淆矩阵，精度，召回率，以及F1分数。可以看出真正类比较少见，所以我们可以选择pr曲线。

from sklearn.metrics import precision_recall_curve
y_score=cross_val_predict(sgd_min,xtr_min,ytr.ravel(),cv=3,method='decision_function')
precision,recall,thresholds = precision_recall_curve(ytr,y_score)
#因为真正类率比较少见，所以选择PR曲线，precision_recall_curve计算所有可能的召回率、精度和阈值

import matplotlib.pyplot as plt 
def plot_prc(precision,recall,thresholds):
    plt.plot(thresholds,precision[:-1],'b--',label='Precision')
    plt.plot(thresholds,recall[:-1],'g-',label='Recall')
    plt.xlabel('Threshold')
    plt.legend(loc='upper left')
    plt.ylim([0,1])
    plt.xlim([-8,2.3])
plot_prc(precision,recall,thresholds)
plt.show()
#精度和召回率在阈值为0.8处为最佳权衡

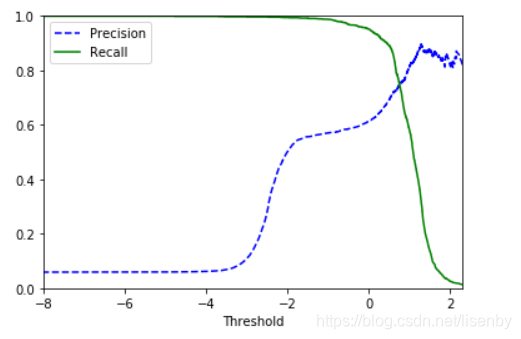
在这里插入图片描述
从图中可以看出最佳权衡为阈值在0。8的时候。

将模型用于预测测试集，然后在最佳权衡上评价预测结果。

上面的代码还没整理，因为用了很多的for循环，会影响性能，且对于这种二分类问题，我还打算继续尝试一下逻辑斯蒂回归以及SVM分类和GBRT等模型在这些数据中的表现，最后选取最优的三个模型然后使用投票分类器进行软投票，以期望获得更好的模型。

信用卡违约用户分析-SGD分类

猜你喜欢