卷积神经网络概述
一个典型的卷积神经网络的整体结构:输入→卷积→ReLU→卷积→ReLU→池化→ReLU→卷积→ReLU→池化→全连接
我们来看一个最简单的例子:“边界检测(edge detection)”,假设我们有这样的一张图片,大小8×8:

图片中的数字代表该位置的像素值,像素值越大,颜色越亮。图的中间两个颜色的分界线就是我们要检测的边界。怎么检测这个边界呢?我们可以设计这样的一个 滤波器(filter,也称为kernel),大小3×3:
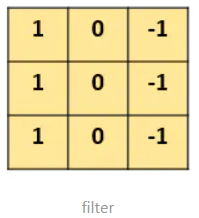
然后,我们用这个filter,往我们的图片上“盖”,覆盖一块跟filter一样大的区域之后,对应元素相乘,然后求和。计算一个区域之后,就向其他区域挪动,接着计算,直到把原图片的每一个角落都覆盖到了为止。这个过程就是 “卷积”。
这里的“挪动”,就涉及到一个步长了,假如我们的步长是1,那么覆盖了一个地方之后,就挪一格,容易知道,总共可以覆盖6×6个不同的区域。
那么,我们将这6×6个区域的卷积结果,拼成一个矩阵:

咦?!发现了什么?
这个图片,中间颜色浅,两边颜色深,这说明咱们的原图片中间的边界,在这里被反映出来了!
从上面这个例子中,我们发现,我们可以通过设计特定的filter,让它去跟图片做卷积,就可以识别出图片中的某些特征,比如边界。
上面的例子是检测竖直边界,我们也可以设计出检测水平边界的,只用把刚刚的filter旋转90°即可。对于其他的特征,理论上只要我们经过精细的设计,总是可以设计出合适的filter的。
我们的CNN(convolutional neural network),主要就是通过一个个的filter,不断地提取特征,从局部的特征到总体的特征,从而进行图像识别等等功能。
这些filter,根本就不用我们去设计,每个filter中的各个数字,不就是参数吗,我们可以通过大量的数据,来 让机器自己去“学习”这些参数嘛。这,就是CNN的原理。
参考:【DL笔记6】从此明白了卷积神经网络(CNN)
卷积神经网络结构
卷积层、池化层、激活函数层:将原始数据映射到隐层特征空间,相当于做特征工程。
全连接层:将学到的“分布式特征表示”映射到样本标记空间,相当于做特征加权。
卷积
含义
用一个卷积核(下图中间矩阵)与原图进行乘积和求和运算,得到原图的特定的局部图像特征(如边缘),用在后面的网络中。
卷积过程
在重叠的图像和卷积核对应元素之间逐个进行乘法运算,按照从左向右、从上到下的顺序。最后相加,得到一个像素值,放在卷积核相应位置。
如果对一幅图用一个和图像大小相同的卷积核,那整张图就会高度浓缩成一个数。
我们不需要详究数学中的卷积运算是怎样的,只要知道CNN中的卷积运行就是过滤器和图像的对应元素相乘再相加就可以了。
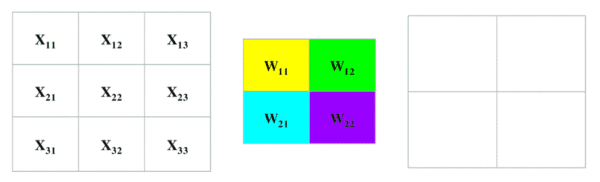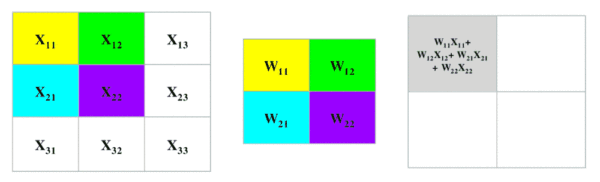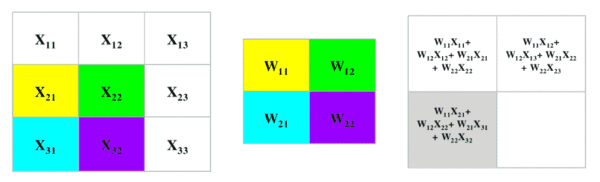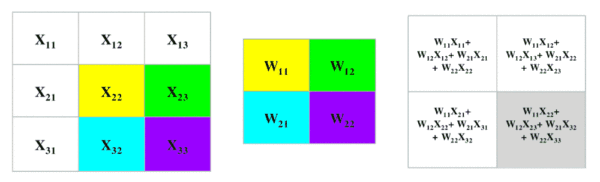
卷积核
上图中,中间2X2的矩阵就叫卷积核,或者叫滤波器。卷积核的大小不是固定的,也不是人定的,是模型待求的参数,在模型训练过程中确定。某些特殊的固定的卷积核叫滤波器。例如对Lena照片用“索伯滤波器”进行卷积后的结果:

“索伯滤波器”如下图,每个值都是固定好的:

在tensorflow中关于卷积层的函数为
tensorflow.nn.conv2d(input, filter, strides, padding)
其中参数分别为:
input:输入数据或者上一层网络输出的结果
filter:卷积核,它的是一个1*4维的参数,例如filter=[5, 5, 3, 96],这4个数字的概念分别是卷积核高度、卷积核宽度、输入数据通道数、输出数据通道数
strides:这是前面所讲的步伐,同卷积核一样,它也是一个1*4维的参数,例如strides=[1, 2, 2, 1],这4个数字分别是batch方向移动的步长、水平方向移动的步长、垂直方向移动的步长、通道方向移动的步长,由于在运算过程中是不跳过batch和通道的,所以通常情况下第1个和第4个数字都是1
padding:是填充方式,主要有两种方式,SAME, VALID,后面会讲什么是填充
相关基础概念
**batch**
当训练数据较多时,为了使数据量在可负载范围内,将数据划分成几部分,即batch。
将这些batch的数据逐一送入计算训练,更新神经网络的权值,使得网络收敛。
参考:深度学习中的Epoch,Batchsize,Iterations,都是什么鬼?
**patch**
在CNN学习训练过程中,不是一次来处理一整张图片,而是先将图片划分为多个小的块,
内核 kernel (或过滤器或特征检测器)每次只查看图像的一个块,这一个小块就称为 patch,
然后过滤器移动到图像的另一个patch,以此类推。
**步长**
每次移动的像素个数。
**图像的深度**
图片是由一个个像素点构成的,所有不同颜色的像素点构成了一副完整的图像,计算机存储图
片是以二进制来进行的。**计算机存储单个像素点所用到的bit为称之为图像的深度。**图像
深度确定彩色图像的每个像素可能有的颜色数,或者确定灰度图像的每个像素可能有的灰度级
数。
在位图中,若每个像素只有一个颜色位,则该像素或为暗或为亮, 即是单色图像(注意,这并
不一定是黑白图像,它只是限制图像只能使用两种色度或颜色)。若每个像素有4个颜色位,位
图则支持2∧4=16种颜色;若每个像素有8个颜色位,则位图可支持256种不同的颜色 。
**图像的通道**
通道表示每个像素点能存放多少个数,例如RGB彩色图像中每个像素点存放三个值,即3通道的。
对于24位的图片,它的像素点取值范围为 0 到 2的24次方,如果是RGB图,24=3*8,我们刚
好就可以用第一个8位存储Red值,第二个存储Green值,第三个存储Blue值。2的8次方刚好
是255,所以Red值、Green值、Blue值的范围都是0-255。所以我们一般看到的RGB值都是(0-
255,0-255,0-255)这样的值。
如下图所示,该图中共画了4*4个像素,RGB三个通道,图像的深度是24位,即用24位表示一
个像素点,该像素点前8位表示R值,中间8位表示G值,后面8位表示B值,R值、G值、B值的
变化范围是0-255。

参考:
图像基础-像素,分辨率,深度,通道理解
图像的深度和通道概念
图像的通道和深度
多通道图片的卷积

如下图所示,同一个通道权重共享,不同通道权重不共享,当图片的通道增加到3维,卷积核也增加到三维。做卷积时,每层和相应权重相乘,最后将各层累加到一起得到一个值。

如下图所示,每增加一个卷积核,就得到一个Feature Map。将所有卷积核卷积得到的Feature Map按顺序堆叠,就得到卷积层的最终输出。这个输出有多少层,即是输出通道是多少。

从下图可以看出,过滤器的通道(即过滤器的层数,在图中是3)必须和输入图像的通道数量一致,卷积层输出通道的个数(即卷积层的层数,在图中是4)和卷积核的个数相同。

加上一个Relu激活函数后:

填充
在图像周围添加零,让我们可以在更多位置叠加过滤器,使输出图像与输入图像的大小相同。

两种填充方式
VALID:向下取整,不填充
SAME:向上取整,用0填充
卷积网络输出大小计算公式
out = (in - filter_size + 2*padding)/strides + 1
out:输出图片大小
in:输入图片大小
filter_size:卷积核大小
padding:padding大小
strides:步长大小
非线性层
在非线性层中,我们大多时候使用 ReLU 激活函数,或者 S 型激活函数和 Tan-H 激活函数。 ReLU 激活函数会为输入图像中的每个负值返回 0,每个正值则返回同样的值。

池化
图像中的相邻像素倾向于具有相似的值,因此通常卷积层相邻的输出像素也具有相似的值。这意味着,卷积层输出中包含的大部分信息都是冗余的。池化层通过采样方法可以对像素进行降维,减少冗余。
池化一般通过简单的最大值、最小值或平均值操作完成。以下是池大小为2的最大池层的示例:
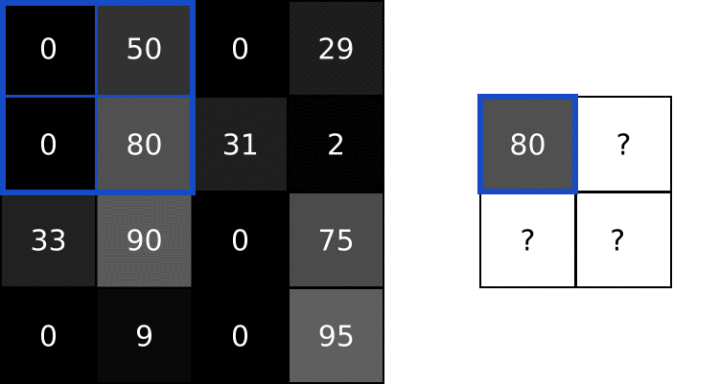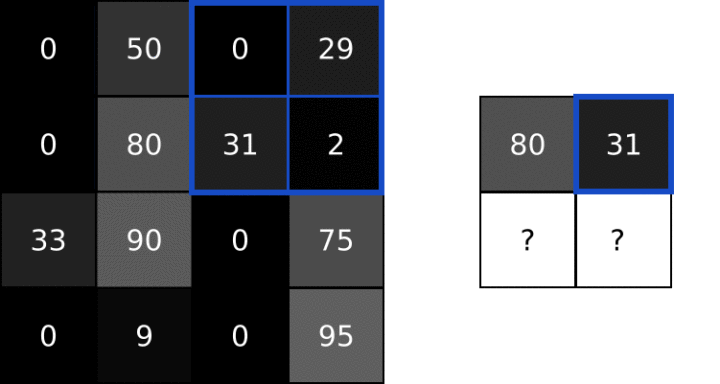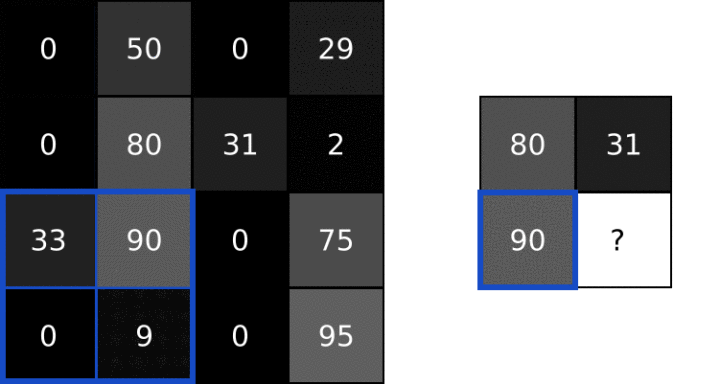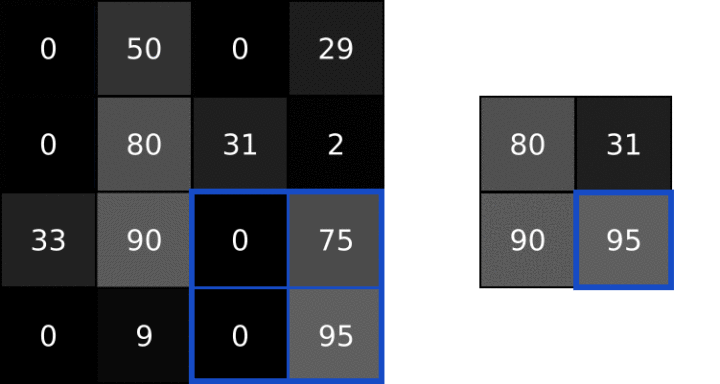
每一次池化使图像缩小为原来的1/2倍。
池化padding的两种方式


参考:TensorFlow中CNN的两种padding方式“SAME”和“VALID”
tensorflow中池化运算的函数
tensorflow.nn.max_pool(value, ksize, strides, padding)
从函数的参数即可看出来,它和卷积层非常相似,它的参数概念分别是,
value:输入数据或者上一层网络输出的结果
ksize:卷积核,它的是一个1*4维的参数,例如ksize=[1, 3, 3, 1],这4个数字的概念分别是batch维度池化窗口、池化窗口高度、池化窗口宽度、通道维度窗口尺寸,由于在batch和通道维度不进行池化,所以通常情况下第1和第4个元素为1
strides:这和卷积层中相同
padding:这和卷积层中的也相同
整个过程
先把x_image和权值向量 W_conv1进行卷积,加上偏置项b_conv1,然后应用ReLU激活函数,最后进行max pooling。tf过程如下:
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = max_pool_2x2(h_conv1)
Dropout
在不同的训练过程中随机扔掉一部分神经元。也就是让某个神经元的激活值以一定的概率p,让其停止工作,这次训练过程中不更新权值,也不参加神经网络的计算。但是它的权重得保留下来(只是暂时不更新而已),因为下次样本输入时它可能又得工作了。

tf.nn.dropout(x,keep_prob,noise_shape=None,seed=None,name=None)
函数说明:
上面的方法中常用的是前面两个参数:
第一个参数x:指输入
第二个参数keep_prob:控制神经元在训练中被dropout的比例,即设置某些神经元被保留下来的概率,在初始化时keep_prob是一个占位符,keep_prob = tf.placeholder(tf.float32) 。tensorflow在run时设置keep_prob具体的值,例如keep_prob: 0.5
第三个参数noise_shape:一个1维的int32张量,代表了随机产生"保留/丢弃"标志的shape
seed :整形变量,随机数种子
name :名字,没什么实际用处。
总结:dropout()函数就是使tensor中某些元素变为0,其它没变0的元素变为原来的1/keep_prob大小。
参考:tf.nn.dropout()介绍
全连接层
作用:将特征空间映射到标签
例如:训练数据是3维的猫和狗的图片,标签是一维的01和10。经过CNN的多次卷积和池化后仍然是3维的(通常情况下),此时为了计算梯度必须和1维的标签对应上,所以用全连接将3维变成1维。
缺点:会丢失一些位置特征,不适合做目标检测的任务,适合做分类
参考:全连接层的作用是什么?
全连接层的两种方式
一种是将最后一个卷积层的输出压平,然后用多个与该输出相同大小的卷积核对该输出层进行卷积,得到全连接层的各个神经元。
例如下左图:
卷积层输出是:1x3,则卷积核大小:1x3
全连接层是:1x4,则卷积核总大小:1x3x4,共有4个1x3的卷积核对1x3的输出进行卷积,得到全连接层的4个神经元。

一种如下过程所示:
这种方式没有将最后一个卷积层的输出压平。而是直接将3x3x5的卷积层输出,转换成1x4096的全连接层。详细过程如下。
如下两幅图,上面图是卷积、池化、激活层,最后得到激活函数的输出。
下面图是由激活函数的输出层转到全连接层。


它是怎么样把3x3x5的输出,转换成1x4096的形式?

很简单,可以理解为在中间做了一个卷积:
用一个3x3x5大小的卷积核去卷积这个3x3x5大小的激活函数的输出(每层对应元素相乘再相加,最后5层的元素再相加,得到一个值),得到一个全连接层的神经元。
卷积4096次,就得到1x4096的全连接层。
所以我们一共有3x3x5x4096个参数。

我们实际就是用一个3x3x5x4096的卷积层去卷积激活函数的输出
参考:CNN 入门讲解:什么是全连接层(Fully Connected Layer)?
全连接层形式化表达
卷积、池化两层是提取特征,特征提取完后得到新的图像集合,就是下图中的最左边的x1、x2、x3。全连接层的作用类似于y = Wx,已知像素x1、x2、x3,类别是y,训练出权值W。
卷积层的卷积核、全连接层的权值W都是由训练集训练后得出,都是参数。

全连接(fully connected layers,FC)的核心操作就是矩阵向量乘积 y = Wx。全连接层中的每个神经元与其前一层的所有神经元进行全连接.全连接层可以整合卷积层或者池化层中具有类别区分性的局部信息.为了提升 CNN网络性能,全连接层每个神经元的激励函数一般采用ReLU函数。
全连接的参数实在是太多了,你想这张图里就有201212100个参数,前面随便一层卷积,假设卷积核是77的,厚度是64,那也才7764,所以现在的趋势是尽量避免全连接,目前主流的一个方法是全局平均值。也就是最后那一层的feature map(最后一层卷积的输出结果),直接求平均值。有多少种分类就训练多少层,这十个数字就是对应的概率或者叫置信度。

对全连接层(fully connected layer)的通俗理解
softmax
不只求出最大值,而是求出每个类别的可能性。

交叉熵损失函数
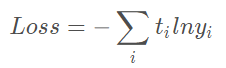
交叉熵损失函数是一个凹函数,在用梯度下降法求解模型参数时,用Loss函数作为目标函数,能够更快收敛。
相比于分类错误率和MSE,Loss更能捕捉到模型之间预测效果之间的差异。同时,它不仅可以很好的衡量模型的效果,又可以很容易的的进行求导计算。
详细解释:损失函数 - 交叉熵损失函数
tf.nn.sparse_softmax_cross_entropy_with_logits 函数和tf.nn.softmax_cross_entropy_with_logits_v2 函数
两者都是计算交叉熵的。不同点:
- tf.nn.sparse_softmax_cross_entropy_with_logits 函数直接利用全连接层输出的标签结果,处理的是真实标签,没有经过softmax函数,而是直接在这个函数中进行softmax函数的计算,也就是这个函数包含了softmax函数和计算交叉熵的功能。
- tf.nn.softmax_cross_entropy_with_logits_v2 函数处理的是one-hot的标签。
真实标签: shape为[batch_size, num_classes],如多分类的label[0,2,1,0…]处理后的标签为[[1,0,0],[0,0,1],[0,1,0],[1,0,0]…];除了one-hot表示,labels的每一行也可以是一个概率分布,每个数值表示属于每个类别的概率。
参考:TensorFlow之计算交叉熵的函数 tf.nn.sparse_softmax_cross_entropy_with_logits
参考:tensorflow 笔记10:tf.nn.sparse_softmax_cross_entropy_with_logits 函数
反向传播算法(BP算法)
梯度下降法
总结一下卷积神经网络的结构
一 卷积运算:前一层的特征图与一个可学习的卷积核进行卷积运算,卷积的结果经过激活函数后的输出形成这一层的神经元,从而构成该层特征图,也称特征提取层,每个神经元的输入与前一层的局部感受野相连接,并提取该局部的特征,一旦该局部特征被提取,它与其它特征之间的位置关系就被确定。
二 池化运算:它把输入信号分割成不重叠的区域,对于每个区域通过池化(下采样)运算来降低网络的空间分辨率,比如最大值池化是选择区域内的最大值,均值池化是计算区域内的平均值。通过该运算来消除信号的偏移和扭曲。
三 全连接运算:输入信号经过多次卷积核池化运算后,输出为多组信号,经过全连接运算,将多组信号依次组合为一组信号。
四 识别运算:上述运算过程为特征学习运算,需在上述运算基础上根据业务需求(分类或回归问题)增加一层网络用于分类或回归计算。
示例图如下所示:

参考:CNN(卷积神经网络)是什么?有何入门简介或文章吗?
CNN进行分类:将CNN的网络结构及整个运行过程讲解的很清楚。在训练模型时,针对每一张图片,都会进行一次前向传导、损失函数、后向传导以及参数更新的过程,这个过程称为一个学习周期。
卷积神经网络整体训练过程

第一阶段,向后传播阶段
1、先初始化随机权重W0,随机选取一张(批)图片的数据与权重喂入网络,得到Y值,然后计算Loss0
在此阶段,信息从输入层经过逐级的变换,传送到输出层。这个过程也是网络在完成训练后正常运行时执行的过程。在此过程中,网络执行的是计算(实际上就是输入与每层的权值矩阵相点乘,得到最后的输出结果):
Op=Fn(…(F2(F1(XpW(1))W(2))…)W(n))
第二阶段,向前传播阶段
2、根据Loss0,利用前向传播算法更新权重,得到W1。再随机选第二张(批)图片和新的权重W1过网络,计算Y值,计算Loss1。
3、重复第2步。
当把数据集分批次送入网络进行训练时,tensorflow的输入张量是4维的,[batchsize,高度,宽度,通道数],第一维就是batch的大小。tensorflow会将这批图片一起训练,然后统一计算Loss,不过这样对内存要求就很大了。
分批训练和单张图片训练的过程类似,不过是多了一个batchsize维度,tf会统一对这个batch的图片进行矩阵运算,但是这个batch内的图片还是分成一张张进行卷积池化的。
其他相关概念
过拟合
指的是给定一堆数据,这堆数据带有噪声,利用模型去拟合这堆数据,可能会把噪声数据也给拟合了,一方面会造成模型比较复杂(想想看,本来一次函数能够拟合的数据,现在由于数据带有噪声,导致要用五次函数来拟合,多复杂!),另一方面,模型的泛化性能太差了(本来是一次函数生成的数据,结果由于噪声的干扰,得到的模型是五次的),遇到了新的数据让你测试,你所得到的过拟合的模型,正确率是很差的。
本来解空间是全部区域,但通过正则化添加了一些约束,使得解空间变小了,甚至在个别正则化方式下,解变得稀疏了。
标准化
在训练模型过程中,输入值的分布是不固定的,有的值大,有的值小,但是学习率是固定的。当输入值大,但是学习率小时,就会导致收敛过慢,模型训练效率低。
有没有什么优化方法呢?
优化方法就是标准化。因为我们学习的是数据的分布特征,而不是数据的绝对值,因此可以将模型输入值标准化到一个范围内,比如[0,1]内。这就是Batch Normalization,简称BN。由大名鼎鼎的inception V2提出。它在每个卷积层后,使用一个BN层,从而使得学习率可以设定为一个较大的值。使用了BN的inceptionV2,只需要以前的1/14的迭代次数就可以达到之前的准确率,大大加快了收敛速度。
深度学习模型训练过程
正则化
类似于带约束的目标函数,通过给目标函数带上约束,可以缩小解的范围,防止过拟合。通俗来说就是约束化、限制化。
例如原目标函数如下图所示:
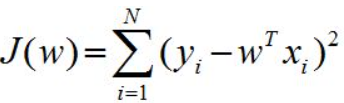
加上约束条件:
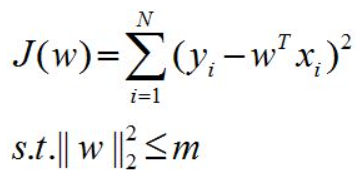
通过拉格朗日乘子变换:
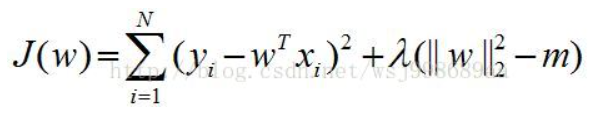
lamda即是正则化因子,如果它变大了,说明目标函数的作用变小了,正则化项的作用变大了,对参数的限制能力加强了,这会使得参数的变化不那么剧烈,直接的好处就是避免模型过拟合。