高数_第一章_第二节_极限

极限（重难点）

一、考试概要

极限的概念

1）数列的极限

$$\begin{gathered} \epsilon 限制两者的范围，N用来表示数列以后的项 \\ 部分列极限必须相等才能成为数列极限存在的充要条件 \end{gathered}$$
例题：

1）

2）

两个常用结论，用来函数极限也是对的

2）函数的极限

1. 极限的性质

函数极限是x->∞或者是x->特定的值

1)当变量趋向于∞的情况：

tips:

区别于数列极限，数列极限的n因为只能取正整数，所以默认趋向+∞，函数极限可以趋向于正无穷或者负无穷

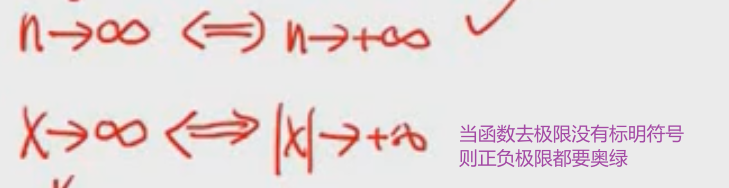
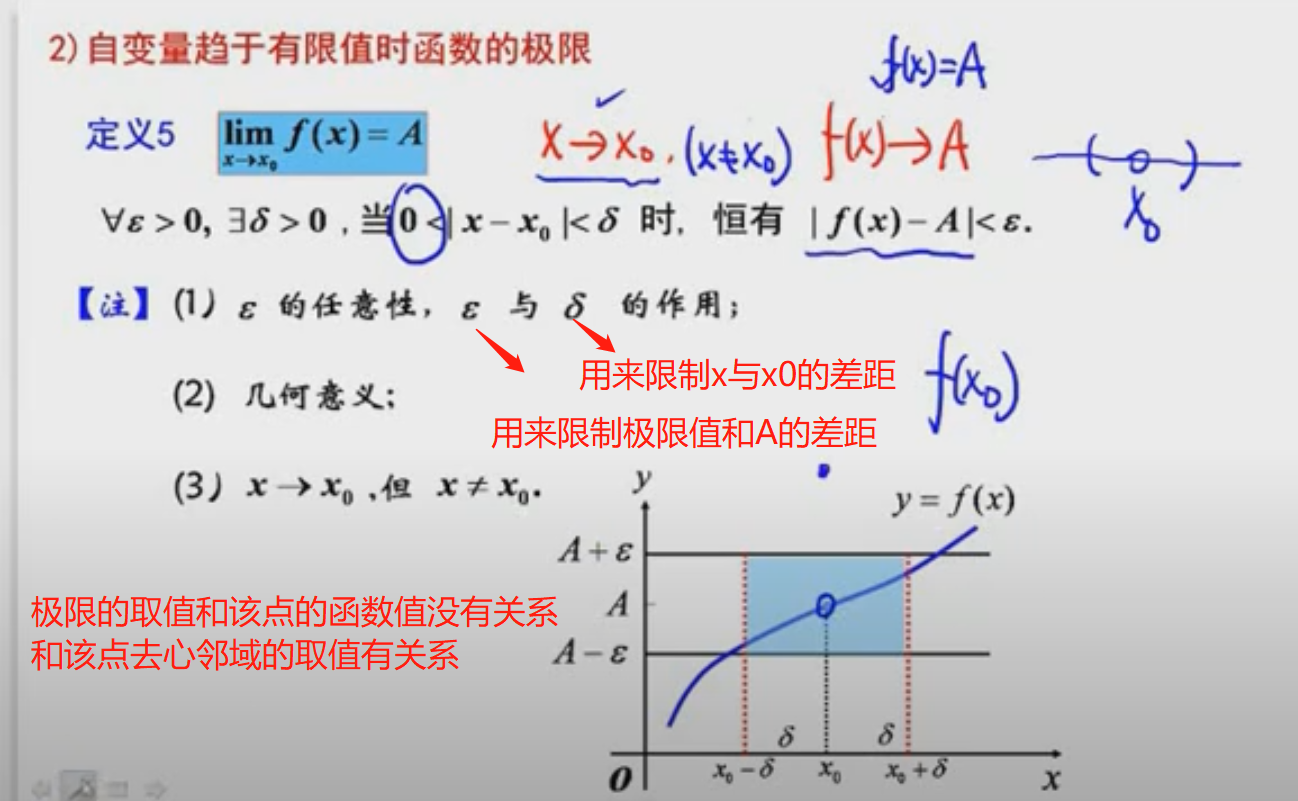
经典错误

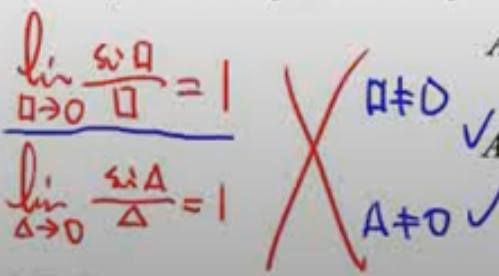
错误原因：

虽然自变量趋向于0，但是无法保证自变量不等于0

类似于：
$$\underset{x\to 0}{\lim }\frac{\sin (x\sin \frac{1}{x})}{x\sin \frac{1}{x}}$$
之所以不存在是因为，分母为0函数没有意义。

但在0点的去心邻域内有很多个分母为0的点。

左右极限

需要用左右极限来求极限的情况

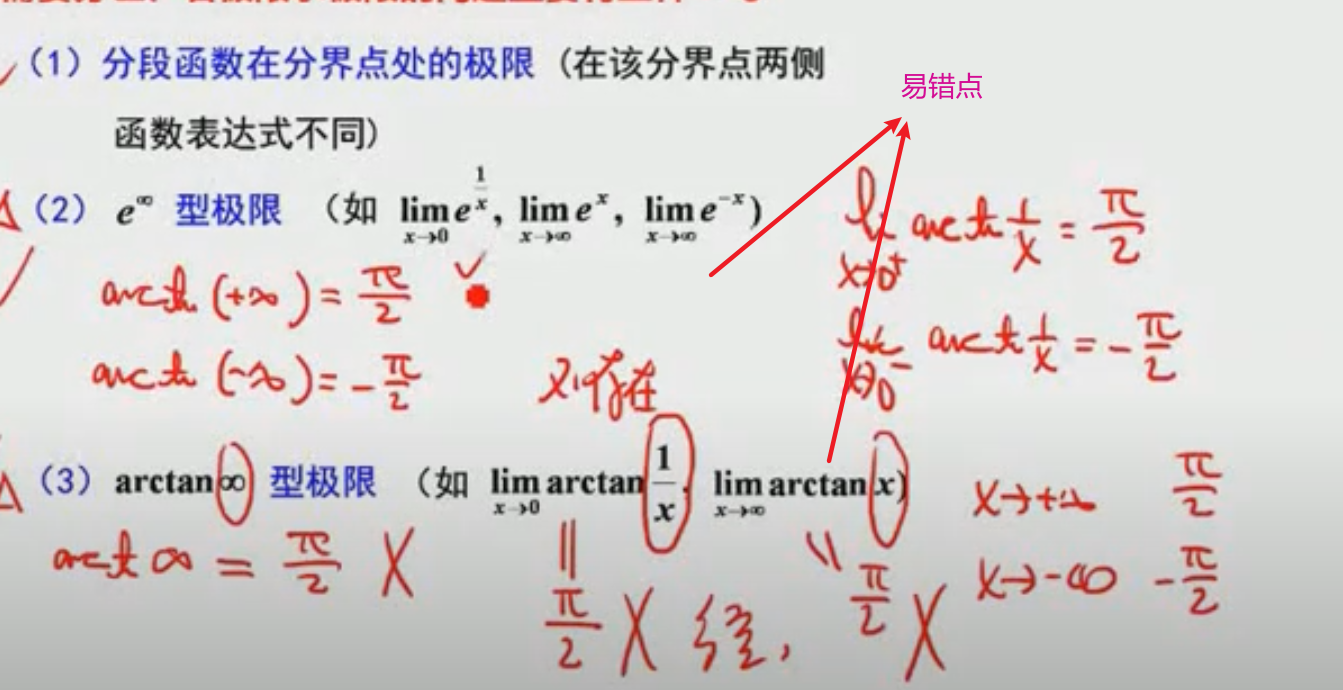
极限的性质

1. 有界性

   

   如何理解：

   数列收敛的结果是：当n趋向0的极限存在

   根据极限的几何意义，N项以后的所有点都落在a的邻域内，所以N项以后的都有界

   在N项之前的项是有限项，有限项一定是有最大值的，所以如果数列收敛，则数列一定有界

   

   有界是数列收敛的必要条件，不充分

   

   函数极限有界性：

   

   2、保号性

   数列极限的保号性：

   

   如果从极限值保数列值，应该不带等号：

   因为根据几何意义，数列值会落在极限值的左右两侧，如果极限值是=0，则有可能有的数列值会落在0点左侧，就无法保证xn>=0

   如果从数列值保极限值，应该带等号：

   如果数列值都是>0，但无法保证极限值不等于0

   3、极限值和无穷小的关系

   

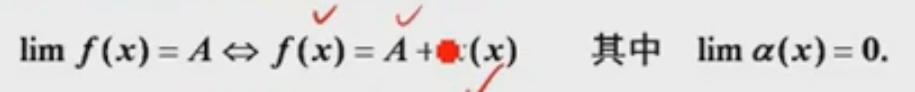
   极限的存在准则

   数列极限的存在准则

   

   夹逼比较适合用于：n项和

   单调有界准则比较适用于：递推关系

   取整函数的基本不等式：

   

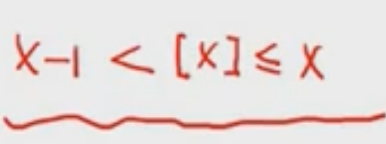
无穷小

无穷小量：

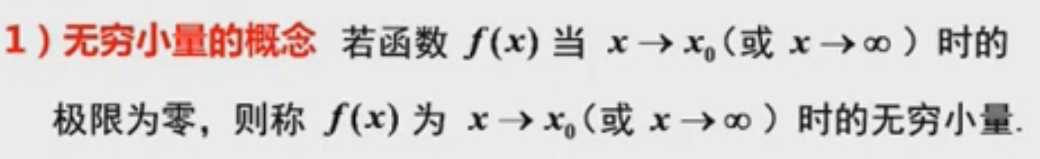
无穷小量就是函数极限为0，当x趋向x0或者x趋向于无穷的时候

无穷小量的比较：

无穷小的性质：

无穷大

无穷大的概念：

常见无穷大量的比较：

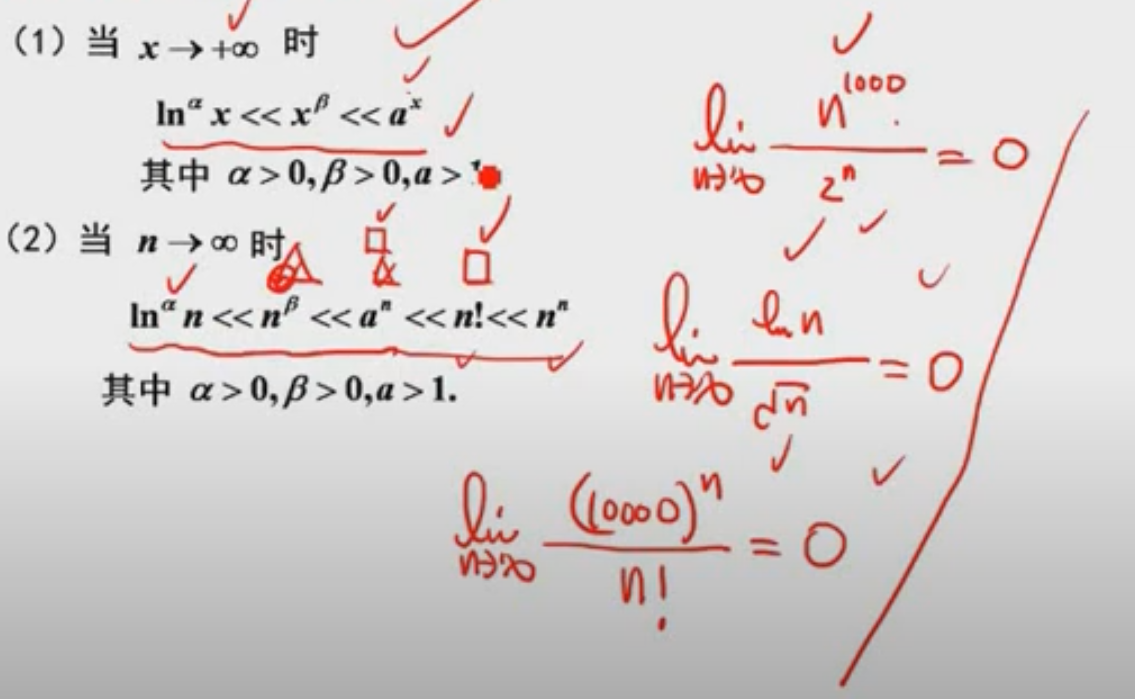
无穷大量的性质：

无穷大和无界的关系：

无穷大是N项以后都很大，无界是有很大

无穷大和无穷小的关系：

二、常考题型

题型一、极限的概念性质、存在准则

(概念比较常考选择题)

题型二、求极限

方法一、利用基本极限求极限

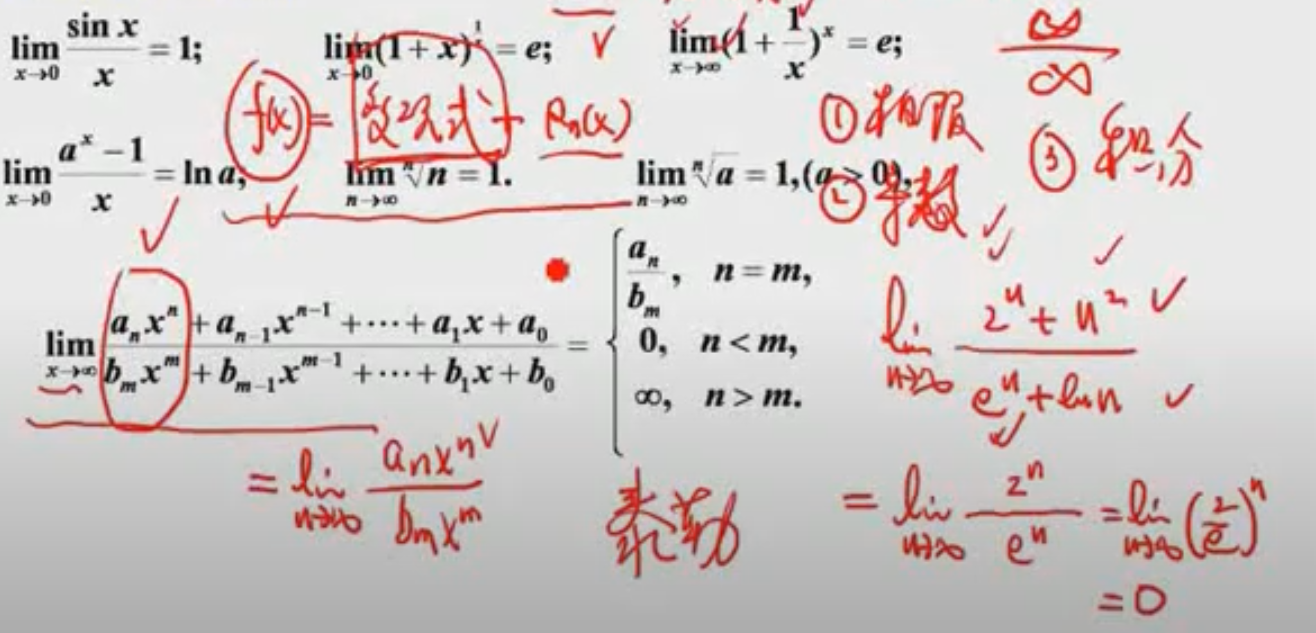
方法二、利用等价代换求极限

方法三、利用有理运算法则

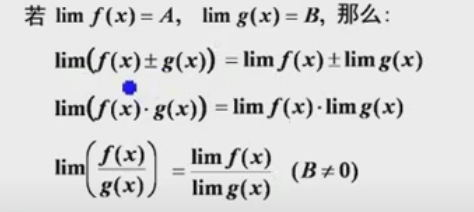
举例：

不存在+不存在 = 存在：
$$\underset{x\to \infty }{\lim }x+\underset{x\to \infty }{\lim }-x=0存在$$
3）

存在 * 不存在 = 存在：
$$\underset{x\to \infty }{\lim }x\ast \underset{x\to \infty }{\lim }\frac{1}{x}=1存在$$
4）

不存在 * 不存在 = 存在：
$$\underset{n\to \infty }{\lim }(-1{)}^n\ast \underset{n\to \infty }{\lim }(-1{)}^n=1存在$$
常用结论：

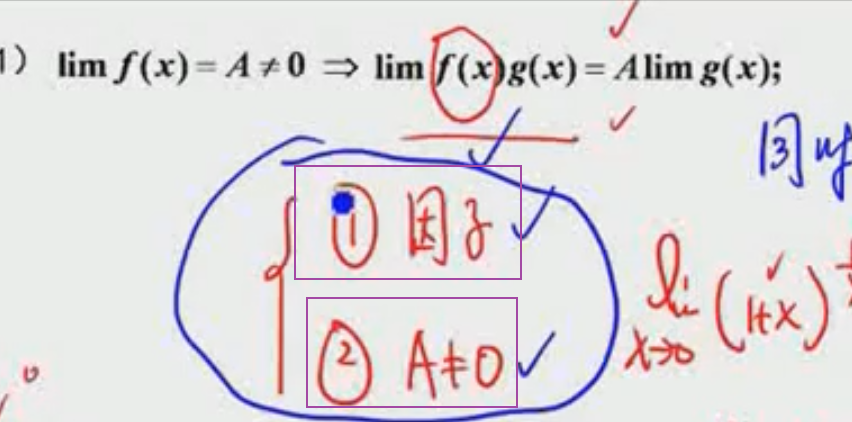
1. 极限的非0因子极限可以先求出来

2. 分式极限，分母趋向于0，分子也趋向于0，不可以用反证法的原因是，f(x)极限为0的反证条件是，f(x)极限为非0实数或不存在

方法四、利用洛必达法则求极限

方法五、使用泰勒公式求极限

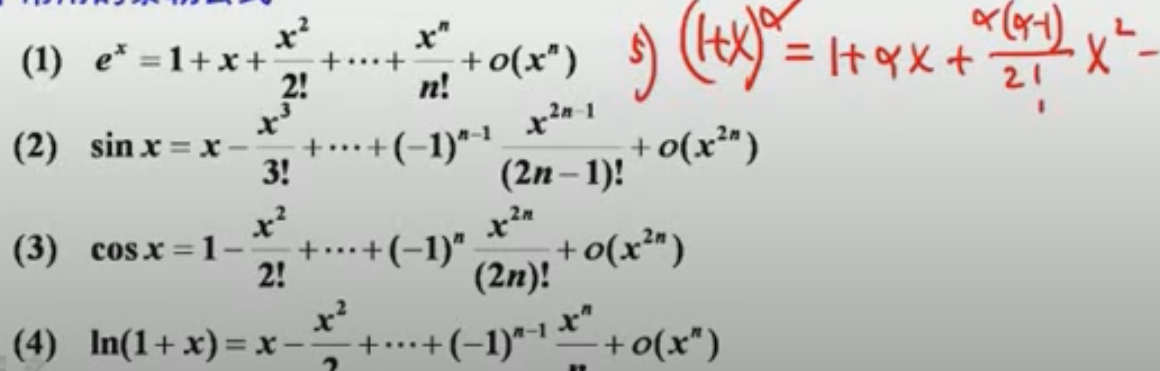
方法六、利用夹逼定理求极限

方法七、利用单调有界准则求极限

题型三、无穷小量阶的比较

一般就是
$$\frac{0}{0}$$
常用方法：

洛必达

等价代换

泰勒公式