排列熵、模糊熵、近似熵、样本熵的原理及MATLAB实现之样本熵

说明：“本博文为排列熵、模糊熵、近似熵、样本熵的原理及MATLAB实现”系列，关于排列熵、模糊熵的内容请阅读博客：

三、样本熵

1.简介

样本熵（Sample entropy，简称SampEn）是Richman等在2000年提出的一种新的时间序列复杂度表征参数。样本熵是在近似熵的基础上改进得到的，二者都是衡量时间序列的复杂性和维数变化时序列产生新模式概率的大小，产生新模式的概率越大，序列的复杂性程度越高，熵值就越大。与Lyapunov指数、信息熵、关联维数等其他非线性动力学方法相比，样本熵具有所需的数据短、抗噪和抗干扰能力强、在参数大取值范围内一致性好等优点，因而被广大学者所关注且近年来被常用于机械信号分析与故障诊断领域。

2.基本原理

设有长度为N的时间序列X={x(1)，x(2)，...，x(N)}，其样本熵的计算方法如下：

Step1:将时间序列X构造成m维矢量，即

Step2:定义X(i)与X(j)间的距离为d[X(i)，X(j)](i不等于j)，为两者对应元素中差值最大的一个，即

Step3:给定阈值r(r>0)，统计d[X(i)，X(j)]<r的数目并与总的矢量个数 N-m 的比值，即

Step4:对所有由式(3)得到的结果求平均，即：

Step5:再将维数 m 加 1，重复 Step1~ Step4。

Step6:则理论上此序列的样本熵为：

但实际中 N 不可能为无穷大，而为一有限值，则样本熵的估计值为：

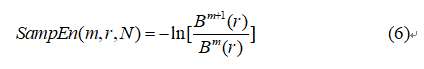
样本熵算法的优点：样本熵不包含自身数据段的比较，不仅提高了计算精度、节约了计算时间，而且也使得样本熵的计算不依赖数据长度；其次，样本熵具有更好的一致性，就是说如一序列比另一序列有较高的 SampEn，那么改变 m 和 r 值，也具有相对较高的 SampEn 值。总的来说，样本熵就是一种与近似熵相似但精度更好的方法。

3.MATLAB代码

%% 主函数
clc;
clear;
close all;

% 仿真信号
Fs=4000;   % 数据采样率
t=(0:1/Fs:(1-1/Fs))';
x=0.6*sin(500*pi*t+pi/4);

% 计算样本熵
dim=2;
r=0.2*std(x1);
sampEn = SampleEntropy( dim, r, x);

%% 样本熵函数
function sampEn = SampleEntropy( dim, r, data, tau )
%   注意：这个样本熵函数是在Kijoon Lee的基础上做的修改
%   样本熵算法的提出者：Richman J s，Moorman J R. Physiological time-seriesanalysis using approximate entropy and sample entropy[J. American Journal of Physiology Heart &. Circula-tory Physiology，2000，278(6):2039-2049.
%   计算给定时间序列数据的样本熵
%
%   样本熵在概念上类似于近似熵，但有以下区别：
%       1）样本熵不计算自匹配，通过在最后一步取对数，避免了可能出现的log(0)问题；
%       2）样本熵不像近似熵那样依赖数据的长度。
% 
%   dim：嵌入维数(一般取1或者2)
%   r：相似容限( 通常取0.1*Std(data)~0.25*Std(data) )
%   data：时间序列数据，data须为1xN的矩阵
%   tau：下采样延迟时间（在默认值为1的情况下，用户可以忽略此项）
% 
if nargin < 4, tau = 1; end
if tau > 1, data = downsample(data, tau); end

N = length(data);
result = zeros(1,2);

for m = dim:dim+1
    Bi = zeros(N-m+1,1);
    dataMat = zeros(N-m+1,m);
    
    % 设置数据矩阵，构造成m维的矢量
    for i = 1:N-m+1
        dataMat(i,:) = data(1,i:i+m-1);
    end
    
    % 利用距离计算相似模式数
    for j = 1:N-m+1
        % 计算切比雪夫距离，不包括自匹配情况
        dist = max(abs(dataMat - repmat(dataMat(j,:),N-m+1,1)),[],2);
        % 统计dist小于等于r的数目
        D = (dist <= r);
        % 不包括自匹配情况
        Bi(j,1) = (sum(D)-1)/(N-m);
    end
 
    % 求所有Bi的均值
    result(m-dim+1) = sum(Bi)/(N-m+1);
	
end
    % 计算得到的样本熵值
    sampEn = -log(result(2)/result(1));
	
end

实例分析：

4.参考文献

[1]样本熵理论相关知识与代码实现

[2]郑近德，陈敏均，程军圣，等. 多尺度模糊熵及其在滚动轴承故障诊断中的应用[J]. 振动工程学报，2014,27（1）：1145-151.

[3]来凌红，吴虎胜，吕建新，等. 基于ＥＭＤ和样本熵的滚动轴承故障SVM识别[J]. 煤矿机械，2011，32（1）：249-252.