LeetCode高频面试60天打卡日记Day10

Day10

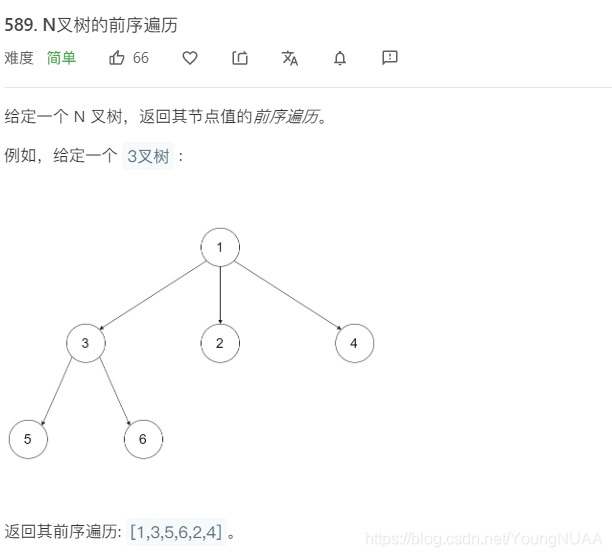
递归：
/*
// Definition for a Node.
class Node {
    public int val;
    public List<Node> children;

    public Node() {}

    public Node(int _val) {
        val = _val;
    }

    public Node(int _val, List<Node> _children) {
        val = _val;
        children = _children;
    }
};
*/
//前序遍历
class Solution {
    
    
    List<Integer> NodeList = new LinkedList<>();
    public List<Integer> preorder(Node root) {
    
    
        if(root==null){
    
    
            return NodeList;
        }

        NodeList.add(root.val);
        for(Node child:root.children){
    
    
            preorder(child);
        }
        return NodeList;
    }
}

//后序遍历
class Solution {
    
    
    List<Integer> ans = new LinkedList<Integer>();
    public List<Integer> postorder(Node root) {
    
    
        if(root == null){
    
    
            return ans;
        }
        for(Node child:root.children){
    
    
            postorder(child);
        }
        ans.add(root.val);
        return ans;
    }
}

//非递归--前序遍历
class Solution {
    
    
    public List<Integer> preorder(Node root) {
    
    
 		List<Integer> stack = new LinkedList<>();
        List<Integer> output = new LinkedList<>();
        if(root == null){
    
    
            return output;
        }
        
        stack.add(root.val);
        while(!stack.isEmpty()){
    
    
            Node node = stack.pollLast();
            output.add(node.val);
            Collections.reverse(noed.children);
           	for(Node temp:node.children){
    
    
                stack.add(temp);
            }
        }
        return output;
    }
}

解析：

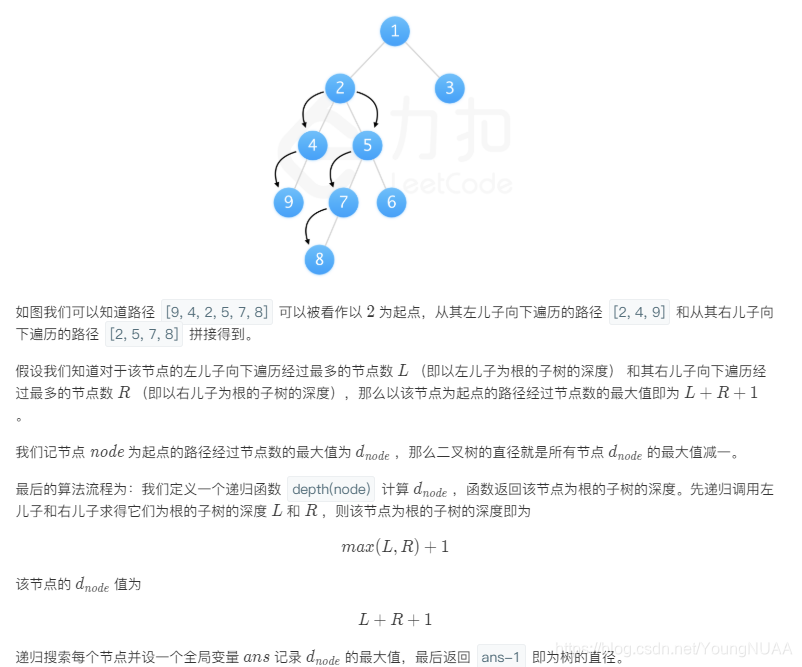
class Solution {
    
    
    int ans;
    public int diameterOfBinaryTree(TreeNode root) {
    
    
        ans = 1;
        depth(root);
        return ans - 1;
    }
    public int depth(TreeNode node) {
    
    
        if (node == null) return 0; // 访问到空节点了，返回0
        int L = depth(node.left); // 左儿子为根的子树的深度
        int R = depth(node.right); // 右儿子为根的子树的深度
        ans = Math.max(ans, L+R+1); // 计算d_node即L+R+1 并更新ans
        return Math.max(L, R) + 1; // 返回该节点为根的子树的深度
    }
}