本文的灵感其实是来自男厕,但是为了文明起见,文明还是换成安排座位的场景吧,正好疫情期间大家对电影院隔位安排座位应该也有感觉。
隔位公理一:在使用座位的时候,我们都不愿意和别人相邻,否则太尴尬了。
隔位公理二:每个人都愿意离其他人尽量远。
那么问题来了,这样的限制下,会发生怎样的玄学故事呢?
一,统一安排座位的场景
如果是统一安排,那么问题就很简单。
假设所有的座位是n个座位排成一排,那么最极端的2个场景就是内固场景和外固场景。
1,内固场景
最多可以安排多少个座位,使得两两不相邻?
答案是n/2,任何俩人之间的距离都是2,即俩人之间有且仅有一个座位。
2,外固场景
最少需要安排多少个座位,使得再也无法安排新的座位?
答案是n/3,任何俩人之间的距离都是3
二,各自加入的场景
如果所有人都先后使用座位,没有任何俩人是同时使用,不考虑使用结束的情况(一直使用)
那么,会出现什么情况呢?
我们用0代表没有人的空位,用1代表有人的位置。
1,6座位场景
刚开始是000000,随着人数增加,就会有几种情况:
(1)000100,010100,010101,结束
(2)000010,100010,101010,结束
(3)000001,100001,100101,结束
PS:假设在对称的情况下,选靠右的,因为进出厕所都要从右边走。
2,座位残缺场景
最近3号位置貌似堵了还是怎么的,用不了了,开局是000-00于是就会有这么几种情况:
(1)100-00,100-01,101-01,结束
(2)010-00,010-01,结束
(3)001-00,001-01,101-01,结束
(4)000-10,100-10,101-10,结束
(5)000-01,100-01,101-01,结束
3,第一人随机的场景
策略已经很清晰了,第一个人可以随机选择一个位置,后面的每个人都会选择离其他人最远的位置。
这是一个贪心的选择方案,每次选择时只需要根据当前局面做出最好的选择即可。
注意,在类似0100001这种情况下,局面并不对称,会有0101001和0100101两种选择,所有当n比较大的时候会有很多选择,并不是第一个人的选择就能决定最终局面。
那么问题来了,n个座位平均情况下可以让多少人使用呢?
首先考虑一个确定性问题:如果第一个人选择最靠边的位置,那么最多能有多少人?
假设这个问题的答案是f(n),那么有递推式f(n)=f(n/2+1)+f(n-n/2)-1
把n从2到99时,f(n)的值列举出来:
#include<iostream>
using namespace std;
int main()
{
int a[100];
a[2] = 1, a[3] = 2;
cout << "1 2 ";
for (int i = 4; i < 100; i++) cout << (a[i] = a[i / 2 + 1] + a[i - i / 2] - 1)<<" ";
return 0;
}1 2 2 3 3 3 4 5 5 5 5 5 6 7 8 9 9 9 9 9 9 9 9 9 10 11 12 13 14 15 16 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17 17
18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33 33
33 33 33 33 33 33 33 33 34 35
规律非常明显:
(1)是递增数列
(2)包含所有正整数
(3)1出现1次,2出现2次,3出现3次,5出现5次,9出现9次,17出现17次......其他的数恰好出现1次。
于是我们可以给出f(n)的表达式:
f(1)=1,f(2)=2,f(3)=2,当k>3时:

其中第(1)种情况中的f(n)的值都是数列中只出现一次的数,第(2)种情况中的f(n)的值都是数列中连续出现f(n)次的数。
比如k=2, 12<n<=24时
(1)12<n<=15, f(n)=n-7, 即6,7,8分别出现1次
(2)16<=n<=24, f(n)=9,即9出现9次
根据f的表达式我们也可以看出,f(n)/n是一个震荡型函数,没有极限,它有无穷个极大值和无穷个极小值,极大值是依次递减,趋向1/2,极小值是依次递减,趋向1/3
回到原问题,n个座位平均情况下可以让多少人使用呢?
第一个人在n个座位里面随机选一个,所以均值是

这个式子也可以根据f(n)的表达式算出分段的表达式。
4,全员随机的场景
如果只保留公理一,去掉公理二,也就是说,所有人都随机选择位置,最后的外固场景会是什么样呢?
假设均值是g(n),则n/3 <= g(n) <= (n+1)/2,实际上每种情况下最后的座位使用数量都在这个范围内。
和上面类似的,我们可以得到g(n)的递推式:
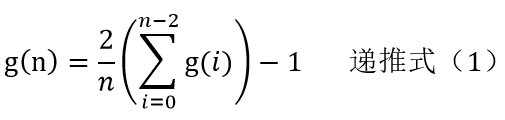
用我们高中熟知的方法进行化简得到递推式(2) g(n+1)=(ng(n)+2g(n-1)+1)/(n+1),这是一个二阶非线性递推公式。
g(0)=0,g(1)=1,g(2)=1,g(3)=5/3......
递推式(1)的这个形式难免让我们想起施笃兹定理,不过很可惜,并不能证明g(n)/n有极限,甚至我怀疑这和f(n)/n一样是震荡型函数。