堆应用(动态数据求top k,动态数据求中位数)
动态数据集合中求top k大元素
第1大,第2大 ...第k大 k是这群体里最小的 所以要建立个小顶堆 只需要维护一个大小为k的小顶堆 即可 当来的元素(newCome)> 堆顶元素(smallTop),说明进来的元素有和堆顶竞争的资格,此时的堆顶被踢出 这时把进来的元素放到堆顶 newCome>smallTop,smallTop的左右孩子>smallTop,所以无法确认 newCome和smallTop的左右孩子的大小关系, 在newCome和smallTop的左右子节点找到最小的元素和newCome交换,然后继续比较newCome与被交换的左右孩子的大小关系 持续这个过程(堆化)即可
如果每次询问前K大数据,我们都基于当前的数据重新计算的话,那时间复杂度就是O(nlogK),n表示当前的数据的大小
部分代码
topn.php
$static_data=[2,5,3,1,0,7,6,10];
//第3大
/*
2,5,3 2
2,5,3 1 2
2,5,3,1,0 2
2,5,3,1,0,7 3
2,5,3,1,0,7,6 5
2,5,3,1,0,7,6,10 6
维持1个小顶堆 大小为3即可
*/
$heap=new Heap(3); //建立一个大小为3的小顶堆
foreach ($static_data as $v){
echo $heap->topn($v).PHP_EOL;
}
heap.php
public function topn($data)
{
//堆满了
if ($this->isFull()) {
if ($data > $this->dataArr[1]) {
$this->dataArr[1] = $data;
$this->smallHeapFirst();
}
} else {
$this->dataArr[$this->count + 1] = $data;
$this->count++;
$this->smallHeapLast();
}
return $this->dataArr[1];
}
动态数据流求中位数
2,3,1,7,5 返回3 1,3,1,7,5,4 返回3,4 数据持续往里面进,每进来一个数,就询问中位数是谁们
step1 思路分析:
所谓中位数,就是中间大的1个或者2个元素,中位数满足的性质,中位数之前的数都它,之后的数都大于它 先以奇数个分析,偶数个原理一样 1.如果是固定的数据集合,比如数据为n个,中位数即为n/2+1 大的元素,此时只需维护一个大小为(n/2+1) 大小的小顶堆即可 为什么不能是大顶堆呢,如果堆顶最大,除了知能找到这群集合的最大值外,其它的都无从知晓了 如果是小顶堆,堆顶最小,数据集合比如为5个,第3大的元素肯定小于已经比较过的前2个数,即为中间元素 但是现在是动态数据流,每次进来1个元素,都会询问中间元素 和静态数据的区别是:不知道维护的小顶堆的大小了 这时需要维护2个堆了,来了数据,分别放到这2个堆 1个大顶堆,1个小顶堆,大顶堆的数据均小于小顶堆的数据,当要询问的时候 如果是偶数个数据,两个堆的堆顶元素即为中间元素 如果奇数个数据,两个堆中数据较多的那个堆的堆顶元素即为中间元素
step1 步骤分析
大顶堆为big,堆顶元素bigpeak,大小为bigsize,小顶堆称small,堆顶元素为smallpeak,大小为smallsize 进来1个元素,big为空 :放入big big不为空: 放入元素<bigpeak,放入到big 放入元素>bigpeak, 放入到small 放入1个元素完成后 如果bigsize-smallsize>1,把big元素的堆顶元素拿掉 堆化big,把拿掉的元素放入small 然后堆化 如果bigsize-smallsize<1,把small元素的堆顶元素拿掉 堆化small,把拿掉的元素放入big 然后堆化
findmiddle.php
$arr = [9, 8, 11, 4, 2, 6, 5, 1, -1, 3, 20, 10];
//$arr=[9,8,11,4,2,6,5,100];
findMiddle($arr);
//动态数据实时获取中位数
function findMiddle($arr)
{
//大顶堆
$bigHeap = new Heap(0, 1);
//小顶堆
$smallHeap = new Heap(0, 0);
foreach ($arr as $k => $v) {
if ($bigHeap->isEmpty()) {
$bigHeap->insert($v);
} else {
$bigPeak = $bigHeap->peak();
if ($v < $bigPeak) {
$bigHeap->insert($v);
} else {
$smallHeap->insert($v);
}
if ($bigHeap->count - $smallHeap->count > 1) {
$bigPeak = $bigHeap->deleteFirst();
$smallHeap->insert($bigPeak);
} elseif ($smallHeap->count - $bigHeap->count > 1) {
$smallPeak = $smallHeap->deleteFirst();
$bigHeap->insert($smallPeak);
}
}
//实时获取中位数
echo implode(',', midPeak($bigHeap, $smallHeap)) . PHP_EOL;
}
}
function midPeak($heap1, $heap2)
{
if ($heap1->count == $heap2->count) {
$midArr = [$heap1->peak(), $heap2->peak()];
} elseif ($heap2->count > $heap1->count) {
$midArr = [$heap2->peak()];
} else {
$midArr = [$heap1->peak()];
}
return $midArr;
}
过程分析
几个重要的点
- 两个堆元素数相等时中间元素为两个堆顶
否者为较多元素堆的堆顶 - 两者元素个数差值大于1时,要调整堆的元素个数
依次插入的元素 为 9, 8, 11, 4, 2, 6, 5, 1, -1, 3, 20, 10,大顶堆 称为big,小顶堆称为small,各自大小bigsize,smallsize,堆顶为bigpeak,smallpeak, 9进来 big为空,插入big, bigsize-smallsize=1 不大于1 此时bigsize>smallsize 中间元素为bigpeak即为[9] 8进来 8<bigpeak, 插入big,bigsize-smallsize=2 大于1 此时bigpeak 需要从Big删除,big堆化,放入到small ,small堆化 ,此时bigsize=smallsize 所以中间元素为[bigpeak,smallpeak] 即为[8,9] 11进来 11>bigpeak(8),11插入small,此时smallsize=2,bigsize=1,差值不大于1,因为smallsize>bigsize,中间元素为[smallpeak] 即为[9] 4进来 4<bigpeak(8),4插入到big,big堆化,此时bigsize=2,smallsize=2,中间元素为[bigpeak,smallpeak] 即为[8,9]
此时堆图
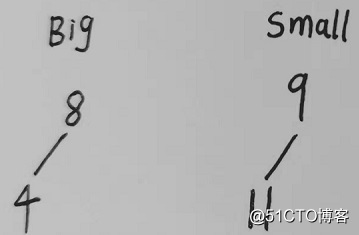
2进来 2<8 ,2插入big然后堆化,bigsize=3,smallsize=2 所以此时中位数为[8] 6进来 6<8,6插入big后堆化 为下图
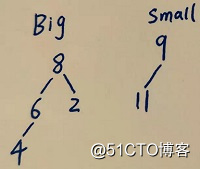
此时,bigsize=4,smallsize=2,bigsize-smallsize>1,删除big的堆顶元素 堆化,然后把把删除的元素插入到small,堆化后 此时big,small见下图,中间元素位[bigpeak,smallpeak]即 [6,8]
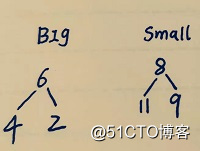
5进来 5<bigpeak(8),5插入big堆化 此时Bigsize=4,smallsize=3,差值不大于1,中间元素位bigpeak 即为[6] 之后的步骤同理
插入数据因为需要涉及堆化,所以时间复杂度变成了O(logn),但是求中位数我们只需要返回大顶堆的堆顶元素就可以了,所以时间复杂度就是O(1)
扫描二维码关注公众号,回复:
13040931 查看本文章

