近年来,随着人口的快速增长,群体计数在视频监控、交通管制和体育赛事等方面得到了广泛应用。早期的研究工作通过检测身体或头部来估计人群数量,而其他一些方法则学习从局部或全局的特征到实际数量的映射关系来估计数量。最近,群体计数问题被公式化为人群密度图的回归,然后通过对密度图的值进行求和以得到图像中人群的数量。随着深度学习技术的成功,研究人员采用卷积神经网络(CNN)生成准确的群体密度图,并能获得比传统方法更好的表现。
然而,由于尺度变化(scale variation)较大、遮挡严重、背景噪声和透视失真,群体计数仍然是一项极具挑战性的任务。其中,尺度变化是最主要的问题。为了更好地处理尺度变化,研究人员提出了许多多列(multi-column)或多分支(multi-branch)网络。这些架构一般由 CNN 的几个列或主干网络不同阶段的几个分支组成。这些列或分支具有不同的感受野,以感知人群大小的变化。尽管这些方法有了很好的改进,但它们捕获的尺度多样性受到列或分支数的限制。
尺度变化的主要挑战在于两个方面。首先,如图 1 左所示,人群图像中的人通常大小不同,从几个像素到几十个像素不等。这就要求网络能够处理尺度变化很大的数据。第二,如图 1 右所示,整个图像的尺度通常连续变化,特别是对于高密度图像。这就要求网络能够对尺度范围进行密集采样。然而,现有的方法并不能同时应对这两个挑战。

图 1 群体计数数据集中存在较大的尺度变化。左:Shanghai Tech 中输入图像和对应的真实密度图。右:UCF-QNRF 数据集中输入图像和对应的真实密度图。
本文提出了一种新的密集尺度单栏神经网络——DSNet,用于群体计数。DSNET 由密集连接的扩张卷积块组成,因此它可以输出具有不同感受野的特征,并且捕获不同尺度的人群信息。DSNet 的卷积块与 DenseASPP 结构相似,但具有不同的扩张率组合。作者为块内的层仔细选择这些比率,这样每个块对连续变化的尺度进行更密集的采样。同时,所选择的扩张率组合可以利用感受野的所有像素进行特征计算,防止网格化效果。为了进一步提高 DSNet 捕获的尺度多样性,作者堆叠了三个密集扩张卷积块,并利用残差连接(residual connection)进行密集连接。最终的网络能够以更密集的方式对非常大的尺度变化范围进行采样,从而能够处理群体计数中尺度变化较大的问题。
以前大多数方法使用传统的欧几里德损失(Euclidean loss)训练网络,这是基于像素独立性的假设。这种损失忽略了密度图的全局和局部一致性,会影响群体计数的结果。为了解决这一问题,作者提出了多尺度密度水平一致性损失,用于保证估计的人群密度图和真实人群密度图之间的全局和局部的密度水平保持一致。
论文贡献
提出了密集扩张卷积块(DDCB),其扩张率是仔细选择的。DDCB 能够对连续变化的尺度进行密集采样。DSNet 可以进行端到端的训练,并且可以处理拥挤和稀疏的人群图像。
引入了多尺度密度水平一致性损失,以提高模型表现。该损失加强了估测密度图和真实密度图之间的全局和局部一致性。
作者在四个具有挑战性的公开群体统计数据集上进行了广泛的实验。与现有的最先进方法相比,该方法获得了最佳性能。在 UCF-QNRF 和 UCF_CC_50 数据集上的计数准确率提高了 30%,在 Shanghai Tech 和 UCSD 数据集上的计数准确率提高了 20%。
2 DSNet
该方法基本思想是一个端到端的单列 CNN,具有更密集的尺度多样性,以应对密集和稀疏场景中的大的尺度变化和密度水平差异。DSNET 的体系结构如图 2 所示。

图 2 DSNet 网络结构。DSNet 由 VGG-16 网络的前十层组成的主干网、三个具有密集残差连接(DRC)的密集扩张卷积块(DDCB)和三个用于人群密度图回归的卷积层组成。利用带 DRC 的 DDCB 来扩大特征的尺度多样性和感受野,以应对较大的尺度变化,从而准确估计密度图。
2.1 DSNet 结构我们提出的 DSNET 包含主干网络作为特征提取器,三个密集的扩张卷积块,由密集残差连接堆叠,扩大了尺度多样性,以及三个卷积层,用于人群密度图回归。
主干网络
本文所用的主干网络为 VGG-16 的前十层,以及三个池化层。经验表明,在多列网络中,使用内核较小但层数较多的卷积层比内核更大但层数更少的卷积层更有效。此外,它还实现了准确率与计算量之间的最佳权衡,适用于准确、快速的人群计数。
密集扩张卷积块(Dense dilated convolution block,DDCB)
为了应对尺度变化的挑战,需要一种能够以尽可能密集的方式捕获大范围尺度变化的网络架构。本文提出了一种新的密集扩张卷积块,它包含三个扩张卷积层,其扩张率为 1,2,3。这种设置可以保留来自更密集尺度的信息,并且感受野尺寸差距较小。区块内的每个扩张层与其他层紧密相连,因此每个层都可以访问所有后续层,并传递需要保留的信息。密集连接后,获得的尺度多样性增加,如图 3 所示。
图 3 DDCB 尺度多样性与密集堆叠的扩张卷积中扩张率(1,2,3)的设置相对应。k 表示相应组合的感受野大小。
精心选择膨胀率的另一个优点是,它可以克服网格化效果。如图 4 所示,扩张率为 6 的扩胀卷积层位于扩张率为 3 的扩张卷积层下方。在一维情况下,经过这两层之后,一个像素的最终结果只能从 7 个像素中获得信息。当输入数据是二维时,这种现象会变得更糟。因此,最终像素只能以网格方式查看原始信息,并丢失大部分(86.4%)信息。由于原始特征图的局部信息完全丢失,并且由于扩张率大,信息在大距离内可能不相关,这不利于群体计数中捕获详细特征。通过采用新的扩张率组合,顶层可以覆盖原始特征图的所有像素信息,避免中间层扩张率过大造成的大距离无关信息。这对于人群计数的准确性至关重要。
图 4(a)在 DenseASPP 中具有较大膨胀率的叠加膨胀卷积层,导致“网格化效果”,丢失大量信息。红色表示信息的来源。(b)本文所提出的 DDCB 中具有(1,2,3)膨胀率的后续卷积层,以覆盖所有的像素信息。
密集残差连接(Dense residual connection,DRC)虽然 DDCB 提供了密集尺度多样性,但不同块之间的层次特征没有得到充分利用。因此,作者通过密集的残差连接来改进体系结构,以进一步改进信息流。此外,与传统的密集连接相比,它们还可以防止网络变得更宽。这样,DDCB 的输出可以直接访问后续 DDCB 的每一层,从而实现连续的信息传递。与普通的残差连接相比,进一步扩大了尺度多样性,并在信息流过程中自适应地保留了适合特定场景的特征。
2.2 损失函数
以往的研究大多使用欧几里得距离损失作为群体计数的损失函数,它只考虑像素误差,而忽略了估计密度图和真实密度图之间的全局和局部相关性。在本文中,作者将多尺度密度水平一致性损失与欧几里得损失结合起来,衡量全局和局部的一致性。
欧几里得损失
欧几里得距离用于测量估计密度图与真实值之间像素级的估计误差。损失函数定义如下:
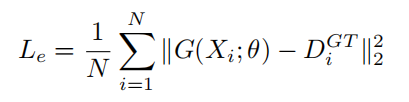
其中 N 是一个 batch 中图像的数目,G(Xi;θ) 是训练图像 Xi 的估测密度图,参数为θ。D 是 Xi 的实际密度图。
多尺度密度水平一致性损失除了像素级损失函数外,作者还考虑了估计密度图和真实值之间的全局和局部密度水平一致性。新提出的训练损失定义为:
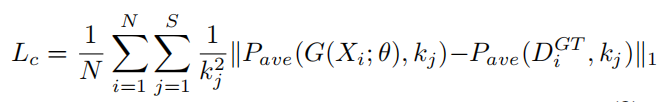
其中 s 是用于一致性检查的尺度级别数,P 是平均池化操作,kj 为平均池化的指定输出大小。
尺度级别将密度图分割成不同的子区域,并形成池化表示,说明不同位置的人群密度级别。根据密度水平的上下文,在不同的尺度上,估计的密度图需要与实际情况保持一致。此外,尺度级别的数量和特定尺度的输出尺寸控制着训练速度和估计精度之间的权衡。作者采用三个尺度级别,每个输出尺寸分别为 1×1、2×2 和 4×4。输出大小为 1×1 的第一个尺度级别捕获密度水平的全局特征,而其他两个尺度级别表示图像块的局部密度水平。
最终目标函数
通过对上述两个损失函数加权求和,整个网络使用以下目标函数进行训练:
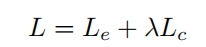
其中λ是平衡像素和密度水平一致性损失的权重。实验中,不同数据集λ的设定值如表 1 所示。
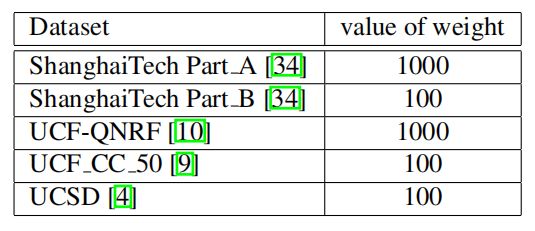
表 1 不同数据集的λ值
3 实现 3.1 生成真实值对于数据集中密集人群的场景图,采用几何自适应核处理生成密度图,而对于数据集中人群相对稀疏的图像,采用固定高斯核生成密度图。
3.2 评价方法在测试时,将整个图像输入网络以生成估计的密度图。采用平均绝对误差(MAE)和均方误差(MSE)来评价网络性能。MAE 反映了模型的准确性,而 MSE 则反映了模型的鲁棒性。数值越低则意味着更好的表现。这两个指标定义如下: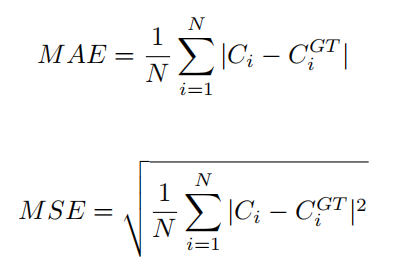
其中 n 是测试集中的图像数,Ci 表示预测计数,而 Cgti 表示真实计数值。
4 实验 4.1 数据集论文在四个可用的群体统计数据集上评估了 DSNet:ShanghaiTech、UCF-QNRF、UCF_CC _50 和 UCSD。
ShanghaiTech: 包含标注图片 1198 张,共 330165 人,分为 A 和 B 两个部分,A 包含 482 张图片,均为网络下载的含高度拥挤人群的场景图片,人群数量从 33 到 3139 个不等,训练集包含 300 张图片和测试集包含 182 张图片。B 包含 716 张图片,这些图片的人流场景相对稀疏,拍摄于街道的固定摄像头,群体数量从 12 到 578 不等。训练集包含 400 张图像,测试集包含 316 张图像。
UCF-QNRF: 这是最新发布的最大人群数据集。它包含 1535 张来自 Flickr、网络搜索和 Hajj 片段的密集人群图像。数据集包含广泛的场景,拥有丰富的视角、照明变化和密度多样性,计数范围从 49 到 12865 不等,这使该数据库更加困难和现实。此外,图像分辨率也很大,因此导致头部尺寸出现大幅变化。
UCF_CC_50: 包括 50 张黑白低分辨率图像,人流场景非常密集。每张图片的标注人数从 94 人到 4543 人不等,平均人数为 1280 人,这使得深度学习的方法具有挑战性。
UCSD: 由 2000 帧监控摄像机拍摄的照片组成,尺寸为 238×158。这个数据集的密度相对较低,每幅图像 11 到 46 人不等,平均约 25 人。在所有帧中,帧 601 到 1400 为训练集,其余帧为测试集。
4.2 对比实验作者在四个具有挑战性的公开群体计数数据集上进行了对比实验。实验结果见表 2。可以看出,论文提出的方法在所有数据集和所有评估指标上都达到了最先进的性能。说明所提的方法不仅适用于拥挤的人群场景,也适用于稀疏的人群场景。
表 2 与 Shanghai Tech、UCF-QNRF、UCF_CC_50 和 UCSD 数据集上的最新方法进行比较。与当前最先进的方法相比,DSNet 获得最佳性能,并且具有大幅提升。
该方法的几个密度图示例如图 5 所示。很明显,DSNet 取得了较好的表现。图 5 还验证了该方法可以捕获不同大小的头部尺寸,从而使 DSNet 更加鲁棒和准确。
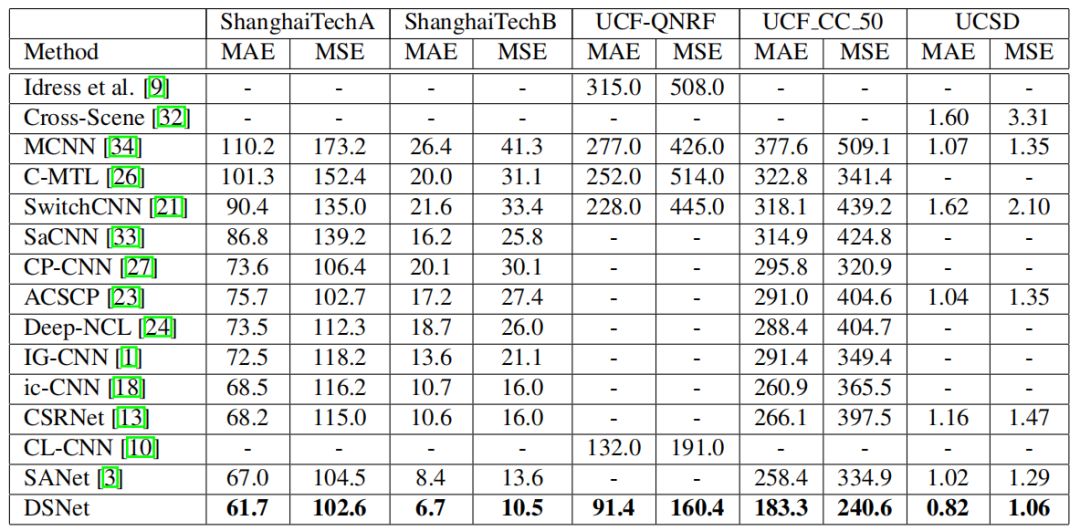
图 5 由 DSNet 生成的估计密度图和人群数量的图示。第一行为从 ShanghaiTech A、ShanghaiTech B 和 UCF-QNRF 数据集中提取的四个样本。第二行显示 DSNet 估计的密度图。最后一行显示了相应的真实密度图。DSNet 能够生成接近真实情况的密度图和精确的人群计数。
4.3 消融实验在本节中,作者在 ShanghaiTech B 数据集上进行了消融实验,分析了网络构成和损失函数。
网络结构: DSNet 包括主干网络、密集扩张卷积块、密集残差连接和多尺度密度级一致性损失。为了证明它们的有效性,作者通过增加这些组件来进行实验。实验结果见表 3。
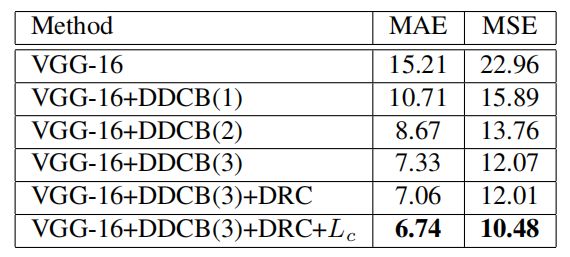
表 3 在 Shanghai Tech B 数据集上,网络的不同组件的估计误差。括号中的数字是密集扩张卷积块的数目。
作者使用后端网络和最后三个卷积层作为基线模型,MAE 值为 15.21,这是表中所有项目中最低的,但仍然可以比过大多数现有方法。仅通过增加所提出的 DDCB,MAE 降低到 7.33,与以往的方法相比有较大幅度的提高,达到了最佳的性能。说明了密集扩张卷积块所产生的尺度密集、感受野大的特征,对于准确、可靠地计算群体数量是必不可少的。
此外,在三个密集扩张卷积块之间增加密集残差连接也改善了结果,MAE 进一步降低到 7.06,这表明密集残差连接通过重复利用不同 DDCB 的特征进一步扩大了尺度多样性。
最后,增加密度级一致性损失来训练整个网络。它进一步将平均绝对误差降低到 6.74,这是所提出方法的最佳性能,并在数据集上达到了最先进的水平。结果表明,该损失可以使估计密度图的密度水平与真实值的密度水平在全局和局部上相一致。
此外,作者比较了密集残差连接与普通残差连接的影响。实验结果见表 4。通过利用残差连接,估计的误差减小到 6.81,这是由于前一个块的特征得到重用,而忽略了其他具有不同尺度的块的特征。为了解决这一问题,采用密集的残差连接进一步将 MAE 降低到 6.74,这表明尺度多样性进一步扩大,特征更加有效。
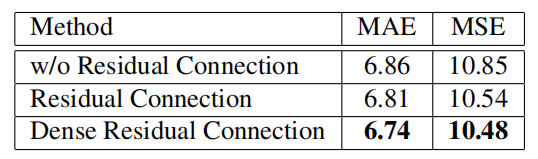
表 4 不同残差连接的估计误差。
损失函数: 作者提出的新损失采用三个尺度(即平均池化操作的 1×1、2×2、4×4 输出大小)。作者对这三个尺度级别进行了实验,证明每一个尺度级别都能使估计的密度图与真实值之间的一致性得到规范。实验结果见表 5。
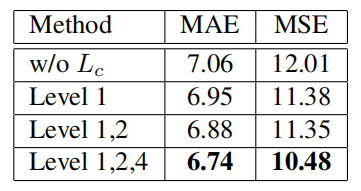
表 5 所提出的一致性损失在不同尺度级别的估计误差。数字为平均池化操作的输出大小。
在加入一致性损失函数之前,该网络的 MAE 值达到了 7.06。采用输出尺寸为 1×1 的单尺度级别,即整个输入图像密度水平的全局上下文,平均绝对误差减小到 6.95。此外,由于加入输出尺寸为 2×2 和 4×4 的局部密度水平的约束,性能继续得到改善,使 MAE 分别降低到 6.88 和 6.74。这些增量实验表明,密度水平的全局和局部正则化都有助于约束估计的密度图与不同尺度上的真实密度图相一致,从而生成高质量的密度图。
5 结论
本文提出了一种新的端到端的单列模型 DSNet,该模型基于具有密集残差连接的密集扩张卷积块,能够准确估计群体数量。这两个组成部分扩大了尺度的多样性和特征的感受野,可以解决尺度变化较大的问题,从而在统计图像群体数量问题取得了良好的表现。此外,本文引入了一种新的损失来加强估计密度图的密度水平,使其在不同尺度上与相应的真实值相一致。该方法在四个具有挑战性的公开群体计数数据集上取得了最先进的结果,并相比以前的方法有大幅提升。