[第一章——函数、极限、连续]
[第二章——导数与微分]
[第三章——微分中值定理及导数应用]
【复习多元的思路】
学习多元,需要同一元进行对照学习,主要抓住两点
一:哪些是相同点
二:哪些是不同点
本章节对应一元函数微分学中的一、二、三章

第一节 多元函数的基本概念
主要复习四个重要概念:重极限、连续、偏导数、全微分
对应着一元函数微分学中的四个重要概念:极限、连续、导数、微分
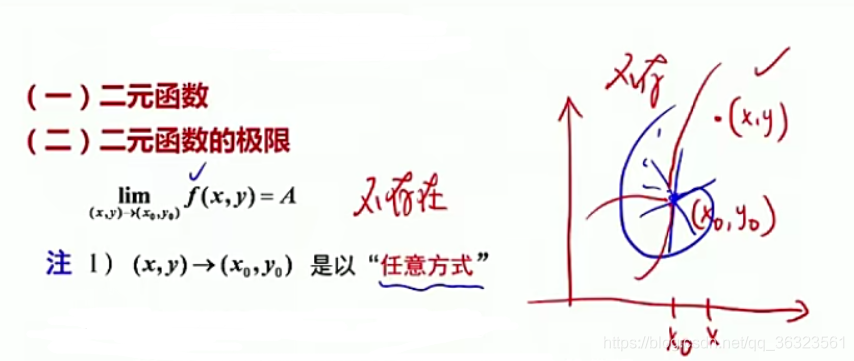
8.1.1 多元函数的极限
即重极限,对应一元函数微分学中的极限
研究多元,通常以二元为例,一元到二元通常有本质性的变化,二元到三元及以上,没有本质性的变化
自变量存在于平面上的二维空间,动点趋向于定点的方式比一元的方式复杂得多
【notes】
一元函数极限中的下述性质对多元函数仍成立
① 局部有界限
② 保号性
③ 有理运算
④ 极限与无穷小的关系
⑤ 夹逼性d
【求极限】
多元求极限一般只有三种情况
高阶/低阶,一般为0;
同阶/同阶,一般为无穷;
低阶/高阶,一般极限不存在
【极限存在求极限】
多元求极限时,第一步往往是判断极限的存在性
本题为高阶/低阶,可知极限为0,故设法证明极限为0即可
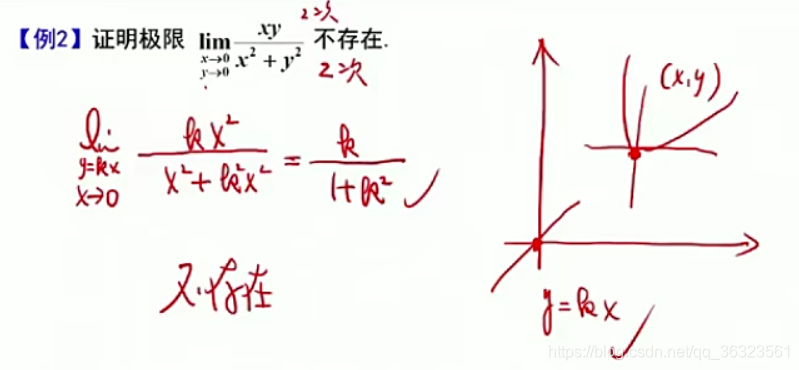
【证明极限不存在】
当分子分母同次是,一般极限不存在。而证明极限不存在的方法一般是找不同路径上的两个极限值不同来说明(或是存在任意一个路径上的极限不存在也可说明)
8.1.2 多元函数的连续性
对应一元函数微分学中的连续性
8.1.3 偏导数
对应一元函数微分学中的导数
8.1.4 全微分
对应一元函数微分学中的微分
8.1.5 连续、可导、可微之间的关系
第二节 多元函数的微分法
8.2.1 复合函数微分法
8.2.2 隐函数为微分法
第三节 多元函数的极值与最值
一元函数微分学中,有微分中值定理以及倒数的应用,而在多元函数微分学中,没有微分中值定理
在一元中,有了微分中值定理,可以用导数研究极限,从而有了洛必达,而在多元中,没有洛必达
在一元中,导数可以研究函数的增减性。而多元中,函数就没有定义过增减性,这个问题就没有
一元可以用导数来研究函数的极值和最值,多元也有这个问题
一元可以研究函数曲线的凹凸性,多元在考研阶段不做研究