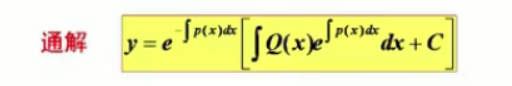第七章_常微分方程

$\partial z$

【考试内容概要】

常微分方程的基本概念
一阶微分方程
可降阶的高阶方程
高阶线性微分方程

【常考题型与典型例题】

题型一 微分方程求解
题型二 综合题
题型三 应用题

7.1 常微分方程的基本概念

1、微分方程
2、微分方程的阶
3、微分方程的解
4、微分方程的通解
5、微分方程的特解
6、初始条件
7、积分曲线

1、微分方程

  含有未知函数的导数或微分的方程称为 微分方程，简称 方程。

2、微分方程的阶

  微分方程中所出现的未知函数最高阶导数的阶数，称为微分方程的 阶。

3、微分方程的解

  满足微分方程的函数，称为该方程的 解。

4、微分方程的通解

  如果微分方程的解中含有任意常数，且任意常数的个数与微分方程的阶数相同，则称之为微分方程的 通解。

如一阶微分方程，通解有一个任意常数
如二阶微分方程，通解有两个任意常数

5、微分方程的特解

  微分方程的不含任意常数的解，称之为 特解。

当微分方程的通解中的任意常数被确定后，则得到微分方程的一个特解。

6、初始条件

  确定特解的一组常数称为 初始条件。

【无关内容】

物理学中运动的东西往往可以用微分方程来表示，那么这种运动的状态往往和它初始的状态是密切相关的，所以数学上将这样的条件称为初始条件

7、积分曲线

  方程的一个解在平面上对应一条曲线，称为该微分方程的 积分曲线。

7.2 一阶微分方程

主要考察前三类，后两类在试卷中出题频率很低

一阶微分方程形如：$y^{\prime }=f(x,y)$

7.2.1 可分离变量的方程

若一阶微分方程中，$f(x,y)$可拆开为$f(x)\cdot g(y)$，则称之为 可分离变量的方程。

【求解方法】

s1、分离变量
s2、两边 积分

7.2.2 齐次微分方程

这里的“齐次”和代数里面所讲的齐次非齐次方程组，同字不同含义，后者者讲的是非齐次项是否为零

若一阶微分方程能化为 $\frac{dy}{dx}=\varphi (\frac{y}{x})$ 的形式，则称其为 齐次微分方程。

【求解方法】

s1：做变量代换
s2：化成可分离变量型
s3：求解

7.2.3 一阶线性微分方程

$y^{\prime }+p(x)y=Q(x)$

线性：线性是针对未知函数y而言的，y与y’都是一次的，$p(x)$与$Q(x)$可以是任意形式

【求解方式】

公式直接代

这里求积分时，不用加绝对值

【公式由来】

公式来源于常数变易法
当Q(x)为零时，变为变量可分离型，此时可找出通解，即对应的齐次方程的通解项。

7.2.4 伯努利方程

  形如 $y^{\prime }+p(x)=Q(x)\cdot y^{\alpha }$ 的方程（$n\ne 0,1$），称为伯努利方程

伯努利方程相对于一阶线性微分方程，有一个 $y^{\alpha }$

【求解思路】

因为伯努利方程与一阶线性微分方程类似，所以解题思路是伯努利方程化为一阶线性微分方程

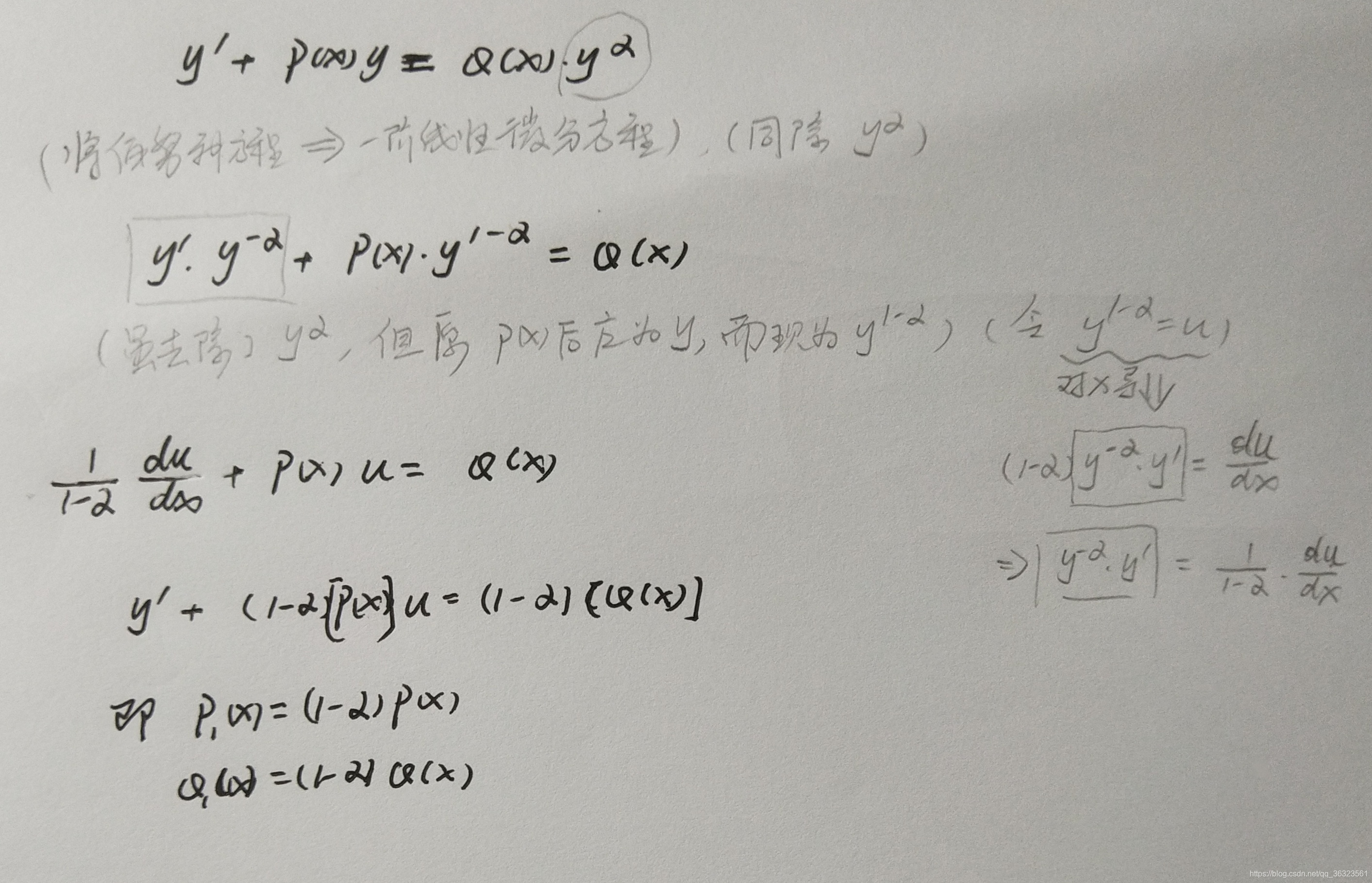
7.2.5 全微分方程

  如果方程
$$P(x,y)dx+Q(x,y)dy=0$$
的左端是某个函数 $u(x,y)$ 的全微分，即：
$$du(x,y)=P(x,y)dx+Q(x,y)dy$$
，则称该方程为 全微分方程.

【处理方法】

1、判定：
  若满足 $\frac{\nabla P}{\nabla y}=\frac{\nabla Q}{\nabla x}$，即两个偏导数相等

2、解法：（有三种）

偏积分	凑微分	线积分

上述三种方法都是多元微分中所学的方法

7.3 可降阶的高阶方程

【基本思想】

求解可降阶的高阶方程的基本思想就是 降阶
此处以二阶可降阶微分方程为例说明，高于二阶的可降解方程亦是如此

  二阶可降阶微分方程的一般形式：
$$y^{\prime \prime }=f(x,y,y^{\prime })$$

7.3.1 $y^{(n)}=f(x)$ 型

多次求积分即可

7.3.2 不显含y型

$$y^{\prime \prime }=f(x,y^{\prime })$$
【求解方法】

7.3.3 不显含x型

【真】

【Notes】
  上述高阶可降阶的方程均以二阶为例，但同时适用于更高阶。换言之，降阶是处理高阶方程的一般思想，其不局限于二阶。

7.4 高阶线性微分方程

先研究解的结构，再研究解的方法，
若有解，是唯一还是无穷多
若是无穷多，则最关键的是哪几个（引入基础解系）

7.4.1 线性微分方程的解的结构

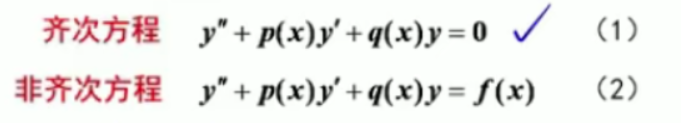
【定理 1】

  如果 $y_1(x)$ 和 $y_2(x)$ 是齐次方程的两个线性无关的特解，则：
$$y=C_1{y}_1(x)+C_2{y}_2(x)$$
就是该齐次方程的通解

对于给定的一个方程，如何找出其线性无关的特解？目前还没有一般方法，所以这里一般停留在理论上

【定理 2】

  如果 $y_1(x)$ 和 $y_2(x)$ 是齐次方程的两个线性无关的特解，且 $y^{\ast }$ 是对应非齐次方程的一个特解，则此非齐次方程的通解为：
$$y=C_1{y}_1(x)+C_2{y}_2(x)+y^{\ast }(x)$$

【定理 3】

  如果 $y_1^{\ast }(x)$ 和 $y_2^{\ast }(x)$ 是非齐次方程的两个特解，则：
$$y(x)=y_1^{\ast }(x)-y_2^{\ast }(x)$$
是对应齐次方程的解

非齐次方程的解关于非齐次项具有叠加性

上述四个定理，重点是前两个，前两个解决了关于齐次和非齐次通解的问题

再次强调，对于一个齐次方程，找两个线性无关的解，仍停留在理论阶段，目前还没有一般的方法。
而对于其特殊情况，则有解决方法（特殊情况指的是常系数，而一般情况指的是变系数）

【定理】
  如果 $y_1(x)$

7.4.2 常系数齐次线性微分方程

对于变系数齐次线性微分方程，没有找两个线性无关的特解的方法，而对于常系数齐次线性微分方程，则有

【求解方法】

先找特征方程
求特征方程的根，通过两个根的情况，从而确定解的形式

这种方法将微分方程求解的问题转换成代数方程求根的问题

这里是以二阶为例进行说明，但若是三阶四阶，这种方法仍然适用

历年考研大多为二阶，但也考过三阶

【真】

对于根不同的形式有着不同的通解形式，同时，需要凭借不同的通解形式来判断原方程对应特征方程的根的情况

7.4.3 常系数非齐次线性微分方程

对于常系数非齐次线性微分方程，目前只需掌握 $f(x)$ 两种形式的求解方式

1、$f(x)$ 为

指数乘多项式的形式，使用的是待定系数法

【真】

设定的特解中的 $x^k$ 中的 $k$ ，指的是特征方程含根 $\lambda$ 的重复次数

2、$f(x)$ 为

指数乘多项式再乘三角函数的形式，同样使用的是待定系数法

【真】

7.4.4 欧拉方程

仅数一，且指考过一次
欧拉方程有着特殊的线性变系数，即n阶导前含有x的n次方。
对于线性变系数，没有一
般的求解方法，而对于线性常系数，目前可以解决，故可尝试将线性变系数转化为线性常系数

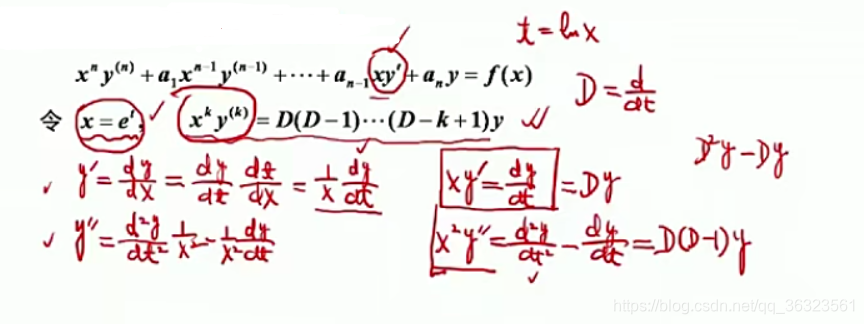
【解法】

令 $x=e^t$ ，目的是将原来的线性变系数化成常系数

【真】