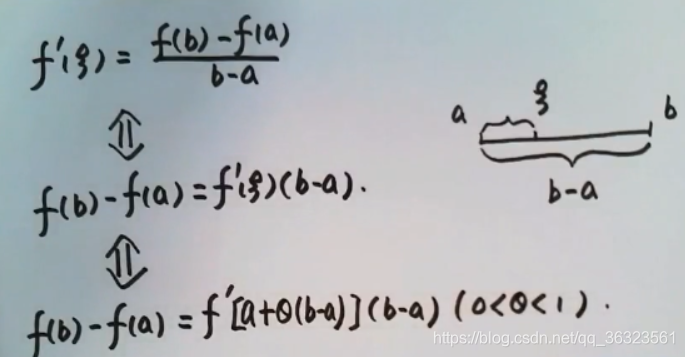第三章——微分中值定理及导数应用

---

---

一、微分中值定理

费马定理
罗尔定理
拉格朗日中值定理
柯西中值定理
泰勒公式
中值定理的几个推广*
积分中值定理*

（一）费马引理

（二）罗尔定理

罗尔定理有三个条件：
1、闭区间连续；
2、开区间可导；
3、两点函数值相等（这是最致命的条件）。

若 1）$f(x)$ 在 $[a,b]$ 上连续；
  2）$f(x)$ 在 $(a,b)$ 内可导；
  3）$f(a)=f(b)$；
则 $存在\xi 属于(a,b)$，使 $f^{\prime }(\xi )=0$.

【Notes】：

1、$\xi$ 一定是开区间，即 $\xi 属于(a,b)$；
2、$\xi$ 至少存在一个

【罗尔定理的证明】

对于罗尔定理，设函数在定义域内有最大值M和最小值m
1、m=M时，即函数为常函数，任一点的导数值横为0
2、m<M时，

【题型：证明$f^n(\xi )=0$】：

• 证明一个函数在一个点处若干阶导数为0
• 这种题型实际上是罗尔型的命题
• 这里的n一般不会太大，最多会是3

（三）拉格朗日中值定理

罗尔定理由于条件的限制（所需条件过多，指的就是需要两点函数值相等），所以并不算是一个好用的定理。


而拉格朗日中值定理没有 “两点函数值相等” 这一条件的限制；
所以只有两个条件：
1、闭区间连续
2、开区间可导

如果函数 $f(x)$ 满足以下条件：
（1）在闭区间上连续，
（2）在开区间内可导，
则在 $(a,b)$ 内至少存在一点 $\xi$ ，使得
$$f(b)-f(a)=f^{\prime }(\xi )(b-a)$$

扫描二维码关注公众号，回复： 13110385 查看本文章

【Notes】

1、中值至少存在一个
2、若增加条件（两点函数值相等），此时拉格朗日中值定理变为罗尔中值定理

	罗尔定理	拉格朗日中值定理
条件	①闭区间连续 ②开区间可导 ③两点函数值相等	①闭区间连续 ②开区间可导

3、拉格朗日中值定理的其他形式
$f(b)-f(a)=f^{\prime }(\xi )(b-a)=f^{\prime }[a+\theta (b-a)](b-a),0<\theta <1$

4、拉格朗日中值定理的用法

• ① 见到函数值之差，用拉格朗日中值定理
• ② 题干出现三个函数值，通常用两次拉格朗日中值定理
• ③ 题干中出现“$f\to f^{\prime }$”，此时有可能用拉个朗日中值定理，也有可能是积分中值定理

5、拉格朗日中值定理的证明

（四）柯西中值定理

三个条件

• 闭区间连续
• 开区间可导
• （位于分母处的函数的导函数不为零）
  

【Notes】

① 第三个条件的作用

" $g^{\prime }(x)\ne 0$ " ，说明柯西中值定理无论是左边还是右边，分母都不可能为零；
② 若 $g(x)=x$ ，则柯西变成拉格朗日；
③ 柯西中值定理的证明

④ 柯西中值定理后出现双中值型题型，详见中值定理证明专题

【罗尔定理、拉格朗日中值定理、柯西中值定理三个定理的本质】：
建立了$f^{\prime }(x)$与$f(x)$之间的联系，为后面用导数研究函数奠定了基础

其中，罗尔定理也是建立了导数与函数之间的关系，可将0视为$f(b)-f(a)$。

使用微分中值定理的情况：
题干中告诉导数的条件，让其研究函数

【罗尔定理、拉格朗日中值定理、柯西中值定理之间的关系】：

• 对于柯西中值定理，取$F(x)=x$，则得到拉格朗日中值定理，即拉格朗日中值定理是柯西中值定理的特例。
• 对于拉格朗日中值定理，取条件$f(b)=f(a)$，则得到罗尔定理，即罗尔定理是拉格朗日中值定理的特例。

罗尔	拉格朗日	柯西
（最特例）		（最一般）

从右往左叫特例的关系；
从左往右加推广的关系

即用罗尔或拉格朗日能证出的题目，柯西一定可以证出
（但是学习重点是罗尔和拉格朗日，因为这两个使用频率高，且相对用着方便）
（虽然拉格朗日和柯西都是罗尔的推广，但是这两个的证明都是用罗尔定理构造辅助函数所证得，所以罗尔定理的地位更高，即凡是用拉格朗日或柯西解决的问题，用柯西一定可以解决）

（后面微分中值定理的证明，很多都要用到罗尔）

前三个微分中值定理建立了导数与函数之间的关系，但仅仅只是建立了一阶导数与函数之间的关系，当涉及到高阶导数是，我们需要引入泰勒公式来建立高阶导数与函数之间的关系

（五）泰勒公式

定理5（皮亚诺型余项泰勒公式）

定理6（拉格朗日型余项泰勒公式）

【（两个）泰勒公式的本质】：
是建立$f(x)$与$f^n(x)$之间的关系，为我们用高阶导数研究函数奠定了基础。

（即函数与高阶导数之间的关系）

【（两个）泰勒公式的另一个注意点】：
泰勒公式能把任一个函数写成一个多项式加上一个余项（只是余项的形式不一样）是用多项式来逼近这个函数。之所以用多项式逼近这个一般的函数，是因为多项式函数在微积分中的三大基本运算都简单（多项式求极限、多项式求导数、多项式求积分）

【两个泰勒公式的不同点】：

不同点	皮亚诺型	拉格朗日型
条件不同	在点 $x_0$ 处 $n$ 阶可导	在含有 $x_0$ 的开区间 $(a,b)$ 内有 $n+1$ 阶导数
余项不同	皮亚诺余项	拉格朗日余项

• （皮亚诺余项是一个定性的描述，这个余项代表用多项式逼近 $f(x)$ 时的误差，所以能保证误差比较小，所以把皮亚诺余项型泰勒公式称为局部泰勒公式）

• （拉格朗日余项的泰勒公式给了余项的具体表达式，可以证明，当 $n$ 无限增大时，这个余项在一个这个区间上是趋向 $0$ 的，所以也把拉格朗日余项的泰勒公式称为整体泰勒公式）

【两种泰勒公式该怎么选用？】：
两种泰勒公式都是研究函数与高阶导数之间的联系，
而局部泰勒公式研究的是局部性态；
整体泰勒公式研究的是整体性态。

【什么叫局部性态？】：
比如说函数在某一点的极限、极值

【什么叫整体性态？】：
比如与极值对应的最值（最值强调的是一个区间上，它是一个整体性态而不是一个局部性态）又比如证明不等式（注意不是说邻域，这里强调的是区间）

【$x_0$ 该怎么选？】：
题目里哪一点提供关于这个函数的导数的信息多，$x_0$ 就选谁。

【几个具体的泰勒公式】：

如上图所示，箭头所指也是一个中值，所以将泰勒公式同上面三个中值定理合称四大中值定理（罗尔定理，拉格朗日中值定理、柯西中值定理、带有拉格朗日余项的泰勒公式）

（六）中值定理的几个推广形式

 推论1（导数零点定理）

 推论2（导数介值定理）

 推论3（泰勒中值定理的推广）

这是什么？

（七）积分中值定理 *

这不属于微分中值定理的部分，后面将在《第四章——定积分》进行讲解

二、导数应用

在习得上述中值定理后，可以通过导数与函数之间的关系，以导数作为工具来研究函数的一系列性态

（一）单调性问题

【（用导数研究）函数的单调性】
函数的单调问题归结为导数的正负问题

（二）极值问题

1、极值点

极值点是指 $x$ 轴上的点，如： $x=x_0$
极大点 = 极大值点
极小点 = 极小值点

2、极值

【 （用导数研究）函数的极值】

极大值与极小值统称为极值，而使其取极值的点 $x=x_0$ 被称为极值点

【充分条件与必要条件】

极值点这里有
一个必要条件
两个充分条件

【定理8 （极值的必要条件）】：

导数等于零 是 可导函数在某点取得极值 的必要条件

（解释）
函数在某一点处取到极值，那么这一点的导数一定是等于0
但反过来，导数为0的点，不一定是极值点

这里引入一个概念——驻点
【驻点】

导数为 $0$ 的 $x$ 轴上的点被称为函数的驻点

这里有两点需要注意：
① 该点处需要导数存在
② 导数值为零

【易错易混】：

• 极值点就是驻点
  极值点不是驻点，极值点不一定是可导点，不一定满足驻点定义
• 【极值点与驻点之间的关系】：
  • 若 $f(x)$ 非可导，则
    - 极值点不一定是驻点；
    （如 $f(x)=|x|$ ，显然在 $x=0$ 有极值，但是在 $x=0$ 处不可导，所以没有驻点）
    - 驻点不一定是极值点。
    （虽然驻点上的导数为 $0$，但导数为 $0$ 的点不一定是极值点）
  • 若 $f(x)$ 可导，则
    - 此时极值点一定是驻点；
    - 而驻点不一定是极值点。

【一个函数可能取得极值的点（这里指 $x_0$）有且可能只有两种】：
第一种是 导数等于0：$f^{\prime }(x_0)=0$ 的点
第二种是 导数不存在：$f^{\prime }(x_0)$ 不存在的点

具体是不是极值点，则需要用充分条件进行判定

【定理9（极值的第一充分条件）】

以下两种情况才可使用第一充分：$f(x)$ 在 $x=x_0$ 处可导，或者导数不存在这两种

• 当在 $x_0$ 处可导，则保证了 $f(x)$ 在 $x_0$ 邻域内可导；
• 当在 $x_0$ 处不可导，但需要保证在 $x=x_0$ 处连续，也满足第一充分条件的使用条件

概括为：
在满足条件的基础上，在 $x=x_0$ 两侧，一阶导数变号，则这一点肯定有极值
即，看驻点两侧一阶导数是否变号

需要注意，极值可能出现的地方只有两种点，一种是驻点，另一种就是导数不存在的点

【解释】
首先需要在去心邻域可导，其次
1、若 $x=x_0$ 处导数为零，说明是驻点，则 $x=x_0$ 为极值点
2、若 $x=x_0$ 处导数不存在（但在这一点连续），也能说明 $x=x_0$ 为极值点

【优劣】

优势	劣势
既可以判定驻点上有没有取得极值；也可以判定导数不存在的点上有没有取得极值	待定点两侧一阶导是否变号可能不便求得（此时引入第二充分条件）

【定理10 （极值的第二充分条件）】

使用二阶导，
一阶导为零，二阶导不为零，则该点一定有极值

【优劣】

优势	劣势
不用判断 $x=x_0$ 一阶导左右是否变号	对函数的要求提高，要求一、二阶导数都要存在；所以只能用于判定驻点，对于一阶导不存在的点不可用

【求极值步骤】：
$S_1$：先找出所有可能取得极值的点（导数为零的点（驻点）或者导数不存在的点）
$S_2$：用充分条件做判定，便可确定极值。

（三）最大最小值问题

函数的最值问题

最值问题常见有两个问题（理论问题、应用问题）

 1、求连续函数在闭区间上的最值

最大最小值的理论问题

一个函数在端点处不能取极大值，因为极值是邻域，而端点只是一个半邻域。
所以说，在两个端点处只可能取到最值，不能取到极值
所以，在区间内部找到最大（小）值，那么也一定是极大（小）值
先把内部所有可能取的极值点都找到，再与端点值比较，便可以得出最值。

【求最值的步骤】：
$S_1$：求函数在开区间内可能的极值点（即驻点和不可导点）
$S_2$：求可疑点以及端点处的函数值（最值一定在这些值里面）
$S_3$：比较以上各点

下列情况不需要和端点作比较：

若连续函数在开区间内仅有唯一极值点，其中
 若是极小值，就是最小值；
 若是极大值，就是最大值

 2、最大最小值的应用题

最大最小值的应用问题

$S_1$：建立目标函数（很关键）
题干中最大（小）量用一个变量的函数表示出来
函数的确定需要以有利于后面求最值这一过程为标准，宁愿确立函数麻烦，也不能让后面求最值的过程麻烦
$S_n$：后面的步骤同“【求最值的步骤】”

（四）曲线的凹凸性

定义 3 凹凸性

曲线凹凸性的定义由图像刻画最明显，但是不方便。

所以用二阶导数的正负用来判定曲线的凹凸性
定理11

一阶导数的正负刻画函数的增减性
二阶导数的正负刻画函数的凹凸性

  拐点

曲线凹凸性发生变化的点（面上的 点）
（极值点是x轴上的点（线上的点））

【拐点的判定（必要条件与充分条件）】
这里同样也是一个必要两个充分
（对应极值点的一个必要两个充分）
可同极值点一起理解记忆
区别在于这里将导数阶数统统抬高一阶

【定理（拐点的必要条件）】

且点 $(x_0,f(x_0))$ 为曲线 $y=f(x)$ 的拐点

【定理（拐点的第一充分条件）】

设 $y=f(x)$ 在点 $x_0$ 的某去心邻域内二阶可导，且 $f^{\prime \prime }(x_0)=0$ （或 $f(x)$ 在 $x_0$ 处连续）.
  (1)

	极值点	拐点
必要条件	一阶导为 $0$	二阶导为 $0$
第一充分条件	一阶导为0，一阶导两侧变号	二阶导为0，二阶导两侧变号
第二充分条件	一阶导为0，二阶导不为0	二阶导为0，三阶导不为0

（五）渐近线

渐近线有三种：水平渐近线、垂直渐近线、斜渐近线

1、水平渐近线

一条曲线最多可以有两条水平渐近线，
两个方向可以有不同的水平渐近线
（如：$arctanx$）

2、垂直渐近线

一条曲线最多可以有无数条垂直渐近线
如：$tanx$

• 因为垂直渐近线极限趋向无穷，所以分母为0的点一般是可疑点

若
  ${\lim }_{x\to x_0}f(x)=\infty$（或 ${\lim }_{x\to x_0^{-}}f(x)=\infty$，或 ${\lim }_{x\to x_0^{+}}f(x)=\infty$）
那么
  $x=x_0$ 是曲线 $y=f(x)$ 的垂直渐近线


【求垂直渐近线】

$S_1$：先找间断点
  一般是函数的无定义点


$S_2$：间断点处取极限
  左右极限任意一侧趋于 $\infty$ 即存在垂直渐近线

【Notes】

• 对于垂直渐近线
  间断点处任意一侧极限趋于 $\infty$ 即可证明垂直渐近线存在

3、斜渐近线

在一条曲线的某一侧，水平渐近线与斜渐近线最多只能存在其中一个。

（六）函数作图

【作图步骤】：
S_1、找定义域
S_2、求一阶导数

目的是为了找单调区间，进而确定极值

S_3、求二阶导数

目的是为了确定凹凸区间，以及拐点

S_4、求渐近线

实质上函数作图是对上述内容的综合应用

（七）曲线的弧微分与曲率

 1、曲线的弧微分

【弧微分基本公式】

$(ds{)}^2=(dx{)}^2+(dy{)}^2$

（1）直角坐标系下的弧微分

设 $L$：$y=f(x)$，则 $ds=\sqrt{1+f^{\prime 2}(x)}dx$；

（2）参数方程形式的弧微分

设 $L$：$\{\begin{array}{l}x=\varphi (t),\\ y=\psi (t),\end{array}$则 $ds=\sqrt{{\varphi }^{\prime 2}(t)+{\psi }^{\prime 2}(t)}dt$；

（3）极坐标形式的弧微分

设 $L$：$r=r(\theta )$，则 $ds=\sqrt{r^2(\theta )+r^{\prime 2}(\theta )}d\theta$.

 2、曲线的曲率

描述曲线的弯曲程度

（1）曲率
$$K=\frac{|y^{\prime \prime }|}{(1+y^{\prime 2}{)}^{\frac{3}{2}}}$$

（2）曲率半径
$$R=\frac{1}{K}$$

三、常考题型与典型例题

（一）求函数的极值和最值及确定曲线的凹向和拐点向

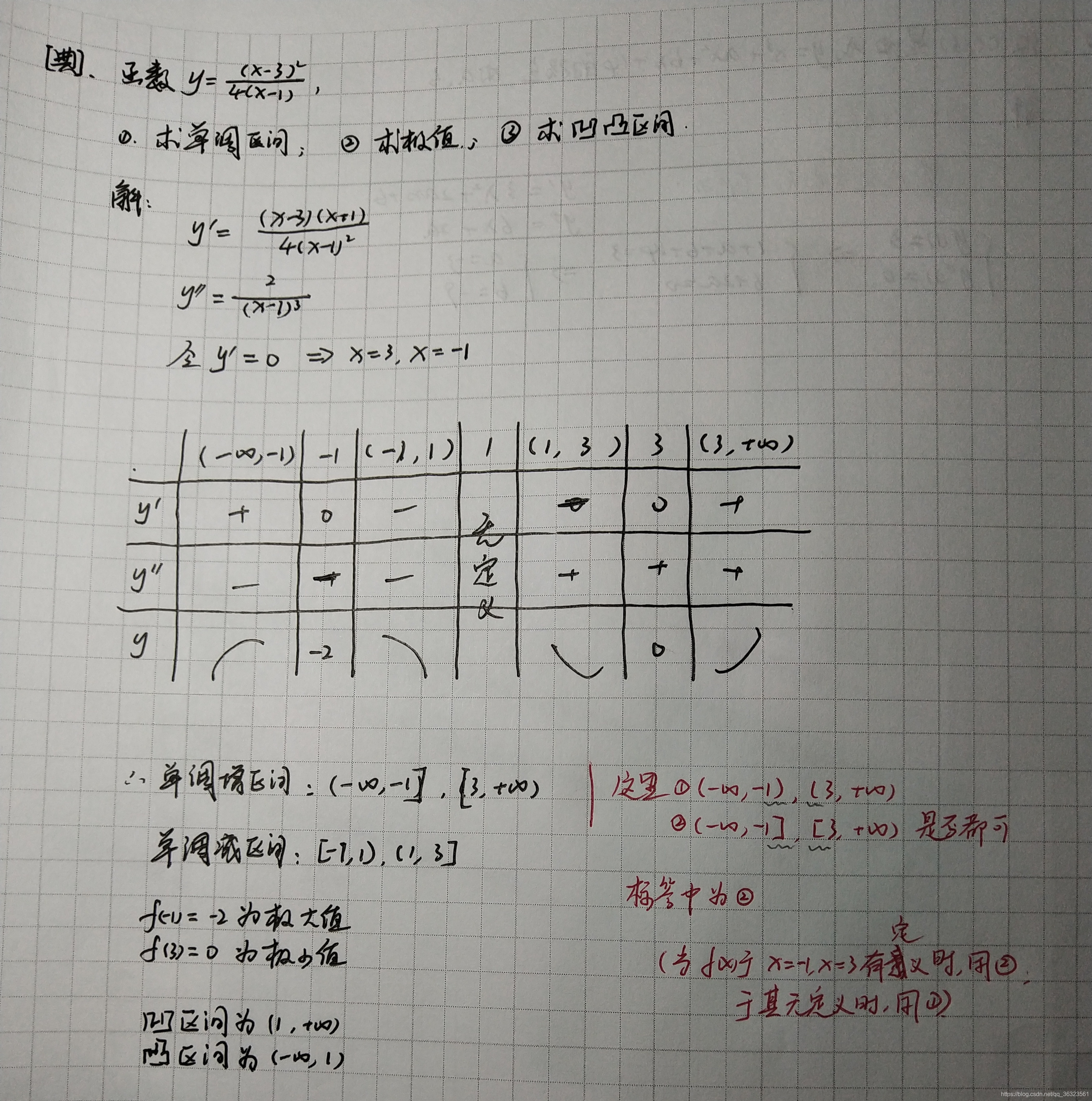
【例】

• 极值点只有两种“存在形式”
  • 驻点
  • 导数不存在的点
• 注意题干说明，图像为一阶导数图像，而不是函数图像
  

【例】

【例】

【例】

【例】

【典】拐点

拐点所对应的点处的二阶导数为零

【典】求单调区间、凹凸区间

（二）求渐近线

历年常考题型，常出现在选填中。

【例】

【例】

【例】

【题】求渐近线

求渐近线的常规题

（三）方程的根

求方程的根等价于求对应函数的零点
这里主要有两个问题：

• 1、方程根的存在性（实质为 $f(x)$ 零点的存在性）
• 2、方程根的个数

 1、方程根的存在性

常用方法：连续函数的零点定理 | 罗尔定理

连续函数的零点定理有两个条件：
 一是函数在闭区间连续；
 二是函数两端点处函数值异号。

当使用零点定理的条件不满足时（一般是第二个条件不好验证），此时用罗尔定理
即找到 $f(x)$ 的一个原函数 $F(x)$，此时 $f(x)=0$ 即 $F^{\prime }(x)=0$。

 2、方程根的个数问题

常用方法：单调性 | 罗尔定理推论

一般由存在性得存在，再由单调性证明唯一

罗尔定理推论：
 如果一个函数 $n$ 阶导数不为零，问方程 $f(x)=0$ 最多多少根（强化班讲）

【例】

在这里插入图片描述

【例】

（四）不等式的证明

常用方法：单调性 | 拉格朗日中值定理 | 最大最小值的方法

待证不等式往往需要观察整理

• 方法一：（使用频率最高）
  使用场景：导数简单，正负易于判断
  如：求证$f(x)>=g(x)x属于[a,b]$
  方法：令 $F(x)=f(x)-g(x)>=0$
  只需证出：$F(a)=0,F^{\prime }(x)>0$ 即可
• 方法二：
  出现同一函数在两点处函数值的差，此时用拉格朗日中值定理

两个常用基本不等式：

【例】

【例】

【例】

（五）中值定理的证明

目前只是一些基础题

【例】

• 很多真题都是基于本题改编的
• $n$ 个点函数值相同，则可通过多次罗尔定理得出最多存在 $(n-1)$ 阶导为零
  

---

【例】

本题在证明导数大于零时，在右端点大于左端点处用拉格朗日
在证明导数小于零时，在右端点小于左端点处用拉格朗日

【例】

由上题一阶导数不同区间使用拉格朗日的思想，延伸到对二阶导数使用拉格朗日
在一阶导数不同区间使用拉格朗日，从而创造对二阶导数使用拉格朗日的条件

【例】

• 第（1）问可用介值定理，也可用零点定理
• 构造辅助函数是一个常规方法
  

四、中值定理证明题专题（汤家凤）

（一）证明 $n$ 阶导为零

证明一个函数在某点处的若干阶导为零，可认其为罗尔型命题

【例】

【例】

（二）待证结论仅含有一个中值

当待证结论中只有一个中值时，一般根据结论的具体形式，分为以下三种解答方式：


方法一：还原法
  当待证结论满足以下三个特征，则用还原法，具体特征如下：

• 待证结论只有一个中值，如：$\xi$
• 待证结论只有两项
• 待证结论两项中的导数阶数相差一阶
  
  

方法二：分组构造法
  当不满足还原法的三个特征时，一般用分组构造法。

• 一是待证结论多于两项，则用分组构造法使其满足还原法条件，再用还原法解答；
• 二是待证结论导数阶数相差不止一阶，则通过加一项减一项来补充，在用分组构造使其满足还原法的条件，最后用还原法解答。

方法三：未见到，后续补充

[情形一：还原法]

【例】还原法题型

还原法：
注意三个特征

• 只有一个中值
• 两项
• 差一阶
  

[情形二：分组构造法]

【例】分组法解题

本题不满足还原法的三特征，使用的是分组构造法；进而满足还原法特征，再使用的还原法。

（三）拉个朗日中值定理的用法

【例】见同函数相减，用拉

同一函数不同函数值相减，一般直接用拉格朗日

【例】见同函数相减用拉

同一函数不同函数值相减，一般直接用拉格朗日

【联想】

• 见到函数值相加，拿到手就要想到介值定理
• 介值定理为闭区间，零点定理为开区间

【例】见三点函数值，通常两次拉格朗日

【例】

（四）待证结论中有至少两个中值

  情形一：只有 $f^{\prime }(\xi )$ 和 $f^{\prime }(\eta )$ 的形式

除此之外只可有常数，不可有其他的有关中值的任意形式存在

【例】双中值_情形一

【例】

  情形二：$\xi$、$\eta$ 复杂度不同

曾经是主流题型
视 $\xi$，$\eta$ 为两部分，保留复杂部分

其中，复杂部分有两种

① 复杂部分为一阶导形式，则用拉格朗日

② 复杂部分为一阶导之比的形式，则用柯西

【例】双中值的情形二（两个中值复杂度不同）

【例】

（五）待证结论中含有 $a$、$b$、$\xi$

这里注意，只有一个中值，以及两个待定字母
（前面所见的为两个中值，两个待定字母，勿混淆）

  这类问题通常有两种情形：
第一：待定字母与单中值可分离

将待定字母与中值分离，处理待定字母部分
由表达式性质进而决定用拉格朗日或是柯西（一般就这两种，别无他法）

第二：待定字母与单中值不可分离

（以后补充）

情形一：可分离型

【例】

【例】

情形二：不可分离型

五、错题

【错】

【错】