Graph WaveNet for Deep Spatial-Temporal Graph Modeling
研究问题
解决时序预测时如何自动学习出一个图结构的问题，之前组会讲过一篇KDD2020发表的《Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks》也是针对自动学习图结构，感觉借鉴了很多这篇19年论文的思想，在下面也对两篇论文做一些对比。
背景动机
- 传统提取空间信息的方法一般是在固定的图结构上提取输入特征，但是固定的图结构不一定能反映真实的依赖关系，比如要么图中存在的连接在现实中不存在，要么是现实存在的连接在图中不存在，对于前者可以对图上的连接权重引入attention来实现，对于后面这种情况目前却没有很好的解决办法
- 传统提取时间信息的方法一般基于RNN或CNN，对于RNN，其主要缺点在于迭代计算的过程较为耗时，且容易遇到梯度爆炸或梯度消失，对于CNN，其主要缺点在于难以取得足够大的感受野
模型思想
构造一个自适应邻接矩阵来学习图结构，使用引入空洞卷积的因果卷积来扩大CNN的感受野
符号定义
- 图相关
图的定义
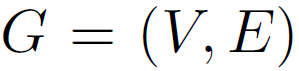
邻接矩阵:
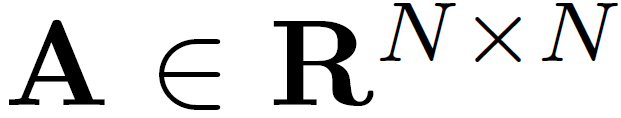
t时刻的特征矩阵/图信号：
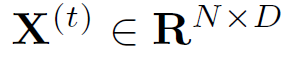
- 预测相关
根据前S个时间步预测后T个时间步：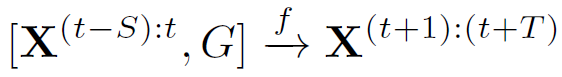
模型结构
- 自适应邻接矩阵的计算
作者提出要随机初始化两个可学习的节点嵌入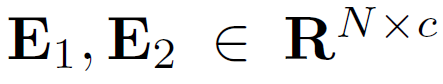
，然后可学习的邻接矩阵的计算公式就可以定义如下，其中softmax是为了进行归一化处理：
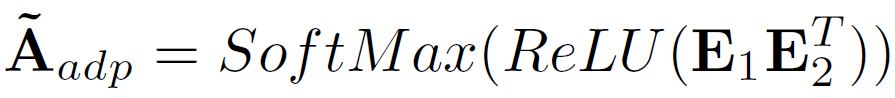
对比一下另外一篇文章的计算方式是下面这样的，其实就是加入了邻接矩阵要满足非对称性的额外要求
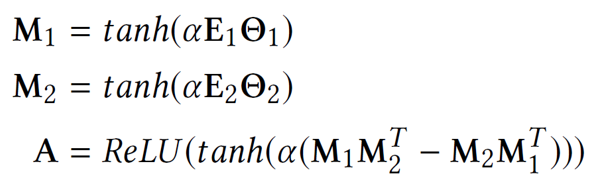
但是本文的公式明显更简单一点，且文中说E1代表源节点嵌入，E2代表目标节点嵌入，二者相乘代表从源节点到目标节点的空间依赖关系，明显解释性更强一些。
- 图卷积计算公式（diffusion convolution）
对于图结构完全未知的情况，只有自学习邻接矩阵可以用来计算，因此计算公式为
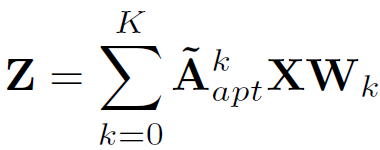
对于已有图结构的情况，可以将二者结合，并对已有图结构的邻接矩阵分别按前向后向两个方向计算
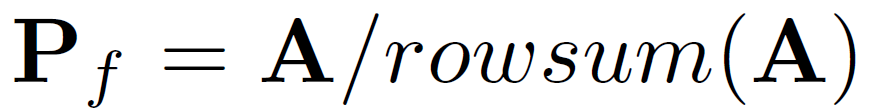
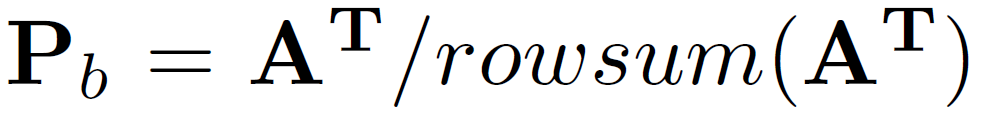
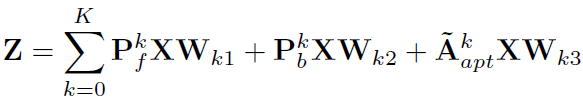
另一篇论文主要的改动是在对每一层卷积的结果按attention求和计算Z，并与未经过卷积的结果进行加权
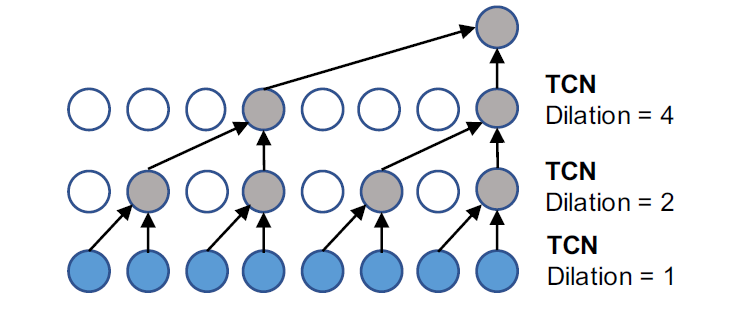
- 空洞因果卷积
其示意图如下，主要的优势在于感受野随层数指数增长，因此在层数不变的情况下可以获得更大的时间尺度的信息
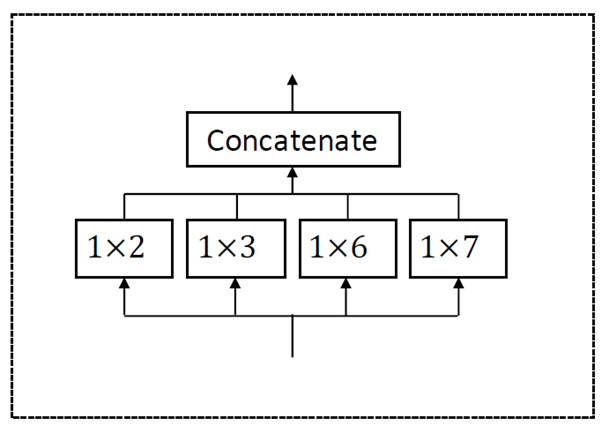
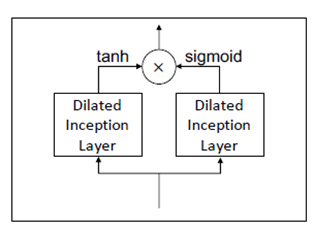
同样，另一篇论文也借鉴了空洞卷积的思想，不过它采用的不是因果卷积而是同一层的多个卷积（inception layer）。
- 门控时间卷积
令 Θ 1 , Θ 2 \Theta_{1}, \Theta_{2} Θ1,Θ2，b，c为模型参数，门控卷积的计算过程如下，g为激活函数，σ为sigmod函数
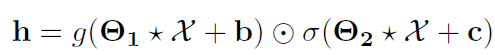
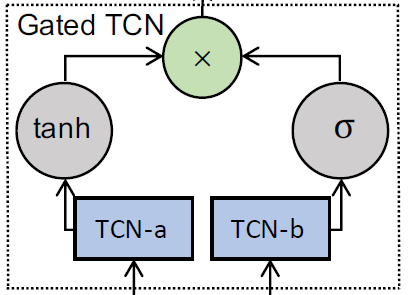
另一篇论文完全复制了这个设定，连图都一模一样
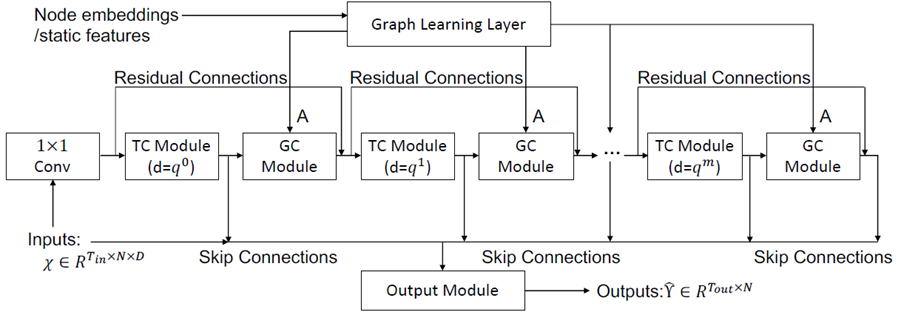
- 总体框架
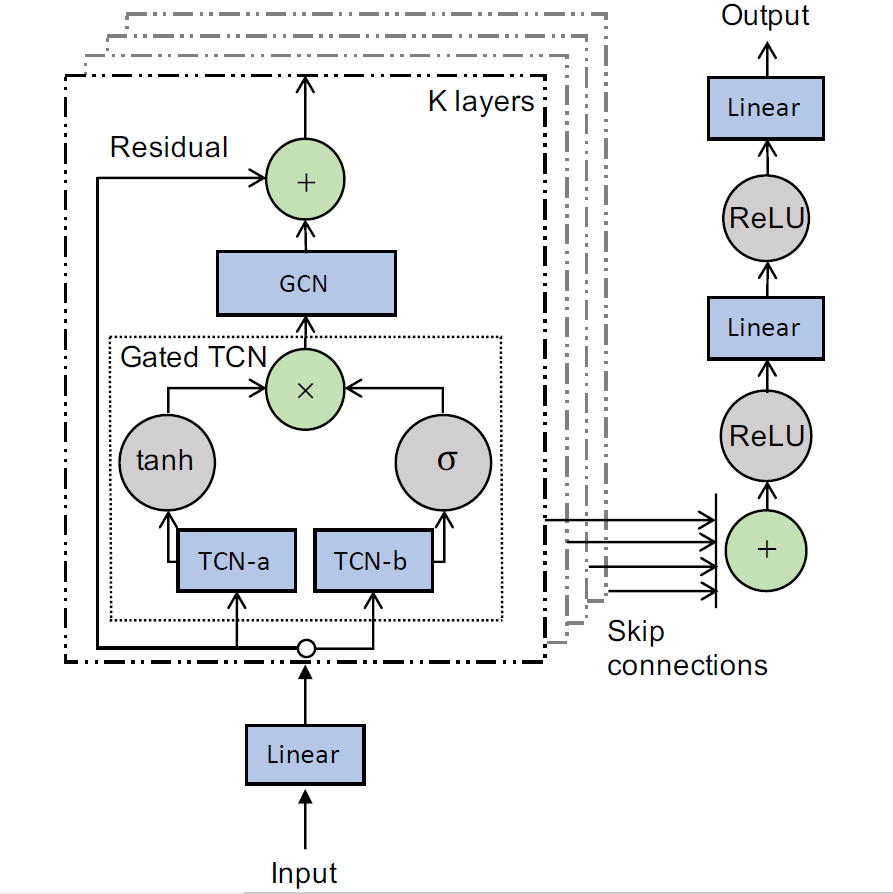
左侧是模型的输入部分，原始数据经过线性变换之后与K个时空层相连以提取时间空间依赖，每个时空层都包含一个门控时间卷积和图卷积，层与层之间用有残差连接，通过skip-connection得到最终结果。
另一篇论文也采用了几乎一模一样的结构，只不过把最后用线性层输出结果改成了用卷积来输出结果。
