统计学习-基本统计分布简介
初探基本统计分布
在接触统计分布的时候,我们发现概率是一种事件发生的可能性,如果一件事情的所有可能性都能罗列出来的时候,并且在数据量很大的时候或是反复实验的时候,这些概率符合一个函数或是一种规律,那么我们就建立起事件发生的描述和事件发生的可能性的一个映射关系,这种关系其实就是统计分布函数。下面我们来介绍一些基本的分布函数,而其中的细节和思路我们会用抛硬币来进行说明。
首先介绍的是伯努利分布,这种分布可以理解一次事件发生的可能性,并且可能性只有2种,这个时候用抛硬币理解伯努利分布就是抛一次硬币,发生正面的可能性可以用下面的概率分布来衡量,也就是所谓的P(x|p) ,下面是概率表达和期望以及方差的表达式,可以很直观的理解。显然正常的硬币抛到正面的概率是1/2,而此时P(1|x)的概率显然是1/2 ,而发生的期望和方差也是如下面的公式计算一样,分别是1/2和1/4,但如果硬币的正面比较不规则或是存在轻重不均匀的情况,这个概率可能发生变化,也就是p可能是0.7或者是0.3,这个时候伯努利公式还是能准确描述的。
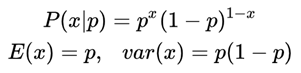
其次是介绍二项分布,这种分布是重复N次伯努利试验得到的,它的表达式当次数是1的时候,就是伯努利分布的表达式,其中这种分布描述的也是一种事件如果发生的可能性只有两种情况的时候,多次实验或是经常发生的时候,可以用二项分布表达它发生的概率。这个时候需要注意的是,二项分布有一个假设,也就是每一次实验都是独立发生的,和之前或是之后发生的事件都是无关的,那么我们用抛硬币理解就是,抛硬币n次,其中每次抛到正面的概率是p,那么在n次抛掷的时候,得到k次正面的概率可以描述为,而期望和方差是在原有的伯努利分布的基础上乘以n次,显然二项分布就是伯努利的分布的扩展,其中C(n,k) 就是一个n次抛掷里出现k次正面的组合计算结果。
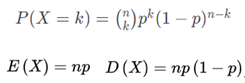
然后我们继续介绍泊松分布,这种分布是二项分布的近似,使用的情况是当发生次数n非常大,概率p非常小的时候,可以使用泊松分布进行近似逼近或者计算,这个n至少取20,而p应该小于0.05,因为从二项分布的公式我们就可以发现,它要计算概率的幂级数的连乘计算,非常耗时,所以当某些特殊情况可以使用泊松分布进行逼近。那么它的近似步骤如下,使用λ去表达期望np,然后当n取到比较大的值的时候,可以近似得到最终的表达式,这样有一个好处,我们只需要期望和某一种情况发生的次数就可以近似去计算概率分布。当然需要注意的是,泊松分布只能在某些场景进行使用,不是适用所有的情况。
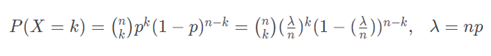
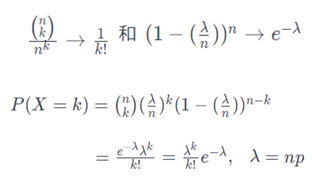
总的来说,了解数据的分布对数据理解有帮助,因为分析者可以从分布感受到数据的形态,或是观察出数据的某些特征,或是从宏观的角度去观察数据。对于不同的分布,使用的场景是不一样的,使用者需要先对事物进行建模后,才能决定使用哪一种分布来解决问题,所以统计从业者必须要深刻理解分布,在工作和学习中会经常使用到。