图论-图论算法之Louvain
社区发现算法简介之Louvain算法
在本次文章中,我们将会介绍经典的社区发现方法,也就是Louvain算法。这种算法在社群发现等应用的效果较好,是比较经典的图挖掘类算法,在金融风控行业挖掘诈骗团伙等应用里有比较显著的效果。社区发现方法的目标是在整个图里面发现一些有聚集性特征的群体,这些群体的特征是内部的互相联系较为紧密,外部和其他点的联系较为稀疏。下面我们对算法思路和步骤进行介绍。
Louvain算法的核心就是模块度的计算,它每一次将模块度变化更大的邻居团伙作为当前点的目标团伙,反复计算迭代后可以得到最终的社团发现结果。其中模块度的计算公式如下所示,我们发现其中A其实就是全图的邻接矩阵的某个位置的元素,而m其实是A矩阵所有元素的求和结果,这个公式的最后面有一个0-1函数,它的作用是如果两个点不属于同一个社区,那么将设置Q值为0,也就是不需要计算。

在得到了模块度的公式后,我们进一步求模块度的变化结果,也就是计算当新的点加入到社区的时候,对于原有两个社区的变化,而公式也是用新的模块度Q值去减去原有两个旧的模块度Q值,经过化简后得到下述的式子。其中K(i,in) 指的是当前社区内部的所有节点和新的节点i所连接的边的权值之和;而K(i) 则是所有和节点i直接相连的边的权值之和;Σtot 的含义是当前社区边内部的权重之和再加上当前社区和其他社区相连接的边的权值之和的结果。
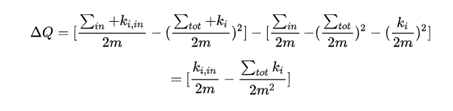
根据上述的公式,我们只需要不断的计算模块度变化值就可以了,直到迭代计算的次数达到了最大上限的次数,或者整体的模块度已经不发生变化的时候就可以结束算法。那么根据上述公式和思路,我们总结的Louvain算法步骤如下:
1)初始化参数设置,比如最大迭代次数,每个点的模块度初始值等参数。
2)遍历每个节点,比较每个节点和周围相邻社区(最开始周围社区是节点,后续的迭代中可能变成多个点聚集的社区),计算当前节点和周围社区的模块度变化,也就是ΔQ,将每个节点加入到模块度大于0并且具有最大模块度增量的社区之中,如果周围的社区计算得到的模块度增量都是小于0的,则无需操作,保留当前节点并且不加入到任意社区中。
3)对上一步骤得到的结果进行重构,也就是将各个社区重新合并,把原有的图转化为新的超图,可以认为新的社区是一个大的“节点”,而两个大的“节点”之间的边的权重就是社区内部所有节点互相的边的距离权重之和,从而构建新的超图后,再次进行迭代计算模块度变换。
4)反复重复上述步骤后,直到整体的模块度不再变化或者达到了最大的迭代次数后,停止该算法。
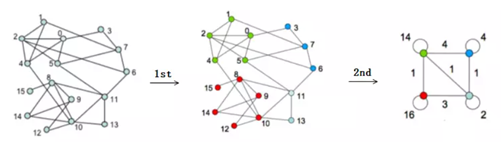
总的来说,本文提及的Louvain算法是比较经典和实用的算法,在真实场景中经常被使用,因为它本身的原理比较经典,而且算法的核心思路是符合图自身结构的聚类趋势的,但是需要注意的是Louvain算法针对的是无向图,如果是有向图则无法使用,或者尽量弱化为无向图。Louvain算法是初学者需要掌握的,可以帮助在后续学习其他算法的过程中打好基础,并且解决真实应用里的问题。