算术编码（xdu多媒体实验一）

其他 2021-04-03 16:13
0 阅读

算术编码（xdu多媒体实验一）

前言

关于本文的一些联想：
我曾读到大刘（可能是）的一本短片科幻小说集，其中有一个故事说的与算术编码有关，但当时我并不清楚其原理，非常震惊。类似居然有人提问过：如果有个飞船，在某处画个点，就能解码出一套百科全书，真的可能么？。
故事讲述的是一个外星人来到地球，然后获取了地球的所有知识，包括地球的历史，科技，自然风光等等记录。然后他们带回去的时候只是在飞船上刻了一个记号，这个记号的精度非常之高，其中承载的信息就是整个地球知识的信息熵。等到他们回去只需要测量这个记号到船头的距离就可以解码出所有的知识。
我希望看完本文你可以懂其中的道理，以及对信息论的进一步深思。虽然是个美好的科幻小说，但宇宙的时空是不连续的，精度在也不可能超过普朗克尺度，也就是说宏观的精度是有极限的，所以这篇小说只是一个美妙的幻想罢了。

本文解决的问题：

详细原理参考算数编码原理解析。实验原理并不难，但网上大部分代码未解决两个问题。本文主要旨在实现以下两方面。

  1. 不能自行计算出字符串概率。这个很好解决，但不清楚为何很多博客代码仍需手动输入各个字符概率。
  2. 不能求出左右区间内最小的二进制编码对应十进制小数。此问题需要对二进制编码了解才能算出，本文可以求出算数编码的最短二进制编码。

详细原理

请务必看完算数编码原理解析或了解原理后再读以下内容。
用例子简单介绍一下：

  1. 假设输入字符串为 A R B C R ARBCR ARBCR,那么 A ， B ， C A，B，C A，B，C出现概率为 0.2 0.2 0.2， R R R出现概率为 0.4 0.4 0.4。
  2. 在 [ 0 , 1 ] [0,1] [0,1]内 划分字符概率区间。此处按照字典序来排序即 A [ 0 , 0.2 ] A[0,0.2] A[0,0.2]， B [ 0.2 , 0.4 ] B[0.2,0.4] B[0.2,0.4]， C [ 0.4 , 0.6 ] C[0.4,0.6] C[0.4,0.6], R [ 0.6 , 1 ] R[0.6,1] R[0.6,1]。
  3. 划分概率实际上和哈夫曼编码不允许前缀码相同的意思一样，只不过算术更加精细，更接近信息熵的本质。
    假设 d e l t a delta delta为区间大小，初始左边界 l o w = 0.0 low=0.0 low=0.0，右边界 h i g h = 1.0 high=1.0 high=1.0，那么 d e l t a = 1.0 delta=1.0 delta=1.0。字符 c h a r char char的区间为 [ L , R ] [L,R] [L,R]。
  4. 我们想要对第一个 A [ 0 , 0.2 ] A[0,0.2] A[0,0.2]进行编码,更新左边界 l o w = l o w + d e l t a ∗ L low=low+delta*L low=low+delta∗L,那么 l o w = 0 + 1.0 ∗ 0 = 0 low=0+1.0*0=0 low=0+1.0∗0=0。同理右边界 h i g h = 0 + 1.0 ∗ 0.2 = 0.2 high=0+1.0*0.2=0.2 high=0+1.0∗0.2=0.2。
    再看第二个字符 R [ 0.6 , 1 ] R[0.6,1] R[0.6,1]，此时左边界更新为 l o w = 0 + 0.2 ∗ 0.6 = 0.12 low=0+0.2*0.6=0.12 low=0+0.2∗0.6=0.12，右边界 h i g h = 0 + 0.2 ∗ 1 = 0.2 high=0+0.2*1=0.2 high=0+0.2∗1=0.2。
    依次类推，最终得到区间 [ 0.14432 , 0.1456 ] [0.14432,0.1456] [0.14432,0.1456]。其中抽取任意一个值就可以利用字符概率表得到原字符串。

原理部分并不难，主要是左右边界的迭代，公式为：
l o w = l o w + ( h i g h − l o w ) ∗ L low=low+(high−low)∗L low=low+(high−low)∗L
h i g h = l o w + ( h i g h − l o w ) ∗ H high=low+(high−low)∗H high=low+(high−low)∗H

代码实现如下：

double low = 0.0;
	double high = 1.0;
	for (auto it = str.begin(); it != str.end(); it++) {
    
    
		double delta = high - low;
		high = low + delta * mp[*it].high;
		low = low + delta * mp[*it].low;
	}

然后解决我们上述所说的两个问题。
其一：怎么输入字符串后统计概率呢？
很简单，当输入字符串时，我们用一个数组记录每个数字出现的次数，由于输入的是ASCII码，我们只需建立一个大小256的数组记录次数。然后调用 s t r i n g . l e n t h ( ) string.lenth() string.lenth()函数获得长度或者提前输入字符串长度 n n n，最后用次数除以长度即可得到出现频率，频率区间按照字典序叠加即可，即字典序上一个的字母的右边界变为字典序下一个字母的左边界。最后我们将其字符及左右区间和区间长度放入map里方便查询。

const int N = 256;
int len;//长度
string str;
int char_num[N];//统计字符
struct node {
    
    //字符及概率区间
	char c;
	double l, r;
}ch[N];
struct spcode {
    
    
	double low=0.0, high=1.0, delta;//区间左右端及大小
	spcode() = default;
	spcode(double a, double b) :low(a), high(b), delta(b-a) {
    
    }
};
map<char, spcode> mp;
void create() {
    
    
	memset(char_num, 0, sizeof(char_num));
	printf("输入字符串个数n\n");
	cin >> len;
	printf("输入字符串：\n");
	cin >> str;
	for (auto i = 0; i < str.length(); i++)//统计概率
		char_num[str[i]]++;
	double last = 0.0;//字典序上一个字母频率的右边界
	for (int i = 0; i <N; i++) {
    
    
		if (char_num[i]) {
    
    //该字符出现过
			ch[i].c = i;
			ch[i].l = last;
			ch[i].r = last + double(char_num[i]) / len;
			last = ch[i].r;
		}
	}
	for (auto i = 0; i < str.length(); i++) {
    
    
		if (char_num[str[i]]) {
    
    
			mp.insert(make_pair(str[i], spcode(ch[str[i]].l,ch[str[i]].r)));
		}
	}
}

我们调用map查看其字符及左右区间和区间长度：

for (auto it = mp.begin(); it != mp.end(); it++) {
    
    
		cout << it->first <<  " (";
		cout << it->second.low << " ";
		cout << it->second.high << ") ";
		cout << it->second.delta << "\n";
	}

效果如下：
演示

扫描二维码关注公众号，回复： 13120941 查看本文章

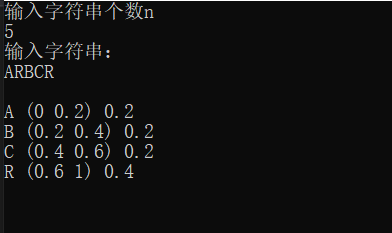
其二：在获取最终的左右区间 [ l o w , h i g h ] [low,high] [low,high]之后，怎样从中抽取出一个小数可以使其转化后的二进制编码最短？
最核心的思路显然是，当某个二进制小数在某一位后全为0，那么就可以舍弃掉，也就是确定最需要的1在哪一位。有两种思路。

  1. 十进制转二进制来考虑。既然左右边界确定了，那么对应的左右边界转为二进制，当第一次出现不一样的0，1时，说明此处最短。举个例子，左右边界转为二进制分别为0.1010011,0.101111001，第四位开始不一样，那么取0.1011即为最短的二进制表示。
  2. 二进制转十进制考虑，二进制的每一位分别对应十进制 0.5 , 0.25 , 0.125 0.5,0.25,0.125 0.5,0.25,0.125……我们初始化 a n s = 0.0 ans=0.0 ans=0.0，然后需要考虑ans加上每一位对应十进制后是否在区间内，当第一次满足在区间内时即为最短。

本文实现的是第二种方法：如果需要该位即为1，不需要为0。

	string anstr = "";
	double ans = 0.0;
	int cnt = 1;
	while (ans < low) {
    
    
		ans += pow(0.5, cnt);
		anstr += '1';
		if (ans >= high) {
    
    
			ans -= pow(0.5, cnt);
			anstr[cnt-1] = '0';
		}
		cnt++;
	}
	db = ans;
	return anstr;

源代码

演示效果如图所示：
演示
源码如下：

#include <iostream>
#include <map>
#include <string>
#include <cstring>
#include<math.h>
using namespace std;
const int N = 256;
int len;//长度
string str;
int char_num[N];//统计字符
struct node {
    
    //字符及概率区间
	char c;
	double l, r;
}ch[N];
struct spcode {
    
    
	double low=0.0, high=1.0, delta;//区间左右端及大小
	spcode() = default;
	spcode(double a, double b) :low(a), high(b), delta(b-a) {
    
    }
};
map<char, spcode> mp;
void create() {
    
    
	memset(char_num, 0, sizeof(char_num));
	printf("输入字符串个数n\n");
	cin >> len;
	printf("输入字符串：\n");
	cin >> str;
	for (auto i = 0; i < str.length(); i++)//统计概率
		char_num[str[i]]++;
	double last = 0.0;
	for (int i = 0; i <N; i++) {
    
    
		if (char_num[i]) {
    
    
			ch[i].c = i;
			ch[i].l = last;
			ch[i].r = last + double(char_num[i]) / len;
			last = ch[i].r;
		}
	}
	for (auto i = 0; i < str.length(); i++) {
    
    
		if (char_num[str[i]]) {
    
    
			mp.insert(make_pair(str[i], spcode(ch[str[i]].l,ch[str[i]].r)));
		}
	}
}
string encode(double &db,string str){
    
    
	double low = 0.0;
	double high = 1.0;
	for (auto it = str.begin(); it != str.end(); it++) {
    
    
		double delta = high - low;
		high = low + delta * mp[*it].high;
		low = low + delta * mp[*it].low;
	}
	//寻找最短二进制
	string anstr = "";
	double ans = 0.0;
	int cnt = 1;
	while (ans < low) {
    
    
		ans += pow(0.5, cnt);
		anstr += '1';
		if (ans >= high) {
    
    
			ans -= pow(0.5, cnt);
			anstr[cnt-1] = '0';
		}
		cnt++;
	}
	db = ans;
	return anstr;
}
string decode(double value) {
    
    
	double low, high;                   //编码区间
	double prelow = 0.0, prehigh = 1.0;//记录前一次
	string ans = "";
	int cur = 0;
	while (true) {
    
    
		low = prelow;
		high = prehigh;
		for (auto it = mp.begin(); it != mp.end(); it++) {
    
    
			double delta = high - low;
			high = low + delta * it->second.high;
			low = low + delta * it->second.low;
			if (value>=low && value<high) {
    
    
				prelow = low;
				prehigh = high;
				ans += (it->first);
				cur++;
				break;
			}else
			{
    
    
				low = prelow;
				high = prehigh;
			}
		}
		if (cur == len)break;
	}
	return ans;
}
int main() {
    
    
	spcode sp;
	create();
	cout << "\n";
	/*test map
	for (auto it = mp.begin(); it != mp.end(); it++) {
		cout << it->first <<  " (";
		cout << it->second.low << " ";
		cout << it->second.high << ") ";
		cout << it->second.delta << "\n";
	}
	*/
	double db;
	string anstr = encode(db, str);
	cout << "转化为小数的最短十进制表示为:\n" << db << endl;
	cout << "\n";
	cout << "最短二进制码为:\n" << anstr << endl;
	cout << "\n";
	string destr=decode(db);
	cout <<"解码后的字符串为: \n"<< destr << endl;

	return 0;
}

猜你喜欢

目录

热门文章