文章目录
6.1 关系代数
关系代数的基本运算有:选择,投影,并,集合差,笛卡尔积,更名
除了基本运算以外,还有一些其他运算:集合交,自然连接和赋值
6.1.1 基本运算
选择,投影和更名对一个关系进行运算,因此称为一元运算
其它的称为二元运算,对两个关系进行运算
1.选择运算
选择运算选出满足特定条件的元组,使用符号σ来表示选择

比如

例:查找年龄不小于20岁的男学生

通常,我们还可以使用=,<,> 等逻辑连接词作为过滤的条件
2.投影运算
投影用大写希腊字母Π(PI)表示,从关系的若干列中取若干列得到一个新的关系。
注意:投影的结果自动去重

例:查询所有学生的姓名和年龄
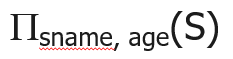
例:查询001号学生所选修的课程号
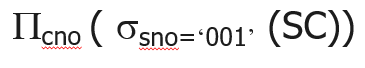
3.关系运算的组合
关系运算的组合即将多个代数运算组合成一个关系代数表达式
4.并运算
并运算:获取所有至少出现在两个关系之一的元组集合
注意:两个关系R与S若进行并运算,则它们一定是相容的
相容:
- 关系R与S的属性数目必须相同(列数相同)
- 对 ∀i,R中第i个属性的域必须和S的第i个属性的域相同
比如以下两个关系做并运算的结果

例:查询选修了c1号或c2号课程的学生学号

5.集合差运算
差运算:求出所有出现在一个关系而不再另一关系中的元组集合
注意:两个关系必须是相容的
比如:

6.笛卡尔积运算
笛卡尔积用”x“表示,可以将任意两个关系的信息组合组合在一起。将关系r1和关系r2的笛卡尔积写作 r1 x r2
例:没有重名列的情况

有重名列的情况

运算结果的命名:关系名.属性名
例:查询软件学院学生的选课情况
要求写出关系模式:(sno,sname,cno,score)

结果为:
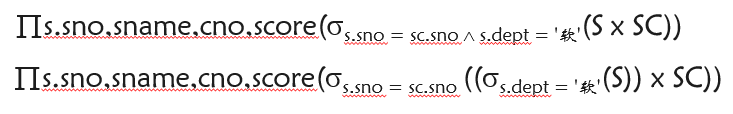
7.更名运算
(1)将名字x赋给关系表达式E的运算结果
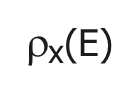
(2)将名字x赋给关系表达式E的运算结果,并将各属性名改为A1,A2,A3…
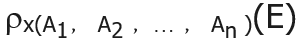
例:查询数学成绩比王红同学高的学生姓名
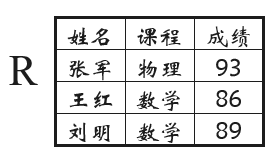
结果:

例:基于关系customer(name,street,city),实现下列查询:查询所有与smith居住在同一城市同一街道的客户

从父子关系表

(1)查询祖孙关系
这里的p表示parent表
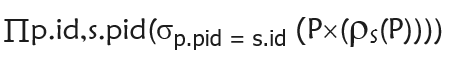
(2)查询三代以内的祖孙关系
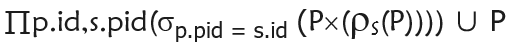
6.1.2 关系代数的形式化定义
关系代数中一般的表达式都是由更小的子表达式构成的,假设E1,E2都是关系代数表达式
则以下都是关系代数表达式
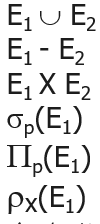
6.1.3 附加的关系代数运算
1.集合交运算
直接上例子

例:查询同时选修了c1号和c2号的学生学号
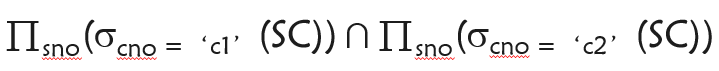
2.Θ连接(了解)
定义:从两个关系的笛卡尔积中选取给定属性间满足一定条件的元组

A,B位R和S上度数相等且可比的属性集合
Θ为比较运算符,当Θ为等号时称为等值连接
例:

3.自然连接运算
从两个关系的笛卡尔积中选取在相同属性列B上取值相等的元组,并去掉重复的属性
比如:

例:查询001号学生所在院系的编号和名称
由于学生表和院系表中都有dno这个属性,因此采用自然连接即可
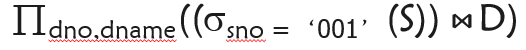
多个属性自然连接

4.除运算
象集的概念

举例:

除法的概念

例1:
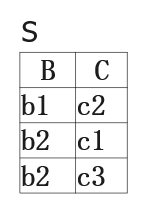
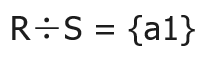
例2:

此时:
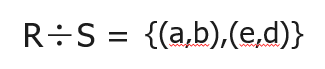
例3:查询选修了全部课程的学生的学号
使用除运算:

不使用除运算:
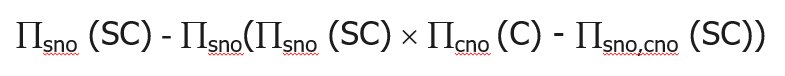
例4:查询至少选修了c1和c2课程的学生学号
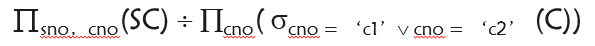
5.赋值运算(了解,用得比较少)
有时通过给临时关系变量赋值的方法来写关系代数表达式会很方便

例:

6.外连接运算
外连接是对连接运算的扩展,可以处理空值的情况
外连接与自然连接运算相似,不同之处在于它在结果中创建带空值的元组,以保留在连接中丢失的那些元组
左外连接,右外连接和全外连接:

例:左外连接的结果

例:右外连接的结果

例:全外连接的结果

6.1.4 扩展的关系代数运算
1.广义投影(了解)
定义:投影列表中使用算数表达式对投影进行拓展
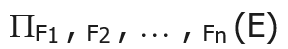
例:
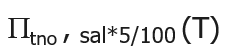
这里使用了 sal*5/100 这个算数表达式
2.聚集函数
(1)求和函数sum( )
例:

(2)计算平均值:avg( )

(3)计算最大值:max( )
(4)计算最小值:min( )

(5)计数:count( )

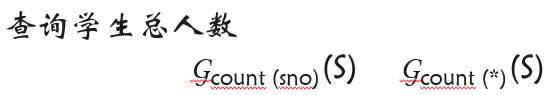

(6)分组函数
将一个关系中的元组分为若干组,对每一组使用聚集函数
格式:

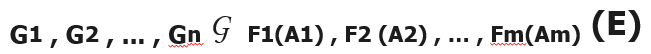
Gi是用于分组的属性,Fi是聚集函数,Ai是属性名
例:

6.2 元组关系演算
元组关系演算是非过程化的查询语言。它只描述所需信息,而不给出获得该信息的具体过程
元组关系演算种的查询表达式为:{ t | P ( t ) }
表示使谓词P为真的元组t的集合
用t[A]表示元组t在属性A上的值
用t∈R表示元组t在关系R中
常用表达式:

6.2.1 查询示例
例1:

例2:

例3:

对于关系:S(sno,sname,sex,age,dno)

6.2.2 形式化定义

例:查询d1学院或者选修了c1课程的学生学号(两张表以上查询)
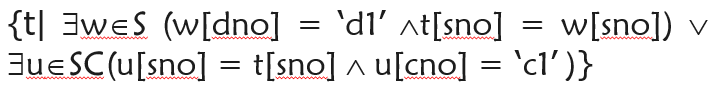
例:查询软件学院老师的姓名

例:查询未选课的学生姓名

例:查询选修了002号学生选修的全部课程的学生学号


6.2.3 表达式的安全性
元组关系演算有可能会产生无限关系,这样的表达式是不安全的
如{t | ┑(t ∈ R)},求所有不在R中的元组,这样的表达式就会产生无穷多的元组
引入公式P的域概念,用dom§表示

例:
