A. Will he Die?
题意: 给定一个坐标轴和 n , m n,m n,m,初始位置为零点,每秒都有 1 2 \frac{1}{2} 21的概率向左或者向右移动,求在 m m m秒内走到 n n n点的概率

分析: 组合数学+费马小定理求逆元
一共有 m m m秒,故而有 2 m 2^m 2m种移动方案。
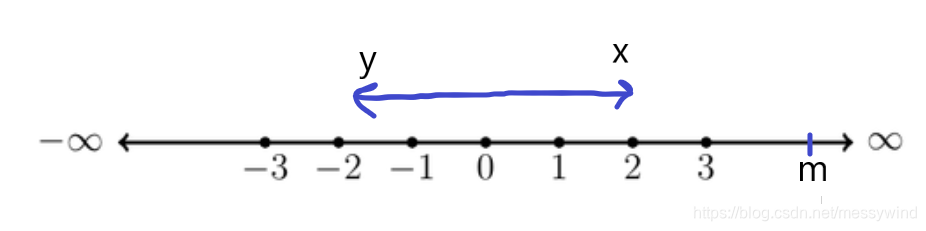
假设向着 m m m点走了 x x x,背离 m m m点走了 y y y,那么有
{ x + y = n x − y = m \left\{\begin{matrix} x+y=n\\ x-y=m \end{matrix}\right. {
x+y=nx−y=m
解出 x = m + n 2 x=\frac{m+n}{2} x=2m+n
所以移动到m点的方案总数为 C m m + n 2 C^{\frac{m+n}{2}}_{m} Cm2m+n
故而总的概率为
C m m + n 2 2 m \frac{C^{\frac{m+n}{2}}_{m}}{2^{m}} 2mCm2m+n
题目要求我们 m o d 1 0 9 + 7 \mod10^9+7 mod109+7 ,所以要用费马小定理求逆元
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int mod=1e9+7,N=2e5+5;
LL t,n,m,fact[N],infact[N];
LL qmi(LL a,LL b){
LL res=1;
while(b){
if(b&1) res=res*a%mod;
a=a*a%mod;
b>>=1;
}
return res;
}
int main(){
fact[0]=infact[0]=1;
for(LL i=1;i<N;i++) fact[i]=fact[i-1]*i%mod,infact[i]=infact[i-1]*qmi(i,mod-2)%mod;
cin>>t;
while(t--){
cin>>n>>m;
if(abs(n)%2!=m%2||abs(n)>m) cout<<0<<endl;
else cout<<fact[m]*infact[m+n>>1]%mod*infact[m-(m+n>>1)]%mod*qmi(qmi(2,m),mod-2)%mod<<endl;
}
}
B. Ran and the Lock Code
题意: 给定 n , a n,a n,a,求最多有多少个不同的数 x i x_i xi,使得 a = ∑ i = 1 n x i n a=\frac{\sum_{i=1}^{n}x_i }{n} a=n∑i=1nxi
分析: 二分
假设二分的答案为 m i d mid mid,由贪心思想可知这些不同的数必定为首项为 1 1 1,公差为 1 1 1的等差数列,那么只需要判断 n − m i d + n-mid+ n−mid+前 m i d mid mid项和能不能平均成 a a a,二分最大的边界即可。
式子: m i d ( m i d + 1 ) 2 + n − m i d ≤ a ∗ n \frac{mid(mid+1)}{2}+n-mid\le a*n 2mid(mid+1)+n−mid≤a∗n
整理:
2 ∗ n − m i d ≤ 2 ∗ a ∗ n − m i d ∗ m i d 2*n-mid\le 2*a*n-mid*mid 2∗n−mid≤2∗a∗n−mid∗mid
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
LL n,a,t;
int main(){
cin>>t;
while(t--){
cin>>n>>a;
LL l=1,r=n;
while(l<=r){
LL mid=l+r>>1;
if(2*n-mid<=2*a*n-mid*mid) l=mid+1;
else r=mid-1;
}
cout<<l-1<<endl;
}
}
C. Professor Agasa Lab
题意:
你有以下等式:
y = ( x ∗ a − b ) m o d m y=(x*a-b)\mod m y=(x∗a−b)modm
如果你知道 y , a , b y,a,b y,a,b的值,计算 x x x
x = ( y − b ) ∗ a − 1 m o d m x=(y-b)*a^{-1}\mod m x=(y−b)∗a−1modm
其中 a − 1 a^{-1} a−1是 a a a的逆元,当 gcd ( a , m ) ≡ 1 \gcd(a,m)\equiv1 gcd(a,m)≡1时逆元存在。
分析: 数论+筛法求欧拉函数+找规律
找规律发现最后的结果是 1 ∼ n 1\sim n 1∼n中与 n n n互质的个数乘互质数的最大值
前半部分是欧拉函数,后半部分显然就是 n − 1 n-1 n−1,因为相邻两个数一定互质。
代码:
#include<stdio.h>
using namespace std;
const int N=1e6;
typedef long long LL;
LL n,primes[N],euler[N],cnt,t;
bool st[N];
void get_eulers(int n){
euler[1]=1;
for(int i=2;i<=n;i++){
if(!st[i]){
primes[cnt++]=i;
euler[i]=i-1;
}
for(int j=0;primes[j]<=n/i;j++){
int t=primes[j]*i;
st[t]=1;
if(i%primes[j]==0){
euler[t]=primes[j]*euler[i];
break;
}
euler[t]=(primes[j]-1)*euler[i];
}
}
}
int main(){
get_eulers(N);
scanf("%lld",&t);
while(t--){
scanf("%lld",&n);
printf("%lld\n",(n-1)*euler[n]);
}
}
G. Preparing for Exams
题意: 已知 k , l , m , n k,l,m,n k,l,m,n,求 x , y x,y x,y, k = o d , l = o a , m = S Δ o d a , n = S Δ o b c k=od,l=oa,m=S_{Δoda},n=S_{Δobc} k=od,l=oa,m=SΔoda,n=SΔobc
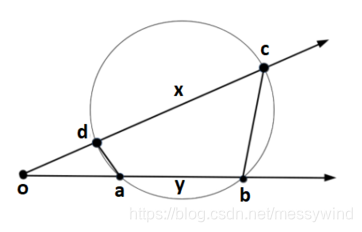
分析:
由圆幂定理得:
k ∗ ( k + x ) = l ∗ ( y + l ) ⋯ ① k*(k+x)=l*(y+l)\cdots① k∗(k+x)=l∗(y+l)⋯①
由正弦定理得:
S Δ o d a = m = 1 2 ∗ k ∗ l ∗ sin∠doa S_{Δoda}=m=\frac{1}{2}*k*l*\text{sin∠doa} SΔoda=m=21∗k∗l∗sin∠doa
sin∠doa = 2 n l + y k + x ⋯ ② \text{sin∠doa}=\frac{\frac{2n}{l+y}}{k+x}\cdots② sin∠doa=k+xl+y2n⋯②
带入 ① ② ①② ①②得 y = n ∗ k 2 m − l ⋯ ③ y=\sqrt{\frac{n*k^2}{m}}-l\cdots③ y=mn∗k2−l⋯③
将 ③ ③ ③带入 ① ① ①得 x = l ∗ ( y + l ) k − k x=\frac{l*(y+l)}{k}-k x=kl∗(y+l)−k
代码:
#include<bits/stdc++.h>
using namespace std;
int t;
double k,l,m,n;
int main(){
scanf("%d",&t);
while(t--){
scanf("%lf%lf%lf%lf",&k,&l,&m,&n);
double y=sqrt(n*k*k/m)-l;
printf("%lf ",y);
printf("%lf\n",l*(y+l)/k-k);
}
}
H. Genta Game
题意: 给定一个长度为 n n n的字符串和 q q q和询问,每次询问将下标为 p p p的字符修改为 c c c,统计每次询问的回文串。
分析: O ( 1 ) O(1) O(1)维护对称串相等的个数。如果修改之前不相等,修改之后相等,那么总个数 + 1 +1 +1,否则不加。如果修改之前相等,修改之后不相等,那么总个数 − 1 -1 −1。每次判断总个数是否为 n / 2 n/2 n/2
代码:
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N=1e5+5;
int t,n,q,p;
char c,s[N];
int main(){
cin>>t;
while(t--){
LL res=0,cnt=0;
cin>>n>>q>>s+1;
for(int i=1;i<=n/2;i++){
if(s[i]==s[n-i+1]) cnt++;
}
while(q--){
int flag=0;
cin>>p>>c;
if(s[p]==c&&cnt!=n/2) continue;
if(s[p]!=s[n-p+1]) flag=1;
s[p]=c;
if(s[p]==s[n-p+1]){
if(cnt<n/2) cnt++;
if(cnt==n/2) res++;
}
else if(flag){
}
else cnt--;
}
cout<<res<<endl;
}
}