线性代数笔记 [3] —— 从增广矩阵漫谈矩阵转置对向量在四个向量子空间内的“飞舞”（第三篇）

文章转载请注明出处，加上原文地址链接，谢谢！
https://blog.csdn.net/weixin_46959681/article/details/105739995

---

---

前言

该篇文章以非齐次线性方程组例题引出增广矩阵(A,b)的解集，配合矩阵的QR分解对增广矩阵(A,b)重新构造。在转置方面从代数的角度切入，但这个角度比较浅显。我们需要真正明白的是转置在向量空间层面发挥了什么作用。重要提醒，在阅读该文章之前，必须将MIT线性代数习题公开课第11题的习题观看完毕并消化理解，这是串联所有知识点的脉络，其余只是模块组成。

---

增广矩阵(Augmented matrix)

e.g. 求出非齐次方程组的通解

$$\{\begin{array}{c}{x}_1+2x_2=3\\ 2x_1+4x_2=6\end{array}$$

解： 特解

$$X^{\ast }=\left(\begin{array}{c}1\\ 1\end{array}\right)$$

零解

N ( A ) = { c ( − 2 1 ) ∣ c ∈ R } N(A)=\lbrace c\begin{pmatrix}-2\\1\\ \end{pmatrix} |c\in R\rbrace N(A)={ c(−21​)∣c∈R}

故原方程组解集为
S ( A , b ) = { ( 1 1 ) + c ( − 2 1 ) ∣ c ∈ R } S(A,b)=\lbrace \begin{pmatrix}1\\1\\\end{pmatrix}+c\begin{pmatrix}-2\\1\\\end{pmatrix}|c \in R \rbrace S(A,b)={ (11​)+c(−21​)∣c∈R}

可以看出任意解都可以被分解成特解和零解。

那么对于线性方程组$x_1{a}_1+\cdots +x_n{a}_n=\beta$有解到底意味着什么呢？结合本人第二篇博文，我们对于方程式

$$x_1{a}_1+\cdots +x_n{a}_n=\beta$$

有解可以获得以下结论：

1. $\beta \in (a_1,a_2,\dots ,a_n)$
2. $(a_1,a_2,\dots ,a_n,\beta )\subseteq (a_1,a_2,\dots ,a_n)$
3. $(a_1,a_2,\dots ,a_n,\beta )=(a_1,a_2,\dots ,a_n)$
4. $dim(a_1,a_2,\dots ,a_n,\beta )=dim(a_1,a_2,\dots ,a_n)$
5. $rank(a_1,a_2,\dots ,a_n,\beta )=rank(a_1,a_2,\dots ,a_n)$

（以上几条结论可互相推导。）

对于增广矩阵，有以下结构图：

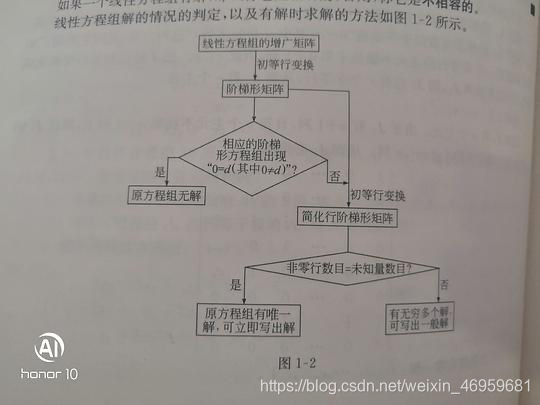
（高等代数学习指导书（第二版上册）第14页）

---

｜从QR分解的角度重构增广矩阵

首先我们来看一下什么是QR分解。

定理 如果 $\mathsf{m}\times \mathsf{n}$ 矩阵 $\mathsf{A}$ 的列线性无关，那么A可以分解为$A=QR$，其中$Q$是一个$m\times n$矩阵，其列形成$ColA$的一个标准正交基，R是一个$n\times n$上三角矩阵且在对角线上的元素为正数。若Q是一个方阵，则$Q^{-1}=Q^T$，Q为正交阵。令$Q=(q_1,\dots ,q_n)$，故
$$Q^{T}Q=\left(\begin{array}{c}{q}_1^T\\ ⋮\\ q_n^T\end{array}\right)\left(\begin{array}{ccc}{q}_1& \dots & q_n\end{array}\right)={\left(\begin{array}{cccc}1& 0& \cdots & 0\\ 0& 1& \cdots & 0\\ ⋮& ⋮& \ddots & ⋮\\ 0& 0& \cdots & 1\end{array}\right)}_{n\times n}=I_n$$

应用方面：

1. 设 A 为 $m\times n$ 阶矩阵，A 的列向量线性无关，$A=QR$。$Ax=b\iff A^{T}A\hat{x}=A^{T}b\iff R^T{Q}^{T}QR\hat{x}=R^T{Q}^{T}b\iff R^{T}R\hat{x}=R^T{Q}^{T}b\iff R\hat{x}=Q^{T}b\iff \hat{x}=R^{-1}{Q}^{T}b$。其中，若$A$的列相互正交，$A=（a_1,\dots ,a_n）$，则$R=diag(\parallel a_1\parallel ,\dots ,\parallel a_n\parallel )\to \hat{x}=R^{-1}{A}^{T}b$。设$Ax=b$无解，则$b$在$C(A)$上的投影为

$$\mathsf{P}=\sum _{i=1}^n(\frac{a_i^{T}b}{a_i^T{a}_i})a_i$$

3. $A$是可逆矩阵，则QR分解唯一。
4. 设$A_{m\times n}$列满秩，有$A=QR,b\notin C(A)$，设其投影在$C(A)$为$P，e=b-p$，则$(A,b)$为列满秩，其QR分解为 $$(\mathsf{A},\mathsf{b})=(\mathsf{Q},\frac{\mathsf{e}}{\parallel \mathsf{e}\parallel })\left(\begin{array}{cc}R& \alpha \\ 0& \parallel e\parallel \end{array}\right),\alpha ={\mathsf{Q}}^{\mathsf{T}}\mathsf{b}$$，$\mathsf{A}=({\mathsf{a}}_1,\dots ,{\mathsf{a}}_{\mathsf{n}})\sim \mathsf{Q}=({\mathsf{q}}_1,\dots ,{\mathsf{q}}_{\mathsf{n}})$

上述从基的角度细细的梳理了QR分解，请多看几遍并配合相关题目理解。

---

转置（Transpose）

定义 设A为$\mathsf{m}\times \mathsf{n}$阶矩阵，第$i$行$j$ 列的元素是$\mathsf{a}(\mathsf{i},\mathsf{j})$，即：$A=(a_{ij}{)}_{m\times n}$，把$m\times n$矩阵A的行换成同序数的列得到一个$\mathsf{n}\times \mathsf{m}$矩阵，此矩阵叫做A的转置矩阵，记做${\mathsf{A}}^{\mathsf{T}}=({\mathsf{a}}_{\mathsf{j}\mathsf{i}}{)}_{\mathsf{n}\times \mathsf{m}}$。

代数式表达：$\mathsf{A}=({\mathsf{a}}_{\mathsf{i}\mathsf{j}}{)}_{\mathsf{m}\times \mathsf{n}}<\mathsf{f}:\mathsf{T}>{\mathsf{A}}^{\mathsf{T}}=({\mathsf{a}}_{\mathsf{j}\mathsf{i}}{)}_{\mathsf{n}\times \mathsf{m}}$

绝大多数人运算的时候也只是在计算稿上将矩阵沿主对角线进行翻转，如$A=\left(\begin{array}{cc}1& 2\\ -2& 1\end{array}\right)$转置有$A^T=\left(\begin{array}{cc}1& -2\\ 2& 1\end{array}\right)$。我们再从代数层面深入一点，来看下面两个运算。

e.g. $A\in F^{m\times n}$，$X\in F^{n\times 1}$，$B\in F^{n\times p}$，则

$(Ax{)}^T=(x_1{A}_1+\cdots +x_n{A}_n{)}^T=x_1{A}_1^T+\cdots +x_n{A}_n^T=\left(\begin{array}{cccc}{x}_1& x_2& \cdots & x_n\end{array}\right)\left(\begin{array}{c}{A}_1^T\\ A_2^T\\ ⋮\\ A_n^T\end{array}\right)=x^T{A}^T$ （数$x$转置仍然为$x$。）

e.g.$(AB{)}^T=(A{B}_1,A{B}_2,\cdots ,A{B}_P{)}^T=\left(\begin{array}{c}(A{B}_1{)}^T\\ ⋮\\ (A{B}_p{)}^T\end{array}\right)=\left(\begin{array}{c}{B}_1{A}^T\\ ⋮\\ B_p^T{A}^T\end{array}\right)=\left(\begin{array}{c}{B}_1^T\\ ⋮\\ B_p^T\end{array}\right)A^T=B^T{A}^T$

笔者在这里可以肯定，绝大多数人对转置的认知都停留在以上定义层面以及上述的代数运算层面。那转置在几何层面起什么作用呢？容笔者在这埋下一个伏笔，下面我们来快速的过一遍向量子空间。

---

向量子空间（subspace）

（笔者清华线性代数公开课笔记第一部分第27页）

四个基本子空间的基的代数表达：

• 列空间(Column space) C ( A ) = { y ∈ R m ∣ y = A x , ∃ X ∈ R N } C(A)=\lbrace y\in R^m | y=Ax,\exists X\in R^N\rbrace C(A)={ y∈Rm∣y=Ax,∃X∈RN}
• 左零空间(Left nullspace) N ( A T ) = { x ∈ R m ∣ x T A = 0 } N(A^T)=\lbrace x\in R^m | x^TA=0\rbrace N(AT)={ x∈Rm∣xTA=0}
• 零空间(Nullspace) N ( A ) = { x ∈ R n ∣ A x = 0 } N(A)=\lbrace x\in R^n | Ax=0\rbrace N(A)={ x∈Rn∣Ax=0}
• 行空间(Row space) C ( A T ) = { y ∈ R n ∣ y = A T x , ∃ X ∈ R m } C(A^T)=\lbrace y\in R^n | y=A^Tx, \exists X \in R^m\rbrace C(AT)={ y∈Rn∣y=ATx,∃X∈Rm}

小贴士：在学习的数学的过程你需要很多固定的元认知模块，以便在学习的过程中像搭积木一样随取随用。比如上面四个子空间的代数表达式，心里知道核心图仅是第一步，第二步更重要，将其用数学语言代数化表达出来，这对于任何一个科目的学习都是通用的。类似的还有数乘，加法，乘法等。（如果有个“仓库”随时进行查找，也没有问题。）

---

以MIT线性代数习题公开课第11题为串联脉络

在开始阅读之前，请确保你已经看完MIT线代习题公开课第11题，而且有了略微的理解。

（笔者2019.11.30的线代习题公开课摘录笔记第7页）

在计算的过程中，我们已经的得到了四个子空间的基底，下一步我们来看它是如何经过转置产生联系的。（直接上图）

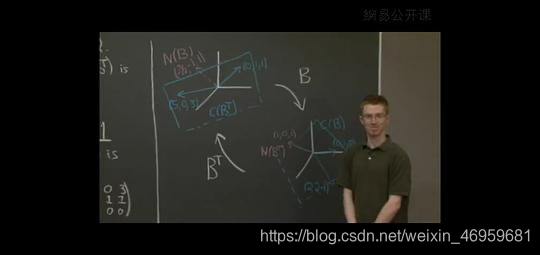
习题公开课视频的讲解非常清晰，行空间（基底 { ( 5 0 3 ) , ( 0 1 1 ) } \lbrace \begin{pmatrix}5\\0\\3\\\end{pmatrix},\begin{pmatrix}0\\1\\1\\\end{pmatrix}\rbrace { ⎝⎛​503​⎠⎞​,⎝⎛​011​⎠⎞​}）和零空间（基底 { ( − 3 5 − 1 1 ) } \lbrace \begin{pmatrix}-\frac{3}{5}\\-1\\1\\\end{pmatrix}\rbrace { ⎝⎛​−53​−11​⎠⎞​}）经过转置被投射到列空间（基底 { ( 1 − 2 1 ) , ( 0 1 0 ) } \lbrace \begin{pmatrix}1\\-2\\1\\\end{pmatrix},\begin{pmatrix}0\\1\\0\\\end{pmatrix}\rbrace { ⎝⎛​1−21​⎠⎞​,⎝⎛​010​⎠⎞​}）和左零空间（基底 { ( 1 0 1 ) } \lbrace \begin{pmatrix}1\\0\\1\\\end{pmatrix} \rbrace { ⎝⎛​101​⎠⎞​}）。在这里可以清晰明了的看到矩阵的数值计算仅仅是流于表面的现象，向量空间与向量空间之间经由转置发生的变化才是真正的核心。

小贴士：引申一个问题，向量“$\nearrow$”究竟是什么？经过以上的讲解，再将其理解为有方向、有长度的箭头是否已经有点太“低端”了呢？你必须理解，初次学习线性代数，引入一个“有方向、有长度的箭头”作为向量仅仅是为了让你建立几何直观方便入门，在学习的过程中，你要逐渐摒弃这个概念，真正从空间变化的角度来理解线性变换。更多时候，你要把向量看作是空间变化的线性载体。（观点启蒙于课程「线性代数的本质」）

---

参考资料

1. 北京航空航天大学线性代数公开课李尚志老师&个人笔记
2. 线性代数的本质系列课程个人笔记第2页
3. 清华大学线性代数公开课第一部分徐帆老师&马辉老师 个人笔记第7页、第32页
4. MIT线性代数习题公开课个人笔记 第11页
5. 高等代数学习指导书（第二版上册）邱维声著 第14页

---

文章更新记录

• 文章版面微微调整，修改了几个错别字以及数学符号样式调整。「2020.12.4 星期五 15:22」
• 文章调整。 「2021.4.2 18:58」