目录
0. 单时间常数RC电路的频率响应
(1) RC高通电路
电路图
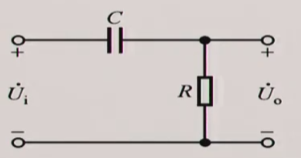
增益
$$
$$
② 相频响应
$$
$$
曲线分析
- 当
- 当
- 当
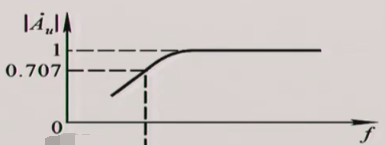
③ 幅频响应
$$
$$
曲线分析
- 当
- 当
- 当
(2) RC低通电路
① 传输特性
A ˙ u = U ˙ o U ˙ i = 1 1 + 1 j ω R C \dot{A}_u = \frac{\dot{U}_o}{\dot{U}_i} = \frac{1}{1+\frac{1}{j\omega RC}} A˙u=U˙iU˙o=1+jωRC11
下限截止频率 f L = 1 2 π R C f_L = \frac{1}{2\pi RC} fL=2πRC1
② 幅频特性
∣ A ˙ u ∣ = 1 1 + ( f f H ) 2 |\dot{A}_u| = \frac{1}{\sqrt{1+(\frac{f}{f_H})^2}} ∣A˙u∣=1+(fHf)21
曲线分析
- 当 f < f H f<f_H f<fH 时，
- 当 f = f H f=f_H f=fH 时，
- 当 f > f H f>f_H f>fH 时，
③ 相频响应
ϕ h = − a r c t a n ( f f H ) \phi_h= -arctan(\frac{f}{f_H}) ϕh=−arctan(fHf)
曲线分析
- 当 f < f H f<f_H f<fH 时，
- 当 f = f H f=f_H f=fH 时，
- 当 f > f H f>f_H f>fH 时，
1. 低频响应
(1) 共射放大电路
(2) 共源放大电路
2. 高频响应
(1) 共射放大电路
分析步骤
- 根据BJT混合 π \pi π形高频小信号模型，画等效电路
- 求密勒电容，再次等效，把电容单向化
- 根据电容间的关系，再次简化，
- 利用戴维宁等效电路进行简化
- 求解高频响应和上限频率。