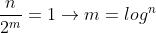【数据结构】——查找算法：顺序查找、二分查找

一、in查找

  最简单（low)的查找算法：for i in range(3)

二、顺序查找

1.无序列表

顺序查找的时间复杂度较高为O（n）
  若要查找的元素在列表中有多个，则在查找到第一个后即停止

时间复杂度：

  最好：O（1）最好即第一个元素就是目标元素当不存在要查找的元素时为O（n）
  最坏：O（n）最坏是查到最后一个才找到目标元素

#无序列表的顺序查找
m=[1,5,3,9,7]
def seqSearch(alist,item):
    i=0
    found=False
    while i<len(alist) and not found:
        if alist[i]==item:
            found=True
        else:
            i+=1
    return found
seqSearch(m,2)
>>False

2.有序列表

  加入一个停止条件：当前列表中元素大于要查找元素时即停止，不再继续查找

#有序列表的顺序查找
m=[1,3,5,7,9]
def seqSearch(alist,item):
    i=0
    found=False
    stop=False#停止判断器，当前列表中元素大于要查找元素时停止
    while i<len(alist) and not found and not stop:#未找到且未达到停止条件
        if alist[i]==item:
            found=True
        else:
            if alist[i]>item:
                stop=True
            else:
                i+=1
    return found
seqSearch(m,2)
>>False

时间复杂度：

  最好：O（1）最好即第一个元素就是目标元素，或第一个元素大于要查找的元素，列表中不存在目标元素
  最坏：O（n）最坏是查到最后一个才找到目标元素或目标元素大于列表中最后一个元素，列表中不存在目标元素

三、二分查找

  假设列表是有序升序列表:

1. 取出列表中间位置的元素与目标元素比较，若相等，则查找成功
2. 若中间元素大于目标元素，则取出中间元素之前的所有元素作为前子列表，在前子列表中进行查找；
3. 若中间元素小于目标元素，则取出中间元素之后的所有元素作为后子列表，在后子列表中进行查找。
4. 如此重复，直到查找到目标元素，则查找成功，若直到子列表不存在仍没有找到目标元素，则查找不成功。

#二分查找
m=[1,3,5,7,9]
def binarysearch(alist,item):
    if len(alist)==0:#当子列表不再存在时，返回False
        return False
    else:
        mid=len(alist)//2#取出中间元素
        if alist[mid]==item:#如果目标元素=中间元素
            return True
        else:
            if item<alist[mid]:#目标元素小于中间元素，取出前子列表进行递归
                return binarysearch(alist[:mid],item)
            else:
                return binarysearch(alist[mid+1:],item)
binarysearch(m,2)
>>False

时间复杂度：

  最好：O（1）

  最坏：O（logn）