1.什么是感知机
根据输入实例的特征向量X对其进行二分类的线性分类模型
2.目标
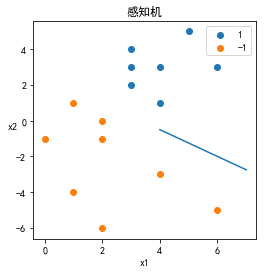
感知机模型从输入空间到输出空间的映射可表示为y=f(x)=sign(w*x+b),感知机学习的目的就是学得一个使训练样本正例与负例完全正确分开的超平面wx+b=0,也就是学习参数w和b。
3.损失函数
用分类错误的样本到超平面的距离表示。
点到平面的距离公式为:
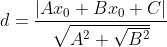
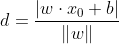
因为在函数y=f(x)=sign(w x+b)中sign为符号函数,因此当wx+b≥0时,y=1;当w*x+b≤ 0时,y=-1;因此对于任意分类错误的样本,其一定满足以下式子:
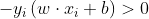
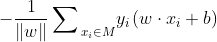
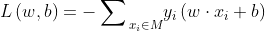
4.梯度下降法
通俗的说,所谓梯度,就是导数和偏导数。梯度下降法的思想就是:梯度方向是目标函数值下降最快的方向,因此沿着梯度下降的方向优化能最快寻找到目标函数的极小值。
下边这张图,直观展示了在只考虑一个参数w时的梯度下降原理:
因此参数w、b的更新可表示为:
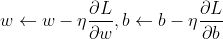
在感知机中采用随机梯度下降法,即每次随机选择一个分类错误的样本计算其梯度,进行w和b的更新,即:
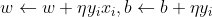
根据w、b的更新公式可以看出感知机学习的过程即利用梯度对参数进行更新,从而使损失函数更小。其过程直观理解为:当一个样本被当前超平面划分到分类错误一类时,利用此样本调整超平面的参数,使超平面向靠近该样本的方向移动,则该样本距离超平面的距离减小,从而降低损失函数,直到超平面移动至使该样本被正确划分为止。
5.感知机算法伪代码

6.sklearn实现感知机算法
首先导入需要的包:
import sklearn
import pandas as pd
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Perceptron
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
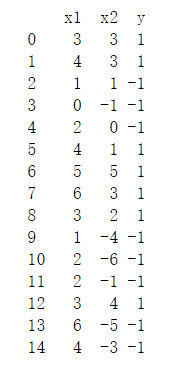
导入数据:这里的数据集是一份包含两维特征、15个样本的线性可分数据。
a=pd.read_excel('D:/DataMining/sj/gzjyb.xlsx',header=0)
print(a)
X=a.iloc[:,:2]
y=a.iloc[:,-1]
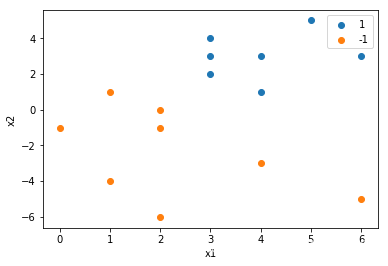
数据如下所示:
plt.scatter(a[(a['y']==1)]['x1'], a[(a['y']==1)]['x2'], label='1')#绘制出标签为1的样本
plt.scatter(a[(a['y']==-1)]['x1'], a[(a['y']==-1)]['x2'], label='-1')
plt.xlabel('x1')
plt.ylabel('x2')
plt.legend()
数据可视化结果为:
pct= Perceptron(fit_intercept=True, max_iter=10, shuffle=True)#利用sklearn的Perceptron训练模型
pct.fit(X, y)
print(pct.coef_)#输出w
print(pct.intercept_)#输出b
>>[[2. 3.]]
>>[-6.]
至此我们就得到了Perceptron给出的超平面为:
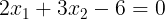
plt.figure(figsize=(4,4))
#画出样本点
plt.scatter(a[(a['y']==1)]['x1'], a[(a['y']==1)]['x2'], label='1')
plt.scatter(a[(a['y']==-1)]['x1'], a[(a['y']==-1)]['x2'], label='-1')
# 画出超平面
x_ponits = np.arange(0,8)
y_ = -(pct.coef_[0][0]*x_ponits + pct.intercept_)/pct.coef_[0][1]# 超平面公式x2=-(w1x1+b)/w2
plt.plot(x_ponits, y_)
# 图示
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False#设置中文标题
plt.title('感知机示例')
plt.xlabel('x1',rotation='horizontal')
plt.ylabel('x2',rotation='horizontal')
plt.legend()
上述过程是在全部样本上进行模型训练的,在此处再尝试划分训练集,计算其分类准确率:(这里样本过少,不具有代表性)
#划分数据集,计算准确率
X_train, X_test, y_train, y_test=train_test_split(X, y, test_size=0.1,stratify = y ,random_state=0)#样本太少了!!!
pct= Perceptron(fit_intercept=True, max_iter=10, shuffle=True)
pct.fit(X_train, y_train)#在训练集上生成模型
predicted_test= pct.predict(X_test)#在验证集上预测
print("准确率",accuracy_score(y_test,predicted_test))
>>准确率 1.0
7.python代码实现感知机算法
前半部分数据导入、可视化与6中同,在此不赘述,直接到模型:
class Model:
def __init__(self):
self.w = np.ones(a.shape[1]-1, dtype=np.float32)#创建浮点型、特征数量len(a[0])-1维数组作为初始w
self.b = 0
self.l_rate = 0.1
def sign(self, x, w, b):
y = np.dot(x, w) + b#定义超平面
return y
# 随机随机梯度下降
def fit(self, X, y):
wrong = False
while wrong is False:
wrong_count = 0
X=np.array(X)
y=np.array(y)
for d in range(len(X)):#每次取一个样本利用随机梯度下降更新wb
if y[d] * self.sign(X[d], self.w, self.b) <= 0:#如果为误分类样本,则用它更新
self.w = self.w + self.l_rate * np.dot(y[d], X[d])#更新w
self.b = self.b + self.l_rate * y[d]#更新b
wrong_count += 1#记录误分类样本数
if wrong_count == 0:#直到训练集中没有误分类样本,结束
wrong = True
return self.w,self.b,wrong_count
def score(self):
pass
训练模型:
pct= Model()
pct.fit(X,y)
>>(array([0.3, 0.4]), -0.9999999999999999, 0)
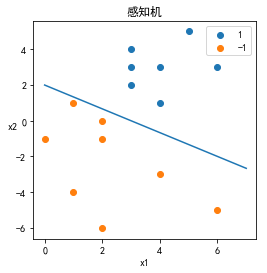
至此我们就得到了pct给出的超平面为:

结果可视化:
plt.figure(figsize=(4,4))
#画出样本点
plt.scatter(a[(a['y']==1)]['x1'], a[(a['y']==1)]['x2'], label='1')
plt.scatter(a[(a['y']==-1)]['x1'], a[(a['y']==-1)]['x2'], label='-1')
# 画出超平面
x_ponits = np.arange(0,8)
y_ = -(pct.w[0] * x_points + pct.b) / pct.w[1]
plt.plot(x_points, y_)
# 图示
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus'] = False#设置中文标题
plt.title('感知机')
plt.xlabel('x1',rotation='horizontal')
plt.ylabel('x2',rotation='horizontal')
plt.legend()
这是在学习机器学习过程中的学习笔记鸭,在学习过程中主要参考了李航老师的《统计学习方法》和一些大佬的代码。