LeetCode第四十八题—Python实现

---

title: LeetCode No.48

categories:

• OJ
• LeetCode

tags:

• Programing
• LeetCode
• OJ

---

LeetCode第四十八题

题目描述

给定一个 n × n 的二维矩阵 matrix 表示一个图像。请你将图像顺时针旋转 90 度。

你必须在 原地 旋转图像，这意味着你需要直接修改输入的二维矩阵。请不要 使用另一个矩阵来旋转图像。

示例 1：

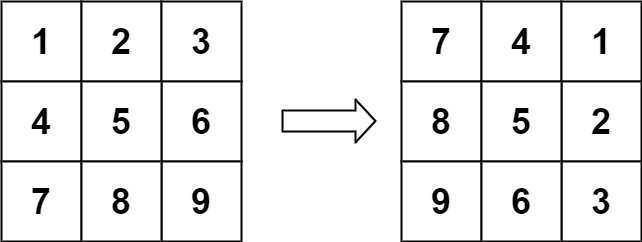
输入：matrix = [[1,2,3],[4,5,6],[7,8,9]]
输出：[[7,4,1],[8,5,2],[9,6,3]]

示例 2：

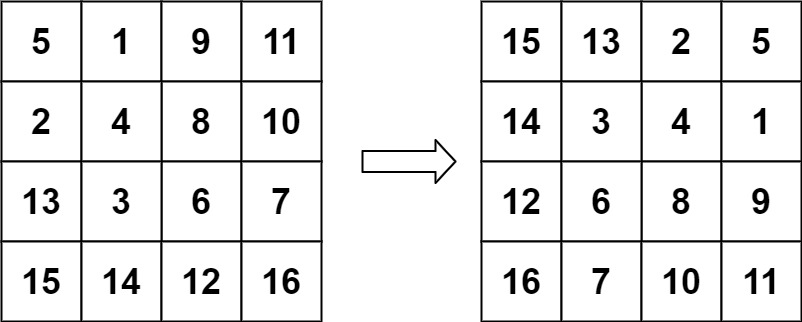
输入：matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]]
输出：[[15,13,2,5],[14,3,4,1],[12,6,8,9],[16,7,10,11]]
示例 3：

输入：matrix = [[1]]
输出：[[1]]
示例 4：

输入：matrix = [[1,2],[3,4]]
输出：[[3,1],[4,2]]

代码

class Solution(object):
    def rotate(self, matrix):
        """
        :type matrix: List[List[int]]
        :rtype: None Do not return anything, modify matrix in-place instead.

        核心思想:
                分析示例可以看出，我们如果先进性矩阵的转置，则可以得到目标结果的中心对称矩阵，然后在对该矩阵进行镜像
                即可以得到目标矩阵
        """
        n = len(matrix)
        # 先进行转置  行变列、列变黄
        for i in range(n):
            for j in range(n):
                # 仅进行对角交换即可
                if j > i:
                    t = matrix[i][j]
                    matrix[i][j] = matrix[j][i]
                    matrix[j][i] = t

        # 再进行镜像 中心轴对称变换
        center_axis = int(n/2) # 中心轴对应的下标
        for i in range(n):
            for j in range(n):
                if j < center_axis:
                    t = matrix[i][j]
                    matrix[i][j] = matrix[i][n-j-1]
                    matrix[i][n - j - 1] = t



if __name__ == '__main__':
    s = Solution()
    s.rotate(matrix = [[5,1,9,11],[2,4,8,10],[13,3,6,7],[15,14,12,16]])