督促自己——Java算法题四道——(深度优先搜索、回溯算法)
第一题:——回溯算法(中)
给定一个二维网格和一个单词,找出该单词是否存在于网格中。
单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水平相邻或垂直相邻的单元格。同一个单元格内的字母不允许被重复使用。
示例:
board =
[
[‘A’,‘B’,‘C’,‘E’],
[‘S’,‘F’,‘C’,‘S’],
[‘A’,‘D’,‘E’,‘E’]
]
给定 word = “ABCCED”, 返回 true
给定 word = “SEE”, 返回 true
给定 word = “ABCB”, 返回 false
基本思路:对每一个点都进行一次搜索,也就意味着有多条路径,只需要注意每条路径内不走已经走过的点就行了,只要一条路径走完还没结果就return,继续递归下一条路。
class Solution {
public boolean exist(char[][] board, String word) {
for(int i=0;i<board.length;++i){
for(int j=0;j<board[i].length;++j){
if(myexist(board,0,word,i,j)){
return true;
}
}
}
return false;
}
public boolean myexist(char[][]board,int count,String word,int x,int y){
if(count==word.length()){
return true;
}
if(x<0||x>=board.length||y<0||y>=board[0].length||board[x][y]!=word.charAt(count)){
return false;
}
board[x][y]='0';
boolean flag=myexist(board,count+1,word,x+1,y)||myexist(board,count+1,word,x,y+1)||myexist(board,count+1,word,x,y-1)||myexist(board,count+1,word,x-1,y);
board[x][y]=word.charAt(count);
return flag;
}
}
第二题:——回溯算法(中)
给定一个数字字符串 S,比如 S = “123456579”,我们可以将它分成斐波那契式的序列 [123, 456, 579]。
形式上,斐波那契式序列是一个非负整数列表 F,且满足:
0 <= F[i] <= 2^31 - 1,(也就是说,每个整数都符合 32 位有符号整数类型);
F.length >= 3;
对于所有的0 <= i < F.length - 2,都有 F[i] + F[i+1] = F[i+2] 成立。
另外,请注意,将字符串拆分成小块时,每个块的数字一定不要以零开头,除非这个块是数字 0 本身。
返回从 S 拆分出来的任意一组斐波那契式的序列块,如果不能拆分则返回 []。
示例 1:
输入:“123456579”
输出:[123,456,579]
示例 2:
输入: “11235813”
输出: [1,1,2,3,5,8,13]
示例 3:
输入: “112358130”
输出: []
解释: 这项任务无法完成。
基本思路:回溯思想,对所有可能的路依次递归遍历,直到找到第一个出现的斐波那契数列(此时必须字符串遍历完成,否则不作数)。如果结果不对,去除当前新插入顺序表中的数,回溯,进行下一条路的遍历。
class Solution {
public List<Integer> splitIntoFibonacci(String S) {
if(S==null||S.length()==0){
return new ArrayList<>();
}
List<Integer>list=new ArrayList<>();
splitInto(S,S,list,0);
return list;
}
public boolean splitInto(String s,String S,List<Integer>list,int index){
if(s==null||s.length()==0){
if(S.length()==index&&list.size()>=3){
return true;
}
return false;
}
for(int i=0;i<s.length();++i){
String str=s.substring(0,i+1);
if(str.length()>1&&str.charAt(0)=='0'){
break;
} else{
if(Long.valueOf(str)>Integer.MAX_VALUE){
break;
}
int len=list.size();
if(len>=2&&Integer.valueOf(str)>list.get(len-1)+list.get(len-2)){
break;
}
if(len<=1||list.get(len-1)+list.get(len-2)==Integer.valueOf(str)){
list.add(Integer.valueOf(str));
System.out.println(Integer.valueOf(str));
if(splitInto(s.substring(i+1,s.length()),S,list,index+str.length())){
return true;
}
list.remove(list.size()-1);
}
}
}
return false;
}
}
第三题:——深度优先搜索
有 n 个城市,其中一些彼此相连,另一些没有相连。如果城市 a 与城市 b 直接相连,且城市 b 与城市 c 直接相连,那么城市 a 与城市 c 间接相连。
省份 是一组直接或间接相连的城市,组内不含其他没有相连的城市。
给你一个 n x n 的矩阵 isConnected ,其中 isConnected[i][j] = 1 表示第 i 个城市和第 j 个城市直接相连,而 isConnected[i][j] = 0 表示二者不直接相连。
返回矩阵中 省份 的数量。
基本思路:分别对每个省(i)进行判断,如果还未被访问过,就省份加加,递归附属省(i,j)。切记对访问过的省标记一下。
class Solution {
int len=0;
public int findCircleNum(int[][] isConnected) {
for(int i=0;i<isConnected.length;++i){
if(isConnected[i][i]>0){
len++;
find(isConnected,i);
}
}
return len;
}
public void find(int[][]isConnected,int i){
if(i>=isConnected.length){
return;
}
isConnected[i][i]=-1;
for(int j=0;j<isConnected[i].length;++j){
if(isConnected[i][j]==1&&i!=j&&isConnected[i][j]>0){
isConnected[i][j]=-1;
isConnected[j][i]=-1;
find(isConnected,j);
}
}
}
}
第四题:——深度优先搜索
给你一个二叉树的根节点 root ,树中每个节点都存放有一个 0 到 9 之间的数字。
每条从根节点到叶节点的路径都代表一个数字:
例如,从根节点到叶节点的路径 1 -> 2 -> 3 表示数字 123 。
计算从根节点到叶节点生成的 所有数字之和 。
叶节点 是指没有子节点的节点。
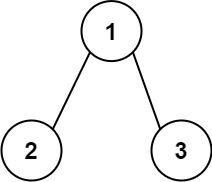
例如:12+13=25,其中1->2,1->3分别是两条根到叶的路径。
基本思路:判断当前节点是否是叶子节点,是就连接然后,将当前路径入顺序表中,否则连接节点,递归即可;最后遍历顺序表,对每条路径转换求和即可。
class Solution {
public int sumNumbers(TreeNode root) {
List<String>list=new ArrayList<>();
load(root,"",list);
int sum=0;
for(String s:list){
sum+=Integer.parseInt(s);
}
return sum;
}
public void load(TreeNode root,String str,List<String>list){
if(root==null){
return;
}
if(root.left==null&&root.right==null){
str+=(root.val+"");
list.add(str);
return;
}
str+=(root.val+"");
load(root.left,str,list);
load(root.right,str,list);
}
}
今天状态不太好,写了好久,但是,坚持就是胜利!!!!!!!!!