目录
一、实验目的
1、学习并掌握函数impz,dlsim和conv的使用;
2、充分理解系统特征根对系统时域特性的影响;
3、验证不同输入信号对系统零状态响应的影响,系统特征根对系统零状态响应的影响。
二、实验原理
LTI离散系统数学模型为
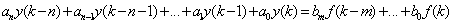
(1)离散系统的冲激响应h(k)的求取可调用函数impz(b, a)实现。其中a=[a2 a1 a0]是响应y侧系数向量,b=[b2 b1 b0]是激励f侧系数向量。
(2) 离散系统的零状态响应yzs(k)的可调用函数dlsim(b, a, f,)实现。其中f是激励向量,a、b向量同上。
(3)离散系统的零状态响应yzf(k)可以通过激励f(k)与单位冲激响应的卷积求解,调用conv(f, h)实现。
1、求离散系统的单位冲激和单位阶跃响应,matlab里用impz()、dstep()函数实现
(1)impz
功能:求解离散系统的冲激响应。
调用格式:
[h,k]=impz(b,a);求解离散系统的冲激响应h,取样点数为缺省值。
[h,k]=impz(b,a,n);求解离散系统的冲激响应h,取样点数由n确定。
impz(b,a);在当前窗口用stem(t,h)函数绘图。
(2)dstep
功能:求解离散系统的阶跃响应。
调用格式:
[h,k]=dstep(b,a);求解数字系统的阶跃响应h,取样点数为缺省值。
[h,k]=dstep(b,a,n);求解数字系统的阶跃响应h,取样点数由n确定。
dstep(b,a);在当前窗口用stairs(t,h)函数出图。
2、零状态响应
(1)fIlter
在MATLAB中,函数filter可以用来对差分方程在指定时间范围内的输入序列所产生的响应进行求解,该函数调用方法如下
y=filter(b,a,x)
其中,x为输入的离散序列,y为输出的离散序列,y的长度与x的长度一样,b与a
分别为差分方程右端与左端的系数向量
例1: 已知y(k)-0.35y(k-1)+1.5y(k-2)=f(k)+f(k-1),f(k)=((1/2)k)ɛ(k),其中ɛ(k)代表阶跃序列
a=[1 -0.35 1.5]; %方程左端的系数向量
b=[1 1]; %方程右端的系数向量
t=0:20; %指定时间序列
x=(1/2).^n; %输入激励
y=filter(b,a,x); %求解零状态响应
subplot(1,2,1)
stem(t,x)
title('输入序列')
grid on
xlabel('n')
ylabel('h(n)')
subplot(1,2,2)
stem(t,y)
xlabel('n')
ylabel('h(n)')
title('响应序列')
grid on
运行结果如图:

(2)dlsim
求取离散系统的零状态响应
调用格式:
y=dlsim(b,a,f) 或y=dlsim(sys,f)
f是系统输入信号向量,sys是LTI系统模型,表示差分方程。其调用格式
sys = tf (b,a)
3、卷积和运算
在MATLAB中,conv函数除了用于计算连续时间系统的卷积积分外,他还可以用于计
算离散序列的卷积和,其调用形式为
y=conv(f,h)
其中,f,h分别为待卷积的两个序列的向量表示,y是卷积结果。向量y的长度为向量f、h
的长度之和减1,即length(y)=length(f)+length(h)-1
x=[1,3,5,7]; %序列x
y=[1,1,1,1]; %序列y
z=conv(x,y) %求两个序列的卷积和
subplot(1,3,1);
stem(0:length(x)-1,x);
ylabel('x[n]');
xlabel('n');grid on
subplot(1,3,2)
stem(0:length(y)-1,y);
ylabel('y[n]');
xlabel('n');grid on
subplot(1,3,3)
stem(0:length(z)-1,z);
ylabel('z[n]');
xlabel('n')
grid on
运行结果如图:

例3:LTI差分方程y(k-2)-0.7y(k-1)+0.1y(k)=7f(k-2)-2f(k-1),激励为fk)=ε(k) 的零状态响应
(1)利用impz函数获得单位函数响应h(k),并绘制单位冲激函数响应的波形图;
(2)利用dlsim函数获得零状态响应yzs(k),并绘制零状态响应的波形图;
(3)利用卷积分析法求得零状态响应yzs(k),并绘制零状态响应的波形图;
b=[7,-2];a=[1,-0.7,0.1]
h=impz(b,a);
subplot(3,1,1)aa
stem(h);
title('单位冲激响应');
f=ones(1,16);
y1=dlsim(b,a,f)
subplot(3,1,2)
stem(y1);
title('零状态响应');
y2=conv(h,f) %卷积法求零状态响应
subplot(3,1,3)
stem(y2);
title('零状态响应')
运行结果如图:

三、 实验内容
1、已知f=[2,0,4;k=0,1,2],h=[1,3,0,2;k=1,2,3,4],编写matlab实现求y=f*h,并画出卷积的图形,验证卷积的性质。
程序如下:
f=[2,0,4];
h=[1,3,0,2];
z=conv(f,h)
subplot(1,3,1);
stem(0:length(f)-1,f);
title('f')
ylabel('f[k]');
xlabel('k');
grid on
subplot(1,3,2)
stem(1:length(h),h);
title('h')
ylabel('h[k]');
xlabel('k');grid on
subplot(1,3,3)
stem(1:length(z),z);
title('y')
ylabel('y[k]');
xlabel('k')
grid on
运行结果如下:

2、已知LTI离散系统差分方程为y(k-2)-y(k-1)-2y(k)=f(k),激励为 f (k)=ε(k),求零状态响应
(1)利用impz函数获得单位响应;
(2)利用dlsim函数求取零状态响应;
(3)用卷积分析法计算其零状态响应;要求:在一个图形窗口里以3个子图形式绘制单位响应和两种方法得到的零状态响应的波形。
程序如下:
b=[1];a=[1,-1,-2]
h=impz(b,a);
subplot(3,1,1)
stem(h);
title('单位冲激响应');
f=ones(1,16);
y1=dlsim(b,a,f)
subplot(3,1,2)
stem(y1);
title('零状态响应');
y2=conv(h,f) %卷积法求零状态响应
subplot(3,1,3)
stem(y2);
title('零状态响应')
运行结果如下:

(4)改变系统的a系数矩阵,分别画出波形图,分析单位响应和零状态响应时域波形的变化情况,a系数向量分别取如下取值讨论。
a=[1 -0.7 0.1],a=[1 0.7 0.1] a=[1 -1 0],a=[1 1 0] a=[1 -2 1],a=[1 2 1],a=[1 -2 1.5]
运行结果如下:

表 1

表 2

表 3

表 4

表 5

表 6

表 7
思考:
单位函数响应是增长型,衰减型,还是等幅型,是由a系数矩阵决定,b系数矩阵决定,还是由a,b系数矩阵共同决定?单位函数响应是否振荡又是由谁来决定的?(提示:在一个复平面中画出各特征根的位置,讨论特征根分别在单位圆内,单位圆上,单位圆外单位函数响应的模式;特征根为实数和复数时,单位函数响应的模式。)
四、 实验报告要求
1.简述实验目的和实验原理;
2.写出其对应的matlab程序;
3.计算相应的冲激响应、零状态响应及卷积积分的理论值,并与实验结果进行比较。
4.上机调试程序的方法及实验中的心得体会。
通过此次实验,我了解了卷积在Matlab中计算方法,学会了计算单位脉冲响应的方法。求系统的脉冲响应由两步组成:
①由 y(n)=x(n)*h(n)求出y(n)在MATLAB中用conv (x,h)实现
②用filter(b,a,x)求出单位脉冲响应