【LeetCode126】-单词接龙 II

方法一

实现思路

实现代码(超时)

//
struct Qitem{
    
    
    string value;
    int parent;
    int step;
    Qitem(string value,int parent,int step):value(value),parent(parent),step(step){
    
    ;}
};

class Solution {
    
    
public:
    bool isLink(string s1,string s2){
    
    
        int sum=0;
        for(int i=0;i<s1.size();i++){
    
    
            if(s2[i]!=s1[i])
                sum++;
        }
        return sum==1;
    }
    void getGraph(string beginWord,string endWord,vector<string> &wordList,map<string,vector<string>> &graph){
    
    
        bool has_begin=false;
        for(int i=0;i<wordList.size();i++){
    
    
            if(wordList[i]==beginWord)
                has_begin=true;
        }
        for(int i=0;i<graph.size();i++){
    
    
            vector<string> s;
            graph[wordList[i]]=s;
        }
        if(!has_begin){
    
     
            vector<string> s;
            graph[beginWord]=s;
        }
        for(int i=0;i<wordList.size();i++){
    
    //为了兼容建立beginWord的边，所以使用<wordList.size()
            for(int j=i+1;j<wordList.size();j++){
    
    
                if(isLink(wordList[i],wordList[j])){
    
    
                    graph[wordList[i]].push_back(wordList[j]);
                    graph[wordList[j]].push_back(wordList[i]);
                }
            }
            if(!has_begin&&isLink(beginWord,wordList[i])){
    
    
                graph[beginWord].push_back(wordList[i]);//只需要从头到别的边即可，因为是从头开始遍历的
            }
        }
    }
    void BFS(string beginWord, string endWord,vector<Qitem> &q,map<string,vector<string>>  &graph,map<string,int> &vis,vector<int> &end_pos){
    
    
        q.push_back(Qitem(beginWord,-1,1));
        int front=0;
        int min_step=0;
        while(front<q.size()){
    
    
            Qitem item=q[front];
            int step=item.step;
            string w=item.value;
            // cout<<step<<endl;
            if(min_step&&step>min_step) {
    
      
                break;
            }
            if(w==endWord){
    
    
                min_step=step;
                cout<<min_step<<endl;
                end_pos.push_back(front);
            }
            for(int i=0;i<graph[w].size();i++){
    
    
                string nw=graph[w][i];
                if(!vis.count(nw)||step+1==vis[nw]){
    
    
                    vis[nw]=step+1;
                    q.push_back(Qitem(nw,front,step+1));
                }
            }
            front++;
        }
    }
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    
    
        vector<vector<string>> re;
        bool flag=false;
        for(int i=0;i<wordList.size();i++){
    
    
            if(wordList[i]==endWord) flag=true;
        }
        if(!flag) return re;

        map<string,vector<string>>  graph;
        getGraph(beginWord,endWord,wordList,graph);

        vector<Qitem> q;
        map<string,int> vis;
        vector<int> end_pos;
        BFS(beginWord,endWord,q,graph,vis,end_pos);
        cout<<"lai"<<endl;
        for(int i=0;i<end_pos.size();i++){
    
    
            vector<string> path;
            int index=end_pos[i];
            while(index!=-1){
    
    
                path.push_back(q[index].value);
                index=q[index].parent;
            }
            vector<string> tpath;
            for(int j=int(path.size())-1;j>=0;j--){
    
    
                tpath.push_back(path[j]);
            }
            re.push_back(tpath);
        }
        return re; 
    }
};

提交结果及分析

超时，估计是BFS搜索空间过于庞大

方法二

方法2.1

实现思路
reference：花花酱题解

总体的思路：
和【LeetCode127】-单词接龙相同，都是进行宽度优先搜索，对于单词的每一位遍历换成26个字母

BFS搜索路径，使用parent的set来保存多条路径
再利用DFS递归的方法遍历出所有路径

允许多条路径，可以又多个父亲到达同一个节点，且该节点位置层级不变，注意在这里面当一个单词遍历完之后是要从字典中删除，删除的原因是之后不可能再遍历比当前更短的路径长度了

注意 在具体搜索的里面，当word不再dict时break的放置顺序很重要：
break必须放在判断w为endWord和w是否为一种多条路径的可能之前，原因在于endWord一开始就移除来dict，每一次字典里的单词第一次出现后就会从字典中删除

Q: 为什么当遍历到endWord的时候，就可以考虑遍历结束了
A: 因为该算法属于BFS，而且路径的长度均为1，所以后续的路径长度一定会增加

实现代码

class Solution {
    
    
public:
    //使用递归遍历的方法
    void getPath(string word,string &beginWord,string &endWord,unordered_map<string,set<string>> &parent,vector<string> &cur,vector<vector<string>> &re){
    
    
        if(word==beginWord){
    
    
            re.push_back(vector<string>(cur.rbegin(),cur.rend()));
        }
        //对于每一个单词枚举出其不同parent的结果
        for(string s:parent[word]){
    
    
            cur.push_back(s);
            getPath(s,beginWord,endWord,parent,cur,re);
            cur.pop_back();
        }
    }
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    
    
        vector<vector<string>> re;
        unordered_set<string> dict(wordList.begin(),wordList.end());
        if(dict.count(endWord)==0) return re;
        dict.erase(beginWord);

        //multipath save
        unordered_map<string,int> steps{
    
    {
    
    beginWord,1}};
        unordered_map<string,set<string>> parent;//保证不会压入重复值所以使用set来处理

        queue<string> q;
        q.push(beginWord);
        bool found=false;
        int len=wordList[0].length();
        int step=0;
        while(!q.empty()&&!found){
    
    //当队列为空或者已经搜索到endendWord就停止
            step++;
            
            //遍历队列中所含有的元素
            int size=q.size();//先保存队列的大小，由于后续可能大小会有所改变
            for(int k=0;k<size;k++){
    
    
                string w=q.front();q.pop();
                string bw=w;//保留之前的字符串
                for(int i=0;i<len;i++){
    
    
                    char ch=w[i];
                    for(int j=0;j<26;j++){
    
    
                        if('a'+j==ch) continue;

                        w[i]='a'+j;
                        if(w==endWord){
    
    
                            parent[w].insert(bw);
                            found=true;
                        }
                        

                        if(dict.count(w)&&!steps.count(w)) {
    
    //为减少不必要的结果保存，保证是字典中的字符串
                            steps[w]=steps[bw]+1;
                            // cout<<steps[w]<<endl;
                            set<string> s;
                            s.insert(bw);
                            parent[w]=s;
                        }
                        else if(steps.count(w)){
    
    //这种情况下不需要考虑是字典中的情况
                            //这里的代码是为了保证可以保存多条路径
                            if(steps[w]==steps[bw]+1)
                                parent[w].insert(bw);
                        }

                        if(!dict.count(w)) continue;

                        dict.erase(w);
                        q.push(w);
                    }
                    w[i]=ch;//恢复之前的字符，以便下次进行修改遍历
                }
            }
        }
        if(found){
    
    
            vector<string> cur{
    
    endWord};
            //
            getPath(endWord,beginWord,endWord,parent,cur,re);
        }
        return re;
    }

};

huahua酱实现的代码

// Author: Huahua
// Running Time: 216 ms (better than 65.42%)
class Solution {
    
    
public:
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    
    
        
        unordered_set<string> dict(wordList.begin(), wordList.end());        
        if (!dict.count(endWord)) return {
    
    };
        dict.erase(beginWord);
        dict.erase(endWord);
        
        unordered_map<string, int> steps{
    
    {
    
    beginWord, 1}};
        unordered_map<string, vector<string>> parents;
        queue<string> q;
        q.push(beginWord);
        
        vector<vector<string>> ans;
        
        const int l = beginWord.length();
        int step = 0;        
        bool found = false;
        
        while (!q.empty() && !found) {
    
    
            ++step;            
            for (int size = q.size(); size > 0; size--) {
    
    
                const string p = q.front(); q.pop();
                string w = p;
                for (int i = 0; i < l; i++) {
    
    
                    const char ch = w[i];
                    for (int j = 'a'; j <= 'z'; j++) {
    
    
                        if (j == ch) continue;
                        w[i] = j;
                        if (w == endWord) {
    
    
                            parents[w].push_back(p);
                            found = true;
                        } else {
    
    
                            // Not a new word, but another transform
                            // with the same number of steps
                            if (steps.count(w) && step < steps.at(w))
                                parents[w].push_back(p);
                        }
                        
                        if (!dict.count(w)) continue;
                        dict.erase(w);
                        q.push(w);
                        steps[w] = steps.at(p) + 1;
                        parents[w].push_back(p);
                    }
                    w[i] = ch;
                }
            }
        }
        
        if (found) {
    
    
            vector<string> curr{
    
    endWord};
            getPaths(endWord, beginWord, parents, curr, ans);
        }
    
        return ans;
    }
private:
    void getPaths(const string& word, 
                  const string& beginWord, 
                  const unordered_map<string, vector<string>>& parents,
                  vector<string>& curr,
                  vector<vector<string>>& ans) {
    
            
        
        if (word == beginWord) {
    
    
            ans.push_back(vector<string>(curr.rbegin(), curr.rend()));
            return;
        }
        
        for (const string& p : parents.at(word)) {
    
    
            curr.push_back(p);
            getPaths(p, beginWord, parents, curr, ans);
            curr.pop_back();
        }        
    }
};

这里不会重复的原因，在于第一次访问后dict会删除该word，之后到下一个红方框之前会break

方法二基础解法提交结果及分析

方法2.2

实现思路：
方法2.1是当该单词可以出现重复路径的情况下，可以考虑将该元素压入队列中，但其实可能会出现一个元素重复压入多次，所尝试使用set来进行优化

两个代码中的不同点：

1. 方法2.1使用队列，先代码使用set实现一样的存储同一层单词的作用
   好处：使用set，可以删除重复的元素，避免了不必要的搜索

2. 方法2.1使用一个队列，现代码使用两个set
   （1）原先的情况下，遍历当前一层队列中的所有元素，需要记录一下这一层队列中元素的个数，否则在后续队列添加元素的时候会导致队列的个数发生变化
   （2）现在这种情况不需要记录，只要把新添加的元素放在另一个set中即可，注意两个set在替换的时候，不适用的set要清空

3. 方法2.2基础代码存储的是父节点数组，现代码存储路径使用的是孩子节点数组

整体思路
用set来模拟队列功能，遍历set中的数据，并将它们从set中删除，针对set中的字符串遍历字符串的每一位并将其更改为a～z中的一位，判断更改后的字符串是否再字典里且当前没遍历到endWord，就将该字符串压入到set中，同时存储children信息
最后路径的获取使用DFS遍历得到

注意
1.set元素遍历之前从字典里清空
2.遍历字符串新的一位时，记得将之前改变的复原
3.可以使用两个set替换来完成遍历功能，另一个不使用的set记得清空

实现代码

class Solution {
    
    
public:
    void getPath(string &word,string &endWord,vector<string> &curr,unordered_map<string,set<string>> &children,vector<vector<string>> &re){
    
    
        if(word==endWord){
    
    
            re.push_back(curr);
            return;
        }
        if(!children.count(word)){
    
    
            return;
        }
        for(string s:children[word]){
    
    
            curr.push_back(s);
            getPath(s,endWord,curr,children,re);
            curr.pop_back();
        }
    }
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    
    
        vector<vector<string>> re;
        unordered_set<string> dict(wordList.begin(),wordList.end());
        if(!dict.count(endWord)) return re;
        dict.erase(endWord);
        set<string> q{
    
    beginWord};
        unordered_map<string,set<string>> children;
        set<string> ans_pos;
        bool found=false;
        int len=wordList[0].length();

        while(!q.empty()&&!found){
    
    
            cout<<q.size()<<endl;
            for(string s:q){
    
    
                dict.erase(s);
            }
            set<string> p;
            for(string w:q){
    
    
                string bw=w;
                for(int i=0;i<len;i++){
    
    
                    char ch=w[i];
                    for(int j=0;j<26;j++){
    
    
                        w[i]='a'+j;
                        if(w==bw) continue;
                        if(w==endWord){
    
    
                            children[bw].insert(w);
                            found=true;
                        }
                        if(dict.count(w)&&!found){
    
    
                            p.insert(w);
                            children[bw].insert(w);
                        }
                        if(!dict.count(w)) continue;
                        // cout<<w<<endl;
                    }
                    w[i]=ch;
                }
            }
            q.clear();
            std::swap(q,p);
            
        }
        if(found){
    
    
            vector<string> curr{
    
    beginWord};
            getPath(beginWord,endWord,curr,children,re);
        }
        return re;
    }
};

提交结果
超出时间限制了

超时的样例：

"aaaaaaaaaa"
"bccccccccb"
["aaaaaaaaaa","caaaaaaaaa","cbaaaaaaaa","daaaaaaaaa","dbaaaaaaaa","eaaaaaaaaa","ebaaaaaaaa","faaaaaaaaa","fbaaaaaaaa","gaaaaaaaaa","gbaaaaaaaa","haaaaaaaaa","hbaaaaaaaa","iaaaaaaaaa","ibaaaaaaaa","jaaaaaaaaa","jbaaaaaaaa","kaaaaaaaaa","kbaaaaaaaa","laaaaaaaaa","lbaaaaaaaa","maaaaaaaaa","mbaaaaaaaa","naaaaaaaaa","nbaaaaaaaa","oaaaaaaaaa","obaaaaaaaa","paaaaaaaaa","pbaaaaaaaa","qaaaaaaaaa","qbaaaaaaaa","raaaaaaaaa","rbaaaaaaaa","saaaaaaaaa","sbaaaaaaaa","taaaaaaaaa","tbaaaaaaaa","uaaaaaaaaa","ubaaaaaaaa","vaaaaaaaaa","vbaaaaaaaa","waaaaaaaaa","wbaaaaaaaa","xaaaaaaaaa","xbaaaaaaaa","yaaaaaaaaa","ybaaaaaaaa","zaaaaaaaaa","zbaaaaaaaa","bbaaaaaaaa","bdaaaaaaaa","bdbaaaaaaa","beaaaaaaaa","bebaaaaaaa","bfaaaaaaaa","bfbaaaaaaa","bgaaaaaaaa","bgbaaaaaaa","bhaaaaaaaa","bhbaaaaaaa","biaaaaaaaa","bibaaaaaaa","bjaaaaaaaa","bjbaaaaaaa","bkaaaaaaaa","bkbaaaaaaa","blaaaaaaaa","blbaaaaaaa","bmaaaaaaaa","bmbaaaaaaa","bnaaaaaaaa","bnbaaaaaaa","boaaaaaaaa","bobaaaaaaa","bpaaaaaaaa","bpbaaaaaaa","bqaaaaaaaa","bqbaaaaaaa","braaaaaaaa","brbaaaaaaa","bsaaaaaaaa","bsbaaaaaaa","btaaaaaaaa","btbaaaaaaa","buaaaaaaaa","bubaaaaaaa","bvaaaaaaaa","bvbaaaaaaa","bwaaaaaaaa","bwbaaaaaaa","bxaaaaaaaa","bxbaaaaaaa","byaaaaaaaa","bybaaaaaaa","bzaaaaaaaa","bzbaaaaaaa","bcbaaaaaaa","bcdaaaaaaa","bcdbaaaaaa","bceaaaaaaa","bcebaaaaaa","bcfaaaaaaa","bcfbaaaaaa","bcgaaaaaaa","bcgbaaaaaa","bchaaaaaaa","bchbaaaaaa","bciaaaaaaa","bcibaaaaaa","bcjaaaaaaa","bcjbaaaaaa","bckaaaaaaa","bckbaaaaaa","bclaaaaaaa","bclbaaaaaa","bcmaaaaaaa","bcmbaaaaaa","bcnaaaaaaa","bcnbaaaaaa","bcoaaaaaaa","bcobaaaaaa","bcpaaaaaaa","bcpbaaaaaa","bcqaaaaaaa","bcqbaaaaaa","bcraaaaaaa","bcrbaaaaaa","bcsaaaaaaa","bcsbaaaaaa","bctaaaaaaa","bctbaaaaaa","bcuaaaaaaa","bcubaaaaaa","bcvaaaaaaa","bcvbaaaaaa","bcwaaaaaaa","bcwbaaaaaa","bcxaaaaaaa","bcxbaaaaaa","bcyaaaaaaa","bcybaaaaaa","bczaaaaaaa","bczbaaaaaa","bccbaaaaaa","bccdaaaaaa","bccdbaaaaa","bcceaaaaaa","bccebaaaaa","bccfaaaaaa","bccfbaaaaa","bccgaaaaaa","bccgbaaaaa","bcchaaaaaa","bcchbaaaaa","bcciaaaaaa","bccibaaaaa","bccjaaaaaa","bccjbaaaaa","bcckaaaaaa","bcckbaaaaa","bcclaaaaaa","bcclbaaaaa","bccmaaaaaa","bccmbaaaaa","bccnaaaaaa","bccnbaaaaa","bccoaaaaaa","bccobaaaaa","bccpaaaaaa","bccpbaaaaa","bccqaaaaaa","bccqbaaaaa","bccraaaaaa","bccrbaaaaa","bccsaaaaaa","bccsbaaaaa","bcctaaaaaa","bcctbaaaaa","bccuaaaaaa","bccubaaaaa","bccvaaaaaa","bccvbaaaaa","bccwaaaaaa","bccwbaaaaa","bccxaaaaaa","bccxbaaaaa","bccyaaaaaa","bccybaaaaa","bcczaaaaaa","bcczbaaaaa","bcccbaaaaa","bcccdaaaaa","bcccdbaaaa","bccceaaaaa","bcccebaaaa","bcccfaaaaa","bcccfbaaaa","bcccgaaaaa","bcccgbaaaa","bccchaaaaa","bccchbaaaa","bccciaaaaa","bcccibaaaa","bcccjaaaaa","bcccjbaaaa","bccckaaaaa","bccckbaaaa","bccclaaaaa","bccclbaaaa","bcccmaaaaa","bcccmbaaaa","bcccnaaaaa","bcccnbaaaa","bcccoaaaaa","bcccobaaaa","bcccpaaaaa","bcccpbaaaa","bcccqaaaaa","bcccqbaaaa","bcccraaaaa","bcccrbaaaa","bcccsaaaaa","bcccsbaaaa","bccctaaaaa","bccctbaaaa","bcccuaaaaa","bcccubaaaa","bcccvaaaaa","bcccvbaaaa","bcccwaaaaa","bcccwbaaaa","bcccxaaaaa","bcccxbaaaa","bcccyaaaaa","bcccybaaaa","bccczaaaaa","bccczbaaaa","bccccbaaaa","bccccdaaaa","bccccdbaaa","bcccceaaaa","bccccebaaa","bccccfaaaa","bccccfbaaa","bccccgaaaa","bccccgbaaa","bcccchaaaa","bcccchbaaa","bcccciaaaa","bccccibaaa","bccccjaaaa","bccccjbaaa","bcccckaaaa","bcccckbaaa","bcccclaaaa","bcccclbaaa","bccccmaaaa","bccccmbaaa","bccccnaaaa","bccccnbaaa","bccccoaaaa","bccccobaaa","bccccpaaaa","bccccpbaaa","bccccqaaaa","bccccqbaaa","bccccraaaa","bccccrbaaa","bccccsaaaa","bccccsbaaa","bcccctaaaa","bcccctbaaa","bccccuaaaa","bccccubaaa","bccccvaaaa","bccccvbaaa","bccccwaaaa","bccccwbaaa","bccccxaaaa","bccccxbaaa","bccccyaaaa","bccccybaaa","bcccczaaaa","bcccczbaaa","bcccccbaaa","bcccccdaaa","bcccccdbaa","bccccceaaa","bcccccebaa","bcccccfaaa","bcccccfbaa","bcccccgaaa","bcccccgbaa","bccccchaaa","bccccchbaa","bccccciaaa","bcccccibaa","bcccccjaaa","bcccccjbaa","bccccckaaa","bccccckbaa","bccccclaaa","bccccclbaa","bcccccmaaa","bcccccmbaa","bcccccnaaa","bcccccnbaa","bcccccoaaa","bcccccobaa","bcccccpaaa","bcccccpbaa","bcccccqaaa","bcccccqbaa","bcccccraaa","bcccccrbaa","bcccccsaaa","bcccccsbaa","bccccctaaa","bccccctbaa","bcccccuaaa","bcccccubaa","bcccccvaaa","bcccccvbaa","bcccccwaaa","bcccccwbaa","bcccccxaaa","bcccccxbaa","bcccccyaaa","bcccccybaa","bccccczaaa","bccccczbaa","bccccccbaa","bccccccdaa","bccccccdba","bcccccceaa","bcccccceba","bccccccfaa","bccccccfba","bccccccgaa","bccccccgba","bcccccchaa","bcccccchba","bcccccciaa","bcccccciba","bccccccjaa","bccccccjba","bcccccckaa","bcccccckba","bcccccclaa","bcccccclba","bccccccmaa","bccccccmba","bccccccnaa","bccccccnba","bccccccoaa","bccccccoba","bccccccpaa","bccccccpba","bccccccqaa","bccccccqba","bccccccraa","bccccccrba","bccccccsaa","bccccccsba","bcccccctaa","bcccccctba","bccccccuaa","bccccccuba","bccccccvaa","bccccccvba","bccccccwaa","bccccccwba","bccccccxaa","bccccccxba","bccccccyaa","bccccccyba","bcccccczaa","bcccccczba","bcccccccba","bcccccccda","bcccccccdb","bcccccccea","bccccccceb","bcccccccfa","bcccccccfb","bcccccccga","bcccccccgb","bcccccccha","bccccccchb","bcccccccia","bcccccccib","bcccccccja","bcccccccjb","bcccccccka","bccccccckb","bcccccccla","bccccccclb","bcccccccma","bcccccccmb","bcccccccna","bcccccccnb","bcccccccoa","bcccccccob","bcccccccpa","bcccccccpb","bcccccccqa","bcccccccqb","bcccccccra","bcccccccrb","bcccccccsa","bcccccccsb","bcccccccta","bccccccctb","bcccccccua","bcccccccub","bcccccccva","bcccccccvb","bcccccccwa","bcccccccwb","bcccccccxa","bcccccccxb","bcccccccya","bcccccccyb","bcccccccza","bccccccczb","bccccccccb","aaaaaaaaaz","aaaaaaaabz","aaaaaaacbz","aaaaaaacbc","aaaaaadcbc","aaaaaedcbc","aaaaaedccc","aaaafedccc","aaaafecccc","aaaffecccc","aafffecccc","aaffcecccc","aaffcccccc","acffcccccc","acfccccccc","accccccccc","accccccccb"]

方法2.1和方法2.2的比较

在方法2.1中由于记录的是parent数据，所以需要多维护一个记录步数的数组
在方法2.2中由于记录的是children数据，不需要维护多的步数数字，只需要遍历这一层时保证，dict中先将它们删除掉不会重复访问，在a～z遍历到满足条件的children时直接存储即可，这样满足条件的原因也是在于由于时宽度优先搜索，这个孩子能现在遍历到说明肯定是最短的情形，这个孩子也会被压入大的遍历set中，按照程序的逻辑该孩子在dict会被删除，也就保证了不会再被访问到

方法2.3

使用双向宽度优先搜索的方法
实现代码

// Author: Huahua
// Running time: 129 ms (better than 80.67%)
class Solution {
    
    
public:
    vector<vector<string>> findLadders(string beginWord, string endWord, vector<string>& wordList) {
    
    
        vector<vector<string>> ans;
        unordered_set<string> dict(wordList.begin(), wordList.end());
        if (!dict.count(endWord)) return ans;
        dict.erase(endWord);        
        
        set<string> q1{
    
    beginWord},q2{
    
    endWord};
        unordered_map<string,vector<string>> children;
        bool found=false;
        bool reserve=false;
        int len=wordList[0].length();

        while(!q1.empty()&&!q2.empty()&&!found){
    
    
            
            if(q1.size()>q2.size()){
    
    
                std::swap(q1,q2);
                reserve=!reserve;
            }
            for (const string& w : q1)
                dict.erase(w);
            for (const string& w : q2)
                dict.erase(w);

            set<string> p;
            for(string w:q1){
    
    
                string bw=w;
                for(int i=0;i<len;i++){
    
    
                    char ch=w[i];
                    for(int j=0;j<26;j++){
    
    
                        w[i]='a'+j;
                        if(w==bw) continue;
                        if(q2.count(w)){
    
    
                            found=true;
                            if(reserve){
    
    
                                children[w].push_back(bw);
                            }else{
    
    
                                children[bw].push_back(w);
                            }
                            
                        }
                        if(!found&&dict.count(w)){
    
    
                            p.insert(w);
                            if(reserve){
    
    
                                children[w].push_back(bw);
                            }else{
    
    
                                children[bw].push_back(w);
                            }
                        }
                        if(!dict.count(w)) continue;
                        // cout<<w<<endl;
                            
                        
                    }
                    w[i]=ch;
                }
            }
            std::swap(q1,p);
            
        }
        if (found) {
    
    
            vector<string> path{
    
    beginWord};
            getPaths(beginWord, endWord, children, path, ans);
        }
        
        return ans;
    }
private:
    void getPaths(const string& word, 
                  const string& endWord,                   
                  const unordered_map<string, vector<string>>& children,
                  vector<string>& path, 
                  vector<vector<string>>& ans) {
    
    
        if (word == endWord) {
    
    
            ans.push_back(path);
            return;
        }
        
        const auto it = children.find(word);
        if (it == children.cend()) return;
        
        for (const string& child : it->second) {
    
    
            path.push_back(child);
            getPaths(child, endWord, children, path, ans);
            path.pop_back();
        }
    }    
};

提交结果
超时

方法二的总结：

利用parent数组存储进行的宽度优先搜索不超时，而使用children宽度优先搜索的代码出现了超时，可能是利用parent的节点时候有dict的限制和步数的限制，而children数组没那么多限制吧（不确定）

总结

需要记住的知识点：
1.宽度优先搜索的路径保存，以及多条路径的保存
2.将数组内容进行反转

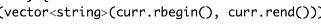
需要记住的代码
//这种遍历的方法可以考虑尝试应用在一个节点的到达有多种方法

   void getPath(string word,string &beginWord,string &endWord,unordered_map<string,set<string>> &parent,vector<string> &cur,vector<vector<string>> &re){
       if(word==beginWord){
           re.push_back(vector<string>(cur.rbegin(),cur.rend()));
       }
       //对于每一个单词枚举出其不同parent的结果
       for(string s:parent[word]){
           cur.push_back(s);
           getPath(s,beginWord,endWord,parent,cur,re);
           cur.pop_back();
       }
   }

tip：
在使用函数的参数的时候可以使用常引用
好处：可以发现错误，例：在使用vector的at时候，如果没有常引用会创建一个，从而出现了错误