有关模态逻辑的知识请看模态逻辑入门笔记,有关证据理论的知识请看证据理论入门笔记。本文主要记录我对文献[1]的理解,文献[2]介绍了一种基于多值映射 (Multivalued mapping) 解释证据理论的方法,多值映射类似模态理论中的关系 R R R。
符号定义
- M = < W , R , V > M=<W,R,V> M=<W,R,V>,模态逻辑的模型 M M M,模态逻辑采用系统 T 或更强的模态逻辑系统,即 R R R 满足反身性 (reflexive),每个可能世界能够到达自身。
- ∣ ∣ p ∣ ∣ M ||p||^M ∣∣p∣∣M,命题 p p p 的真集 (Truth set),即 ∣ ∣ p ∣ ∣ M = { w ∣ w ∈ W ∧ V ( p , w ) = T } ||p||^M=\{w|w\in W\wedge V(p,w)=T\} ∣∣p∣∣M={ w∣w∈W∧V(p,w)=T}。
- ∣ A ∣ |A| ∣A∣,集合 A A A 的基数,即集合 A A A 中元素的个数。例如, A = { 1 , 2 , 3 } , ∣ A ∣ = 3 A=\{1,2,3\},|A|=3 A={ 1,2,3},∣A∣=3。
- X X X,证据理论的辨识架构。
- e A e_A eA,一个命题,表示一个给定的研究元素被分类到集合 A A A 中。
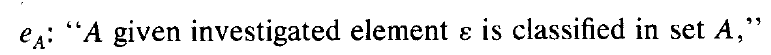
e A = ⋁ x ∈ A e { x } , ∀ A ≠ ∅ ; e ∅ = ⋀ x ∈ X ¬ e { x } e_A=\bigvee_{x\in A}e_{\{x\}},\forall A \neq \emptyset;\qquad e_\emptyset=\bigwedge_{x\in X}\neg e_{\{x\}} eA=x∈A⋁e{ x},∀A=∅;e∅=x∈X⋀¬e{ x}
证据理论的模态逻辑解释
- 信任函数: B e l ( A ) = ∑ B ⊆ A m ( B ) = ∣ ∣ ∣ □ e A ∣ ∣ M ∣ ∣ W ∣ Bel(A)=\sum_{B\subseteq A}m(B)=\frac{\big\lvert||\square e_A||^M\big\rvert}{|W|} Bel(A)=B⊆A∑m(B)=∣W∣∣∣∣∣□eA∣∣M∣∣
- 似然函数: P l ( A ) = ∑ B ∩ A ≠ ∅ m ( B ) = ∣ ∣ ∣ ◊ e A ∣ ∣ M ∣ ∣ W ∣ Pl(A)=\sum_{B\cap A\neq\emptyset}m(B)=\frac{\big\lvert||\Diamond e_A||^M\big\rvert}{|W|} Pl(A)=B∩A=∅∑m(B)=∣W∣∣∣∣∣◊eA∣∣M∣∣
- 基本概率分配函数: m ( A ) = ∣ ∣ ∣ E A ∣ ∣ M ∣ ∣ W ∣ m(A)=\frac{\big\lvert||E_A||^M\big\rvert}{|W|} m(A)=∣W∣∣∣∣∣EA∣∣M∣∣ E A = □ e A ∧ ( ⋀ B ⊂ A ( ¬ ( □ e B ) ) ) E_A=\square e_A \wedge \Big(\bigwedge_{B\subset A}(\neg(\square e_B))\Big) EA=□eA∧(B⊂A⋀(¬(□eB)))
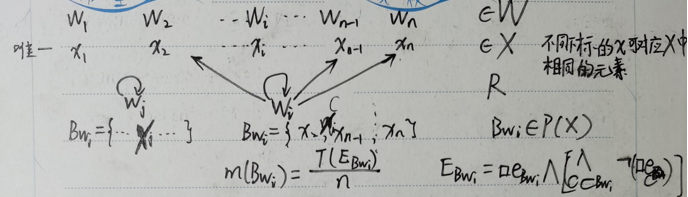
下面解释上面几个公式(可以参考下图)。首先,假设在每一个可能世界 w w w 中,有且仅有一个 x ∈ W x\in W x∈W 使命题 e { x } e_{\{x\}} e{
x} 为真 (Singleton Valuation Assumption),我称之为可能世界 w w w 对应的 x x x。 w ′ w' w′ 是从一个 w w w 能够到达的可能世界(可能有好几个 w ′ w' w′), w ′ w' w′ 对应的 x x x 构成集合 B B B,我称之为 w w w 对应的集合 B B B。
接下来,有一类 w w w 的集合,其中 w w w 对应的集合 B B B 是集合 A A A 的子集,即有 ( ∀ w ′ ) ( w R w ′ ⊃ V ( e A , w ′ ) = T ) (\forall w') (wRw'\supset V(e_A,w')=T) (∀w′)(wRw′⊃V(eA,w′)=T),则 V ( □ e A , w ) = T V(\square e_A,w)=T V(□eA,w)=T,这类 w w w 的集合即为 ∣ ∣ □ e A ∣ ∣ M ||\square e_A||^M ∣∣□eA∣∣M。
还有一类 w w w 的集合,其中的任意一个 w w w 能到达的可能世界 w ′ w' w′, w ′ w' w′ 对应的 x x x 构成的集合 B B B 包含集合 A A A,这类 w w w 的集合为 ∣ ∣ ⋀ x ∈ A ◊ e { x } ∣ ∣ M ||\bigwedge_{x\in A}\Diamond e_{\{x\}}||^M ∣∣⋀x∈A◊e{
x}∣∣M。
另一类 w w w 的集合,其中 w w w 对应的集合 B B B 与集合 A A A相交不为空集,即 B ∩ A ≠ ∅ B\cap A \neq \emptyset B∩A=∅,则有 ( ∃ w ′ ) ( w R w ′ ∧ V ( e A , w ′ ) = T ) (\exist w') (wRw'\wedge V(e_A,w')=T) (∃w′)(wRw′∧V(eA,w′)=T),这类 w w w 的集合即为 ∣ ∣ ◊ e A ∣ ∣ M ||\Diamond e_A||^M ∣∣◊eA∣∣M。
定义一个集合 B w = { x ∈ X ∣ ( ∃ w ′ ) ( w R w ′ ∧ V ( e { x } , w ′ ) = T ) } B_w=\{x\in X\big|(\exist w')(wRw'\wedge V(e_{\{x\}},w')=T)\} Bw={
x∈X∣∣(∃w′)(wRw′∧V(e{
x},w′)=T)},其实就是上述 3 中的集合 A A A,对于每一个可能世界 w w w,这样的集合有且只有一个,不同的 w w w 可以有相同的 B w B_w Bw, B w B_w Bw 由所有 w w w 可以到达的 w ′ w' w′ 对应的 x x x 构成。
由上述分析可以看出,可能世界 w w w 对应的集合 B B B 和集合 A A A 之间的关系是符合经典 DS 证据理论的,这样也就能更好的理解上述公式。
Example

证据理论的模态逻辑解释的完整性 (Completeness)
对于每一个由理数构成的基本概率分配函数,都存在一个系统 T 的模态逻辑模型 M M M 能推导出该基本概率分配函数。看例子怎么找这个模型 M M M 。
Example
